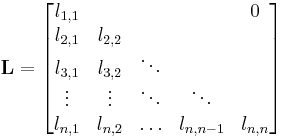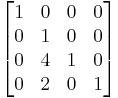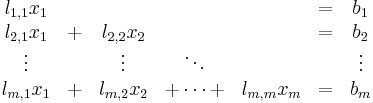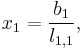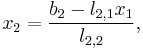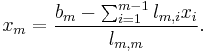Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero. A matrix which is similar to a triangular matrix is called triangularizable.
Because matrix equations with triangular matrices are easier to solve they are very important in numerical analysis. The LU decomposition gives an algorithm to decompose any invertible matrix A into two triangular factors: a normed lower triangle matrix L and an upper triangle matrix U.
Contents |
Description
A matrix of the form
is called lower triangular matrix or left triangular matrix, and analogously a matrix of the form
is called upper triangular matrix or right triangular matrix.
The standard operations on triangular matrices conveniently preserve the triangular form: the sum and product of two upper triangular matrices is again upper triangular. The inverse of an upper triangular matrix is also upper triangular, and of course we can multiply an upper triangular matrix by a constant and it will still be upper triangular. This means that the upper triangular matrices form a subalgebra of the ring of square matrices for any given size. The analogous result holds for lower triangular matrices. Note, however, that the product of a lower triangular with an upper triangular matrix does not preserve triangularity.
Special forms
Strictly triangular matrix
A triangular matrix with zero entries on the main diagonal is strictly upper or lower triangular. All strictly triangular matrices are nilpotent, and they form a nilpotent Lie algebra, denoted 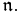 Strictly upper triangular matrices are the derived Lie algebra of the Lie algebra
Strictly upper triangular matrices are the derived Lie algebra of the Lie algebra 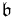 of all upper triangular matrices; symbolically,
of all upper triangular matrices; symbolically, ![\mathfrak{n} = [\mathfrak{b},\mathfrak{b}].](/2012-wikipedia_en_all_nopic_01_2012/I/9b7f9841e00a0c333de3b7a9593e962a.png) Strictly upper triangular matrices are the Lie algebra of the Lie group of unitriangular matrices.
Strictly upper triangular matrices are the Lie algebra of the Lie group of unitriangular matrices.
In fact, by Engel's theorem, any nilpotent Lie algebra is conjugate to a subalgebra of the strictly upper triangular matrices: a nilpotent Lie algebra is simultaneously strictly upper triangularizable.
Unitriangular matrix
If the entries on the main diagonal are 1, the matrix is called (upper or lower) unitriangular. All unitriangular matrices are unipotent. Other names used for these matrices are unit (upper or lower) triangular (of which "unitriangular" might be a contraction), or normed upper/lower triangular (very rarely used). However a unit triangular matrix is not the same as the unit matrix, and a normed triangular matrix has nothing to do with the notion of matrix norm.
Unitriangular matrices form a Lie group, whose Lie algebra is the strictly upper triangular matrices.
Gauss matrix
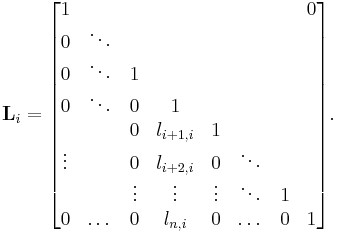
A Gauss matrix is a special form of a unitriangular matrix, where all of the off-diagonal entries are zero, except for the entries in one column. Such a matrix is also called atomic upper/lower triangular or Gauss transformation matrix. So an atomic lower triangular matrix is of the form
The inverse of an atomic triangular matrix is again atomic triangular. Indeed, we have
i.e., the single column of off-diagonal entries are replaced in the inverse matrix by their additive inverses.
Special properties
A matrix which is simultaneously upper and lower triangular is diagonal. The identity matrix is the only matrix which is both upper and lower unitriangular.
A matrix which is simultaneously triangular and normal is also diagonal. This can be seen by looking at the diagonal entries of A*A and AA*, where A is a normal, triangular matrix.
The transpose of an upper triangular matrix is a lower triangular matrix and vice versa.
The determinant of a triangular matrix equals the product of the diagonal entries. Since for any triangular matrix A the matrix 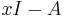 , whose determinant is the characteristic polynomial of A, is also triangular, the diagonal entries of A in fact give the multiset of eigenvalues of A (an eigenvalue with multiplicity m occurs exactly m times as diagonal entry).[1]
, whose determinant is the characteristic polynomial of A, is also triangular, the diagonal entries of A in fact give the multiset of eigenvalues of A (an eigenvalue with multiplicity m occurs exactly m times as diagonal entry).[1]
The variable L is commonly used for lower triangular matrix, standing for lower/left, while the variable U or R is commonly used for upper triangular matrix, standing for upper/right.
Many operations can be performed more easily on triangular matrices than on general matrices. Notably matrix inversion (when possible) can be done by back substitution, avoiding the complications of general Gaussian elimination.
The inverse of a triangular matrix is also triangular.
The product of two lower triangular matrices produces a lower triangular matrix.
The product of two upper triangular matrices produces an upper triangular matrix.
Triangularisability
A matrix that is similar to a triangular matrix is referred to as triangularisable. Abstractly, this is equivalent to stabilising a flag: upper triangular matrices are precisely those that preserve the standard flag, which is given by the standard ordered basis  and the resulting flag
and the resulting flag  All flags are conjugate (as the general linear group acts transitively on bases), so any matrix that stabilises a flag is similar to one that stabilises the standard flag.
All flags are conjugate (as the general linear group acts transitively on bases), so any matrix that stabilises a flag is similar to one that stabilises the standard flag.
Any complex square matrix is triangularisable.[1] In fact, a matrix A over a field containing all of the eigenvalues of A (for example, any matrix over an algebraically closed field) is similar to a triangular matrix. This can be proven by using induction on the fact that A has an eigenvector, by taking the quotient space by the eigenvector and inducting to show that A stabilises a flag, and is thus triangularisable with respect to a basis for that flag.
A more precise statement is given by the Jordan normal form theorem, which states that in this situation, A is similar to an upper triangular matrix of a very particular form. The simpler triangularization result is often sufficient however, and in any case used in proving the Jordan normal form theorem.[1][2]
In the case of complex matrices, it is possible to say more about triangularisation, namely, that any square matrix A has a Schur decomposition. This means that A is unitarily equivalent (i.e. similar, using a unitary matrix as change of basis) to an upper triangular matrix; this follows by taking an Hermitian basis for the flag.
Simultaneous triangularisability
A set of matrices  are said to be simultaneously triangularisable if there is a basis under which they are all upper triangular; equivalently, if they are upper triangularizable by a single similarity matrix P. Such a set of matrices is more easily understood by considering the algebra of matrices it generates, namely all polynomials in the
are said to be simultaneously triangularisable if there is a basis under which they are all upper triangular; equivalently, if they are upper triangularizable by a single similarity matrix P. Such a set of matrices is more easily understood by considering the algebra of matrices it generates, namely all polynomials in the 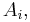 denoted
denoted ![K[A_1,\ldots,A_k].](/2012-wikipedia_en_all_nopic_01_2012/I/d70ba709035d6d99a45eb125201a2e96.png) Simultaneous triangularizability means that this algebra is conjugate into the Lie subalgebra of upper triangular matrices, and is equivalent to this algebra being a Lie subalgebra of a Borel subalgebra.
Simultaneous triangularizability means that this algebra is conjugate into the Lie subalgebra of upper triangular matrices, and is equivalent to this algebra being a Lie subalgebra of a Borel subalgebra.
The basic result is that the (over an algebraically closed field), commuting matrices 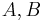 or more generally
or more generally  are simultaneously triangularizable. This can be proven by first showing that commuting matrices have a common eigenvector, and then inducting on dimension as before. This was proven by Frobenius, starting in 1878 for a commuting pair, as discussed at commuting matrices. As for a single matrix, over the complex numbers these can be triangularized by unitary matrices.
are simultaneously triangularizable. This can be proven by first showing that commuting matrices have a common eigenvector, and then inducting on dimension as before. This was proven by Frobenius, starting in 1878 for a commuting pair, as discussed at commuting matrices. As for a single matrix, over the complex numbers these can be triangularized by unitary matrices.
The fact that commuting matrices have a common eigenvector can be interpreted as a result of Hilbert's Nullstellensatz: commuting matrices form a commutative algebra ![K[A_1,\ldots,A_k]](/2012-wikipedia_en_all_nopic_01_2012/I/dbda72e2b1b61f51a1442bd1781ff5de.png) over
over ![K[x_1,\ldots,x_k]](/2012-wikipedia_en_all_nopic_01_2012/I/779553a2b74d2a329828422ea3b2993a.png) which can be interpreted as a variety in k-dimensional affine space, and the existence of a (common) eigenvalue (and hence a common eigenvector) corresponds to this variety having a point (being non-empty), which is the content of the (weak) Nullstellensatz. In algebraic terms, these operators correspond to an algebra representation of the polynomial algebra in k variables.
which can be interpreted as a variety in k-dimensional affine space, and the existence of a (common) eigenvalue (and hence a common eigenvector) corresponds to this variety having a point (being non-empty), which is the content of the (weak) Nullstellensatz. In algebraic terms, these operators correspond to an algebra representation of the polynomial algebra in k variables.
This is generalized by Lie's theorem, which shows that any representation of a solvable Lie algebra is simultaneously upper triangularisable, the case of commuting matrices being the abelian Lie algebra case, abelian being a fortiori solvable.
More generally and precisely, a set of matrices  is simultaneously triangularisable if and only if the matrix
is simultaneously triangularisable if and only if the matrix ![p(A_1,\ldots,A_k)[A_i,A_j]](/2012-wikipedia_en_all_nopic_01_2012/I/38c2cea024e76c24642eb10a47f57c88.png) is nilpotent for all polynomials p in k non-commuting variables, where
is nilpotent for all polynomials p in k non-commuting variables, where ![[A_i,A_j]](/2012-wikipedia_en_all_nopic_01_2012/I/80daa455b55366bd4046000ae0ef741f.png) is the commutator; note that for commuting
is the commutator; note that for commuting 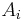 the commutator vanishes so this holds. This was proven in (Drazin, Dungey & Gruenberg 1951); a brief proof is given in (Prasolov 1994, pp. 178–179). One direction is clear: if the matrices are simultaneously triangularisable, then
the commutator vanishes so this holds. This was proven in (Drazin, Dungey & Gruenberg 1951); a brief proof is given in (Prasolov 1994, pp. 178–179). One direction is clear: if the matrices are simultaneously triangularisable, then ![[A_i, A_j]](/2012-wikipedia_en_all_nopic_01_2012/I/80daa455b55366bd4046000ae0ef741f.png) is strictly upper triangularizable (hence nilpotent), which is preserved by multiplication by any
is strictly upper triangularizable (hence nilpotent), which is preserved by multiplication by any 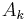 or combination thereof – it will still have 0s on the diagonal in the triangularizing basis.
or combination thereof – it will still have 0s on the diagonal in the triangularizing basis.
Generalizations
Because the product of two upper triangular matrices is again upper triangular, the set of upper triangular matrices forms an algebra. Algebras of upper triangular matrices have a natural generalization in functional analysis which yields nest algebras on Hilbert spaces.
A non-square (or sometimes any) matrix with zeros above (below) the diagonal is called a lower (upper) trapezoidal matrix. The non-zero entries form the shape of a trapezoid.
Borel subgroups and Borel subalgebras
The set of invertible triangular matrices of a given kind (upper or lower) forms a group, indeed a Lie group, which is a subgroup of the general linear group of all invertible matrices; invertible is equivalent to all diagonal entries being invertible (non-zero).
Over the real numbers, this group is disconnected, having 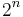 components accordingly as each diagonal entry is positive or negative. The identity component is invertible triangular matrices with positive entries on the diagonal, and the group of all invertible triangular matrices is a semidirect product of this group and diagonal entries with
components accordingly as each diagonal entry is positive or negative. The identity component is invertible triangular matrices with positive entries on the diagonal, and the group of all invertible triangular matrices is a semidirect product of this group and diagonal entries with 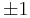 on the diagonal, corresponding to the components.
on the diagonal, corresponding to the components.
The Lie algebra of the Lie group of invertible upper triangular matrices is the set of all upper triangular matrices, not necessarily invertible, and is a solvable Lie algebra. These are, respectively, the standard Borel subgroup B of the Lie group GLn and the standard Borel subalgebra 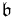 of the Lie algebra gln.
of the Lie algebra gln.
The upper triangular matrices are precisely those that stabilize the standard flag. The invertible ones among them form a subgroup of the general linear group, whose conjugate subgroups are those defined as the stabilizer of some (other) complete flag. These subgroups are Borel subgroups. The group of invertible lower triangular matrices is such a subgroup, since it is the stabilizer of the standard flag associated to the standard basis in reverse order.
The stabilizer of a partial flag obtained by forgetting some parts of the standard flag can be described as a set of block upper triangular matrices (but its elements are not all triangular matrices). The conjugates of such a group are the subgroups defined as the stabilizer of some partial flag. These subgroups are called parabolic subgroups.
Examples
The group of 2 by 2 upper unitriangular matrices is isomorphic to the additive group of the field of scalars; in the case of complex numbers it corresponds to a group formed of parabolic Möbius transformations; the 3 by 3 upper unitriangular matrices form the Heisenberg group.
Examples
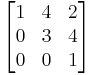
The matrix
is upper triangular and
is lower triangular.
The matrix
is atomic lower triangular. Its inverse is
Forward and back substitution
A matrix equation in the form 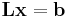 or
or 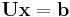 is very easy to solve by an iterative process called forward substitution for lower triangular matrices and analogously back substitution for upper triangular matrices. The process is so called because for lower triangular matrices, one first computes
is very easy to solve by an iterative process called forward substitution for lower triangular matrices and analogously back substitution for upper triangular matrices. The process is so called because for lower triangular matrices, one first computes 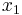 , then substitutes that forward into the next equation to solve for
, then substitutes that forward into the next equation to solve for 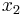 , and repeats through to
, and repeats through to 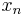 . In an upper triangular matrix, one works backwards, first computing
. In an upper triangular matrix, one works backwards, first computing 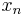 , then substituting that back into the previous equation to solve for
, then substituting that back into the previous equation to solve for 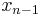 , and repeating through
, and repeating through 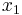 .
.
Notice that this does not require inverting the matrix.
Forward substitution
The matrix equation Lx = b can be written as a system of linear equations
Observe that the first equation (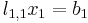 ) only involves
) only involves 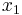 , and thus one can solve for
, and thus one can solve for 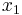 directly. The second equation only involves
directly. The second equation only involves 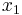 and
and 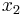 , and thus can be solved once one substitutes in the already solved value for
, and thus can be solved once one substitutes in the already solved value for 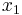 . Continuing in this way, the
. Continuing in this way, the  -th equation only involves
-th equation only involves 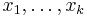 , and one can solve for
, and one can solve for 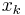 using the previously solved values for
using the previously solved values for 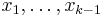 .
.
The resulting formulas are:
A matrix equation with an upper triangular matrix U can be solved in an analogous way, only working backwards.
Algorithm
The following is an example implementation of this algorithm in the C# programming language. Note that the algorithm performs poorly in C# due to the inefficient handling of non-jagged matrices in this language. Nonetheless, the method of forward and backward substitution can be highly efficient.
double[] luEvaluate(double[,] L, double[,] U, Vector b) { // Ax = b -> LUx = b. Then y is defined to be Ux int i = 0; int j = 0; int n = b.Count; double[] x = new double[n]; double[] y = new double[n]; // Forward solve Ly = b for (i = 0; i < n; i++) { y[i] = b[i]; for (j = 0; j < i; j++) { y[i] -= L[i, j] * y[j]; } y[i] /= L[i, i]; } // Backward solve Ux = y for (i = n - 1; i >= 0; i--) { x[i] = y[i]; for (j = i + 1; j < n; j++) { x[i] -= U[i, j] * x[j]; } x[i] /= U[i, i]; } return x; }
Applications
Forward substitution is used in financial bootstrapping to construct a yield curve.
See also
- Linear algebra
- Gaussian elimination
- QR decomposition
- Cholesky decomposition
- Hessenberg matrix
- Tridiagonal matrix
- Invariant subspace
Notes
References
- ^ a b c (Axler 1996, pp. 86–87, 169)
- ^ (Herstein 1975, pp. 285–290)
- Axler, Sheldon (1996), Linear Algebra Done Right, Springer-Verlag, ISBN 0-387-98258-2
- Drazin, M. P.; Dungey, J. W.; Gruenberg, K. W. (1951), "Some theorems on commutative matrices", J. London Math. Soc. 26: 221–228, http://jlms.oxfordjournals.org/cgi/pdf_extract/s1-26/3/221
- Herstein, I. N. (1975), Topics in Algebra (2nd edition ed.), John Wiley and Sons, ISBN 0-471-01090-1
- Prasolov, Viktor (1994), Problems and theorems in linear algebra, http://books.google.com/books?id=fuONq1od6nsC&lpg=PP1&dq=victor%20prasolov%20Problems%20and%20theorems%20in%20linear%20algebra&pg=PP1#v=onepage&q&f=false
|
||||||||||||||