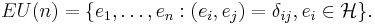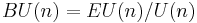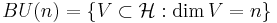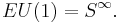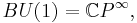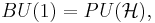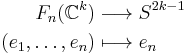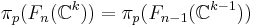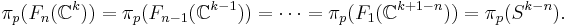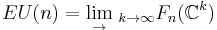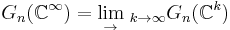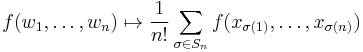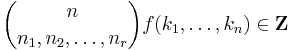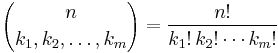Classifying space for U(n)
In mathematics, the classifying space for the unitary group U(n) is a space B(U(n)) together with a universal bundle E(U(n)) such that any hermitian bundle on a paracompact space X is the pull-back of E by a map X → B unique up to homotopy.
This space with its universal fibration may be constructed as either
- the Grassmannian of n-planes in an infinite-dimensional complex Hilbert space; or,
- the direct limit, with the induced topology, of Grassmannians of n planes.
Both constructions are detailed here.
Contents |
Construction as an infinite Grassmannian
The total space 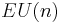 of the universal bundle is given by
of the universal bundle is given by
Here, H is an infinite-dimensional complex Hilbert space, the 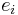 are vectors in H, and
are vectors in H, and 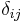 is the Kronecker delta. The symbol
is the Kronecker delta. The symbol 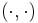 is the inner product on H. Thus, we have that EU(n) is the space of orthonormal n-frames in H.
is the inner product on H. Thus, we have that EU(n) is the space of orthonormal n-frames in H.
The group action of U(n) on this space is the natural one. The base space is then
and is the set of Grassmannian n-dimensional subspaces (or n-planes) in H. That is,
so that V is an n-dimensional vector space.
Case of line bundles
In the case of 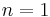 , one has
, one has
known to be a contractible space.
The base space is then
the infinite-dimensional complex projective space. Thus, the set of isomorphism classes of circle bundles over a manifold  are in one-to-one correspondence with the homotopy classes of maps from
are in one-to-one correspondence with the homotopy classes of maps from  to
to 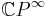 .
.
One also has the relation that
that is, 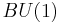 is the infinite-dimensional projective unitary group. See that article for additional discussion and properties.
is the infinite-dimensional projective unitary group. See that article for additional discussion and properties.
For a torus T, which is abstractly isomorphic to  , but need not have a chosen identification, one writes
, but need not have a chosen identification, one writes 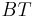 .
.
The topological K-theory 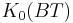 is given by numerical polynomials; more details below.
is given by numerical polynomials; more details below.
Construction as an inductive limit
Let 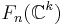 be the space of orthonormal families of
be the space of orthonormal families of  vectors in
vectors in 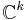 and let
and let 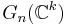 be the Grassmannian of
be the Grassmannian of  -dimensional subvector spaces of
-dimensional subvector spaces of 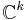 . The total space of the universal bundle can be taken to be the direct limit of the
. The total space of the universal bundle can be taken to be the direct limit of the 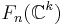 as
as  goes to infinity, while the base space is the direct limit of the
goes to infinity, while the base space is the direct limit of the 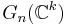 as
as  goes to infinity.
goes to infinity.
Validity of the construction
In this section, we will define the topology on EU(n) and prove that EU(n) is indeed contractible.
Let 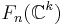 be the space of orthonormal families of
be the space of orthonormal families of  vectors in
vectors in 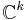 . The group
. The group 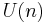 acts freely on
acts freely on 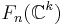 and the quotient is the Grassmannian
and the quotient is the Grassmannian 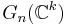 of
of  -dimensional subvector spaces of
-dimensional subvector spaces of 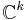 . The map
. The map
is a fibre bundle of fibre 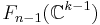 . Thus because
. Thus because 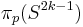 is trivial and because of the long exact sequence of the fibration, we have
is trivial and because of the long exact sequence of the fibration, we have
whenever 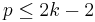 . By taking
. By taking  big enough, precisely for
big enough, precisely for 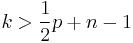 , we can repeat the process and get
, we can repeat the process and get
This last group is trivial for k > n + p. Let
be the direct limit of all the 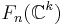 (with the induced topology). Let
(with the induced topology). Let
be the direct limit of all the 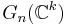 (with the induced topology).
(with the induced topology).
Lemma
The group 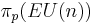 is trivial for all
is trivial for all 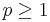 .
.
Proof Let  be a map from the sphere
be a map from the sphere 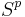 to EU(n). As
to EU(n). As 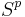 is compact, there exists
is compact, there exists  such that
such that 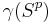 is included in
is included in 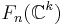 . By taking
. By taking  big enough, we see that
big enough, we see that  is homotopic, with respect to the base point, to the constant map.
is homotopic, with respect to the base point, to the constant map. 
In addition, 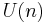 acts freely on
acts freely on 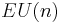 . The spaces
. The spaces 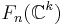 and
and 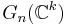 are CW-complexes. One can find a decomposition of these spaces into CW-complexes such that the decomposition of
are CW-complexes. One can find a decomposition of these spaces into CW-complexes such that the decomposition of 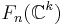 , resp.
, resp. 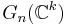 , is induced by restriction of the one for
, is induced by restriction of the one for 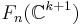 , resp.
, resp. 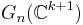 . Thus
. Thus 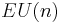 (and also
(and also 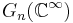 ) is a CW-complex. By Whitehead Theorem and the above Lemma,
) is a CW-complex. By Whitehead Theorem and the above Lemma, 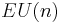 is contractible.
is contractible.
Cohomology of 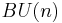
Proposition
The cohomology of the classifying space 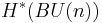 is a ring of polynomials in
is a ring of polynomials in  variables
variables  where
where 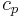 is of degree
is of degree 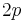 .
.
Proof Let us first consider the case 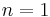 . In this case,
. In this case, 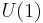 is the circle
is the circle 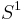 and the universal bundle is
and the universal bundle is 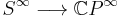 . It is well known[1] that the cohomology of
. It is well known[1] that the cohomology of 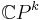 is isomorphic to
is isomorphic to 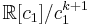 , where
, where 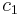 is the Euler class of the
is the Euler class of the 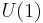 -bundle
-bundle  , and that the injections
, and that the injections 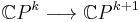 , for
, for 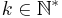 , are compatible with these presentations of the cohomology of the projective spaces. This proves the Proposition for
, are compatible with these presentations of the cohomology of the projective spaces. This proves the Proposition for 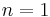 .
.
In the general case, let  be the subgroup of diagonal matrices. It is a maximal torus in
be the subgroup of diagonal matrices. It is a maximal torus in 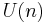 . Its classifying space is
. Its classifying space is 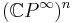 and its cohomology is
and its cohomology is  , where
, where  is the Euler class of the tautological bundle over the i-th
is the Euler class of the tautological bundle over the i-th 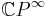 . The Weyl group acts on
. The Weyl group acts on  by permuting the diagonal entries, hence it acts on
by permuting the diagonal entries, hence it acts on 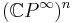 by permutation of the factors. The induced action on its cohomology is the permutation of the
by permutation of the factors. The induced action on its cohomology is the permutation of the  's. We deduce
's. We deduce
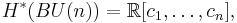
where the 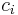 's are the symmetric polynomials in the
's are the symmetric polynomials in the  's.
's. 
K-theory of 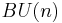
The topological K-theory is known explicitly in terms of numerical symmetric polynomials.
The K-theory reduces to computing 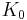 , since K-theory is 2-periodic by the Bott periodicity theorem, and
, since K-theory is 2-periodic by the Bott periodicity theorem, and 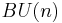 is a limit of complex manifolds, so it has a CW-structure with only cells in even dimensions, so odd K-theory vanishes.
is a limit of complex manifolds, so it has a CW-structure with only cells in even dimensions, so odd K-theory vanishes.
Thus 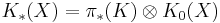 , where
, where ![\pi_*(K)=\mathbf{Z}[t,t^{-1}]](/2012-wikipedia_en_all_nopic_01_2012/I/d95cfecf099455db72e6c3f50a72785f.png) , where t is the Bott generator.
, where t is the Bott generator.
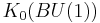 is the ring of numerical polynomials in w, regarded as a subring of
is the ring of numerical polynomials in w, regarded as a subring of ![H_*(BU(1);\mathbf{Q})=\mathbf{Q}[w]](/2012-wikipedia_en_all_nopic_01_2012/I/1f8c38db29d2bffad3fd6f287d42087b.png) , where w is element dual to tautological bundle.
, where w is element dual to tautological bundle.
For the n-torus, 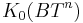 is numerical polynomials in n variables. The map
is numerical polynomials in n variables. The map 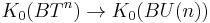 is onto, via a splitting principle, as
is onto, via a splitting principle, as 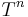 is the maximal torus of
is the maximal torus of 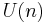 . The map is the symmetrization map
. The map is the symmetrization map
and the image can be identified as the symmetric polynomials satisfying the integrality condition that
where
is the multinomial coefficient and  contains r distinct integers, repeated
contains r distinct integers, repeated 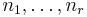 times, respectively.
times, respectively.
See also
Notes
- ^ R. Bott, L. W. Tu -- Differential Forms in Algebraic Topology, Graduate Texts in Mathematics 82, Springer
References
- S. Ochanine, L. Schwartz (1985), "Une remarque sur les générateurs du cobordisme complex", Math. Z. 190 (4): 543–557, doi:10.1007/BF01214753 Contains a description of
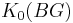 as a
as a 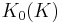 -comodule for any compact, connected Lie group.
-comodule for any compact, connected Lie group. - L. Schwartz (1983), "K-théorie et homotopie stable", Thesis (Université de Paris–VII) Explicit description of
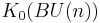
- A. Baker, F. Clarke, N. Ray, L. Schwartz (1989), "On the Kummer congruences and the stable homotopy of BU", Trans. Amer. Math. Soc. (American Mathematical Society) 316 (2): 385–432, doi:10.2307/2001355, JSTOR 2001355