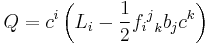BRST quantization
In theoretical physics, BRST quantization (where the BRST refers to Becchi, Rouet, Stora and Tyutin) is a relatively rigorous mathematical approach to quantizing a field theory with a gauge symmetry. Quantization rules in earlier QFT frameworks resembled "prescriptions" or "heuristics" more than proofs, especially in non-abelian QFT, where the use of "ghost fields" with superficially bizarre properties is almost unavoidable for technical reasons related to renormalization and anomaly cancellation. The BRST supersymmetry was introduced in the mid-1970s and was quickly understood to justify the introduction of these Faddeev–Popov ghosts and their exclusion from "physical" asymptotic states when performing QFT calculations. Work by other authors a few years later related the BRST operator to the existence of a rigorous alternative to path integrals when quantizing a gauge theory.
Only in the late 1980s, when QFT was reformulated in fiber bundle language for application to problems in the topology of low-dimensional manifolds, did it become apparent that the BRST "transformation" is fundamentally geometrical in character. In this light, "BRST quantization" becomes more than an alternate way to arrive at anomaly-cancelling ghosts. It is a different perspective on what the ghost fields represent, why the Faddeev–Popov method works, and how it is related to the use of Hamiltonian mechanics to construct a perturbative framework. The relationship between gauge invariance and "BRST invariance" forces the choice of a Hamiltonian system whose states are composed of "particles" according to the rules familiar from the canonical quantization formalism. This esoteric consistency condition therefore comes quite close to explaining how quanta and fermions arise in physics to begin with.
Contents |
Technical summary
BRST quantization (or the BRST formalism) is a differential geometric approach to performing consistent, anomaly-free perturbative calculations in a non-abelian gauge theory. The analytical form of the BRST "transformation" and its relevance to renormalization and anomaly cancellation were described by Carlo Maria Becchi, Alain Rouet, and Raymond Stora in a series of papers culminating in the 1976 "Renormalization of gauge theories". The equivalent transformation and many of its properties were independently discovered by Igor Viktorovich Tyutin. Its significance for rigorous canonical quantization of a Yang–Mills theory and its correct application to the Fock space of instantaneous field configurations were elucidated by Kugo Taichiro and Ojima Izumi. Later work by many authors, notably Thomas Schücker and Edward Witten, has clarified the geometric significance of the BRST operator and related fields and emphasized its importance to topological quantum field theory and string theory.
In the BRST approach, one selects a perturbation-friendly gauge fixing procedure for the action principle of a gauge theory using the differential geometry of the gauge bundle on which the field theory lives. One then quantizes the theory to obtain a Hamiltonian system in the interaction picture in such a way that the "unphysical" fields introduced by the gauge fixing procedure resolve gauge anomalies without appearing in the asymptotic states of the theory. The result is a set of Feynman rules for use in a Dyson series perturbative expansion of the S-matrix which guarantee that it is unitary and renormalizable at each loop order—in short, a coherent approximation technique for making physical predictions about the results of scattering experiments.
Classical BRST
This is related to a supersymplectic manifold where pure operators are graded by integral ghost numbers and we have a BRST cohomology.
Gauge transformations in QFT
From a practical perspective, a quantum field theory consists of an action principle and a set of procedures for performing perturbative calculations. There are other kinds of "sanity checks" that can be performed on a quantum field theory to determine whether it fits qualitative phenomena such as quark confinement and asymptotic freedom. However, most of the predictive successes of quantum field theory, from quantum electrodynamics to the present day, have been quantified by matching S-matrix calculations against the results of scattering experiments.
In the early days of QFT, one would have to have said that the quantization and renormalization prescriptions were as much part of the model as the Lagrangian density, especially when they relied on the powerful but mathematically ill-defined path integral formalism. It quickly became clear that QED was almost "magical" in its relative tractability, and that most of the ways that one might imagine extending it would not produce rational calculations. However, one class of field theories remained promising: gauge theories, in which the objects in the theory represent equivalence classes of physically indistinguishable field configurations, any two of which are related by a gauge transformation. This generalizes the QED idea of a local change of phase to a more complicated Lie group.
QED itself is a gauge theory, as is general relativity, although the latter has proven resistant to quantization so far, for reasons related to renormalization. Another class of gauge theories with a non-Abelian gauge group, beginning with Yang–Mills theory, became amenable to quantization in the late 1960s and early 1970s, largely due to the work of Ludwig D. Faddeev, Victor Popov, Bryce DeWitt, and Gerardus 't Hooft. However, they remained very difficult to work with until the introduction of the BRST method. The BRST method provided the calculation techniques and renormalizability proofs needed to extract accurate results from both "unbroken" Yang–Mills theories and those in which the Higgs mechanism leads to spontaneous symmetry breaking. Representatives of these two types of Yang–Mills systems—quantum chromodynamics and electroweak theory—appear in the Standard Model of particle physics.
It has proven rather more difficult to prove the existence of non-Abelian quantum field theory in a rigorous sense than to obtain accurate predictions using semi-heuristic calculation schemes. This is because analyzing a quantum field theory requires two mathematically interlocked perspectives: a Lagrangian system based on the action functional, composed of fields with distinct values at each point in spacetime and local operators which act on them, and a Hamiltonian system in the Dirac picture, composed of states which characterize the entire system at a given time and field operators which act on them. What makes this so difficult in a gauge theory is that the objects of the theory are not really local fields on spacetime; they are right-invariant local fields on the principal gauge bundle, and different local sections through a portion of the gauge bundle, related by passive transformations, produce different Dirac pictures.
What is more, a description of the system as a whole in terms of a set of fields contains many redundant degrees of freedom; the distinct configurations of the theory are equivalence classes of field configurations, so that two descriptions which are related to one another by an active gauge transformation are also really the same physical configuration. The "solutions" of a quantized gauge theory exist not in a straightforward space of fields with values at every point in spacetime but in a quotient space (or cohomology) whose elements are equivalence classes of field configurations. Hiding in the BRST formalism is a system for parameterizing the variations associated with all possible active gauge transformations and correctly accounting for their physical irrelevance during the conversion of a Lagrangian system to a Hamiltonian system.
Gauge fixing and perturbation theory
The principle of gauge invariance is essential to constructing a workable quantum field theory. But it is generally not feasible to perform a perturbative calculation in a gauge theory without first "fixing the gauge"—adding terms to the Lagrangian density of the action principle which "break the gauge symmetry" to suppress these "unphysical" degrees of freedom. The idea of gauge fixing goes back to the Lorenz gauge approach to electromagnetism, which suppresses most of the excess degrees of freedom in the four-potential while retaining manifest Lorentz invariance. The Lorenz gauge is a great simplification relative to Maxwell's field-strength approach to classical electrodynamics, and illustrates why it is useful to deal with excess degrees of freedom in the representation of the objects in a theory at the Lagrangian stage, before passing over to Hamiltonian mechanics via the Legendre transform.
The Hamiltonian density is related to the Lie derivative of the Lagrangian density with respect to a unit timelike horizontal vector field on the gauge bundle. In a quantum mechanical context it is conventionally rescaled by a factor 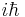 . Integrating it by parts over a spacelike cross section recovers the form of the integrand familiar from canonical quantization. Because the definition of the Hamiltonian involves a unit time vector field on the base space, a horizontal lift to the bundle space, and a spacelike surface "normal" (in the Minkowski metric) to the unit time vector field at each point on the base manifold, it is dependent both on the connexion and the choice of Lorentz frame, and is far from being globally defined. But it is an essential ingredient in the perturbative framework of quantum field theory, into which the quantized Hamiltonian enters via the Dyson series.
. Integrating it by parts over a spacelike cross section recovers the form of the integrand familiar from canonical quantization. Because the definition of the Hamiltonian involves a unit time vector field on the base space, a horizontal lift to the bundle space, and a spacelike surface "normal" (in the Minkowski metric) to the unit time vector field at each point on the base manifold, it is dependent both on the connexion and the choice of Lorentz frame, and is far from being globally defined. But it is an essential ingredient in the perturbative framework of quantum field theory, into which the quantized Hamiltonian enters via the Dyson series.
For perturbative purposes, we gather the configuration of all the fields of our theory on an entire three-dimensional horizontal spacelike cross section of  into one object (a Fock state), and then describe the "evolution" of this state over time using the interaction picture. The Fock space is spanned by the multi-particle eigenstates of the "unperturbed" or "non-interaction" portion
into one object (a Fock state), and then describe the "evolution" of this state over time using the interaction picture. The Fock space is spanned by the multi-particle eigenstates of the "unperturbed" or "non-interaction" portion  of the Hamiltonian
of the Hamiltonian 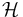 . Hence the instantaneous description of any Fock state is a complex-amplitude-weighted sum of eigenstates of
. Hence the instantaneous description of any Fock state is a complex-amplitude-weighted sum of eigenstates of  . In the interaction picture, we relate Fock states at different times by prescribing that each eigenstate of the unperturbed Hamiltonian experiences a constant rate of phase rotation proportional to its energy (the corresponding eigenvalue of the unperturbed Hamiltonian).
. In the interaction picture, we relate Fock states at different times by prescribing that each eigenstate of the unperturbed Hamiltonian experiences a constant rate of phase rotation proportional to its energy (the corresponding eigenvalue of the unperturbed Hamiltonian).
Hence, in the zero-order approximation, the set of weights characterizing a Fock state does not change over time, but the corresponding field configuration does. In higher approximations, the weights also change; collider experiments in high-energy physics amount to measurements of the rate of change in these weights (or rather integrals of them over distributions representing uncertainty in the initial and final conditions of a scattering event). The Dyson series captures the effect of the discrepancy between  and the true Hamiltonian
and the true Hamiltonian 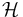 , in the form of a power series in the coupling constant
, in the form of a power series in the coupling constant  ; it is the principal tool for making quantitative predictions from a quantum field theory.
; it is the principal tool for making quantitative predictions from a quantum field theory.
To use the Dyson series to calculate anything, one needs more than a gauge-invariant Lagrangian density; one also needs the quantization and gauge fixing prescriptions that enter into the Feynman rules of the theory. The Dyson series produces infinite integrals of various kinds when applied to the Hamiltonian of a particular QFT. This is partly because all usable quantum field theories to date must be considered effective field theories, describing only interactions on a certain range of energy scales that we can experimentally probe and therefore vulnerable to ultraviolet divergences. These are tolerable as long as they can be handled via standard techniques of renormalization; they are not so tolerable when they result in an infinite series of infinite renormalizations or, worse, in an obviously unphysical prediction such as an uncancelled gauge anomaly. There is a deep relationship between renormalizability and gauge invariance, which is easily lost in the course of attempts to obtain tractable Feynman rules by fixing the gauge.
Pre-BRST approaches to gauge fixing
The traditional gauge fixing prescriptions of continuum electrodynamics select a unique representative from each gauge-transformation-related equivalence class using a constraint equation such as the Lorenz gauge 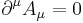 . This sort of prescription can be applied to an Abelian gauge theory such as QED, although it results in some difficulty in explaining why the Ward identities of the classical theory carry over to the quantum theory—in other words, why Feynman diagrams containing internal longitudinally polarized virtual photons do not contribute to S-matrix calculations. This approach also does not generalize well to non-Abelian gauge groups such as the SU(2) of Yang–Mills and electroweak theory and the SU(3) of quantum chromodynamics. It suffers from Gribov ambiguities and from the difficulty of defining a gauge fixing constraint that is in some sense "orthogonal" to physically significant changes in the field configuration.
. This sort of prescription can be applied to an Abelian gauge theory such as QED, although it results in some difficulty in explaining why the Ward identities of the classical theory carry over to the quantum theory—in other words, why Feynman diagrams containing internal longitudinally polarized virtual photons do not contribute to S-matrix calculations. This approach also does not generalize well to non-Abelian gauge groups such as the SU(2) of Yang–Mills and electroweak theory and the SU(3) of quantum chromodynamics. It suffers from Gribov ambiguities and from the difficulty of defining a gauge fixing constraint that is in some sense "orthogonal" to physically significant changes in the field configuration.
More sophisticated approaches do not attempt to apply a delta function constraint to the gauge transformation degrees of freedom. Instead of "fixing" the gauge to a particular "constraint surface" in configuration space, one can break the gauge freedom with an additional, non-gauge-invariant term added to the Lagrangian density. In order to reproduce the successes of gauge fixing, this term is chosen to be minimal for the choice of gauge that corresponds to the desired constraint and to depend quadratically on the deviation of the gauge from the constraint surface. By the stationary phase approximation on which the Feynman path integral is based, the dominant contribution to perturbative calculations will come from field configurations in the neighborhood of the constraint surface.
The perturbative expansion associated with this Lagrangian, using the method of functional quantization, is generally referred to as the  gauge. It reduces in the case of an Abelian U(1) gauge to the same set of Feynman rules that one obtains in the method of canonical quantization. But there is an important difference: the broken gauge freedom appears in the functional integral as an additional factor in the overall normalization. This factor can only be pulled out of the perturbative expansion (and ignored) when the contribution to the Lagrangian of a perturbation along the gauge degrees of freedom is independent of the particular "physical" field configuration. This is the condition that fails to hold for non-Abelian gauge groups. If one ignores the problem and attempts to use the Feynman rules obtained from "naive" functional quantization, one finds that one's calculations contain unremovable anomalies.
gauge. It reduces in the case of an Abelian U(1) gauge to the same set of Feynman rules that one obtains in the method of canonical quantization. But there is an important difference: the broken gauge freedom appears in the functional integral as an additional factor in the overall normalization. This factor can only be pulled out of the perturbative expansion (and ignored) when the contribution to the Lagrangian of a perturbation along the gauge degrees of freedom is independent of the particular "physical" field configuration. This is the condition that fails to hold for non-Abelian gauge groups. If one ignores the problem and attempts to use the Feynman rules obtained from "naive" functional quantization, one finds that one's calculations contain unremovable anomalies.
The problem of perturbative calculations in QCD was solved by introducing additional fields known as Faddeev–Popov ghosts, whose contribution to the gauge-fixed Lagrangian offsets the anomaly introduced by the coupling of "physical" and "unphysical" perturbations of the non-Abelian gauge field. From the functional quantization perspective, the "unphysical" perturbations of the field configuration (the gauge transformations) form a subspace of the space of all (infinitesimal) perturbations; in the non-Abelian case, the embedding of this subspace in the larger space depends on the configuration around which the perturbation takes place. The ghost term in the Lagrangian represents the functional determinant of the Jacobian of this embedding, and the properties of the ghost field are dictated by the exponent desired on the determinant in order to correct the functional measure on the remaining "physical" perturbation axes.
Mathematical approach to BRST
BRST construction,[1][2] applies to a situation of a hamiltonian action of a compact, connected Lie group  on a phase space
on a phase space  . Let
. Let  be the Lie algebra of
be the Lie algebra of  and
and 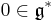 a regular value of the moment map
a regular value of the moment map 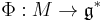 . Let
. Let  . Assume the
. Assume the  -action on
-action on 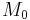 is free and proper, and consider the space
is free and proper, and consider the space  of
of  -orbits on
-orbits on 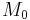 , which is also known as a Symplectic Reduction quotient
, which is also known as a Symplectic Reduction quotient  .
.
First, using the regular sequence of functions defining 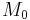 inside
inside  , construct a Koszul complex
, construct a Koszul complex  . The differential,
. The differential, 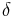 , on this complex is an odd
, on this complex is an odd 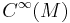 -linear derivation of the graded
-linear derivation of the graded 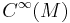 -algebra
-algebra  . This odd derivation is defined by extending the Lie algebra homomorphim
. This odd derivation is defined by extending the Lie algebra homomorphim  of the hamiltonian action. The resulting Koszul complex is the Koszul complex of the
of the hamiltonian action. The resulting Koszul complex is the Koszul complex of the  -module
-module 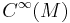 , where
, where  is the symmetric algebra of
is the symmetric algebra of  , and the module structure comes from a ring homomorphism
, and the module structure comes from a ring homomorphism 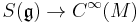 induced by the hamiltonian action
induced by the hamiltonian action  .
.
This Koszul complex is a resolution of the  -module
-module  , i.e.,
, i.e.,
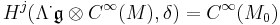 , if
, if 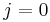 and zero otherwise.
and zero otherwise.
Then, consider the Chevalley-Eilenberg cochain complex for the Koszul complex  considered as a dg module over the Lie algebra
considered as a dg module over the Lie algebra 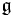 :
:
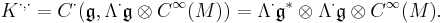
The "horizontal" differential 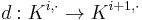 is defined on the coefficients
is defined on the coefficients  by the action of
by the action of  and on
and on  as the exterior derivative of right-invariant differential forms on the Lie group
as the exterior derivative of right-invariant differential forms on the Lie group  , whose Lie algebra is
, whose Lie algebra is  .
.
Let  be a complex such that
be a complex such that 
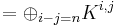 with a differential
with a differential  . The cohomology groups of
. The cohomology groups of  are computed using a spectral sequence associated to the double complex
are computed using a spectral sequence associated to the double complex  .
.
The first term of the spectral sequence computes the cohomology of the "vertical" differential  :
:
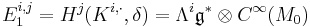 , if
, if 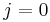 and zero otherwise.
and zero otherwise.
The first term of the spectral sequence may be interpreted as the complex of vertical differential forms  for the fiber bundle
for the fiber bundle  .
.
The second term of the spectral sequence computes the cohomology of the "horizontal" differential  on
on 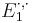 :
:
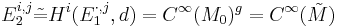 , if
, if 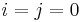 and zero otherwise.
and zero otherwise.
The spectral sequence collapses at the second term, so that  , which is concentrated in degree zero.
, which is concentrated in degree zero.
Therefore,  , if p = 0 and 0 otherwise.
, if p = 0 and 0 otherwise.
The BRST operator and asymptotic Fock space
Two important remarks about the BRST operator are due. First, instead of working with the gauge group  one can use only the action of the gauge algebra
one can use only the action of the gauge algebra  on the fields (functions on the phase space).
on the fields (functions on the phase space).
Second, the variation of any "BRST exact form" 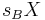 with respect to a local gauge transformation
with respect to a local gauge transformation  is
is ![[i_{\delta\lambda},\, s_B] s_B X = i_{\delta\lambda} (s_B s_B X) %2B s_B (i_{\delta\lambda} (s_B X)) = s_B (i_{\delta\lambda} (s_B X))](/2012-wikipedia_en_all_nopic_01_2012/I/9dffe2129c14ef5f555930a768c7551b.png) , which is itself an exact form.
, which is itself an exact form.
More importantly for the Hamiltonian perturbative formalism (which is carried out not on the fiber bundle but on a local section), adding a BRST exact term to a gauge invariant Lagrangian density preserves the relation  . As we shall see, this implies that there is a related operator
. As we shall see, this implies that there is a related operator 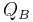 on the state space for which
on the state space for which ![[Q_B,\, \mathcal{H}] = 0](/2012-wikipedia_en_all_nopic_01_2012/I/96a398066b10f7282e048cfb80beb2b5.png) —i. e., the BRST operator on Fock states is a conserved charge of the Hamiltonian system. This implies that the time evolution operator in a Dyson series calculation will not evolve a field configuration obeying
—i. e., the BRST operator on Fock states is a conserved charge of the Hamiltonian system. This implies that the time evolution operator in a Dyson series calculation will not evolve a field configuration obeying 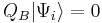 into a later configuration with
into a later configuration with 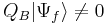 (or vice versa).
(or vice versa).
Another way of looking at the nilpotence of the BRST operator is to say that its image (the space of BRST exact forms) lies entirely within its kernel (the space of BRST closed forms). (The "true" Lagrangian, presumed to be invariant under local gauge transformations, is in the kernel of the BRST operator but not in its image.) The preceding argument says that we can limit our universe of initial and final conditions to asymptotic "states"—field configurations at timelike infinity, where the interaction Lagrangian is "turned off"—that lie in the kernel of 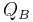 and still obtain a unitary scattering matrix. (BRST closed and exact states are defined similarly to BRST closed and exact fields; closed states are annihilated by
and still obtain a unitary scattering matrix. (BRST closed and exact states are defined similarly to BRST closed and exact fields; closed states are annihilated by 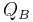 , while exact states are those obtainable by applying
, while exact states are those obtainable by applying 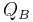 to some arbitrary field configuration.)
to some arbitrary field configuration.)
We can also suppress states that lie inside the image of 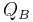 when defining the asymptotic states of our theory—but the reasoning is a bit subtler. Since we have postulated that the "true" Lagrangian of our theory is gauge invariant, the true "states" of our Hamiltonian system are equivalence classes under local gauge transformation; in other words, two initial or final states in the Hamiltonian picture that differ only by a BRST exact state are physically equivalent. However, the use of a BRST exact gauge breaking prescription does not guarantee that the interaction Hamiltonian will preserve any particular subspace of closed field configurations that we can call "orthogonal" to the space of exact configurations. (This is a crucial point, often mishandled in QFT textbooks. There is no a priori inner product on field configurations built into the action principle; we construct such an inner product as part of our Hamiltonian perturbative apparatus.)
when defining the asymptotic states of our theory—but the reasoning is a bit subtler. Since we have postulated that the "true" Lagrangian of our theory is gauge invariant, the true "states" of our Hamiltonian system are equivalence classes under local gauge transformation; in other words, two initial or final states in the Hamiltonian picture that differ only by a BRST exact state are physically equivalent. However, the use of a BRST exact gauge breaking prescription does not guarantee that the interaction Hamiltonian will preserve any particular subspace of closed field configurations that we can call "orthogonal" to the space of exact configurations. (This is a crucial point, often mishandled in QFT textbooks. There is no a priori inner product on field configurations built into the action principle; we construct such an inner product as part of our Hamiltonian perturbative apparatus.)
We therefore focus on the vector space of BRST closed configurations at a particular time with the intention of converting it into a Fock space of intermediate states suitable for Hamiltonian perturbation. To this end, we shall endow it with ladder operators for the energy-momentum eigenconfigurations (particles) of each field, complete with appropriate (anti-)commutation rules, as well as a positive semi-definite inner product. We require that the inner product be singular exclusively along directions that correspond to BRST exact eigenstates of the unperturbed Hamiltonian. This ensures that one can freely choose, from within the two equivalence classes of asymptotic field configurations corresponding to particular initial and final eigenstates of the (unbroken) free-field Hamiltonian, any pair of BRST closed Fock states that we like.
The desired quantization prescriptions will also provide a quotient Fock space isomorphic to the BRST cohomology, in which each BRST closed equivalence class of intermediate states (differing only by an exact state) is represented by exactly one state that contains no quanta of the BRST exact fields. This is the Fock space we want for asymptotic states of the theory; even though we will not generally succeed in choosing the particular final field configuration to which the gauge-fixed Lagrangian dynamics would have evolved that initial configuration, the singularity of the inner product along BRST exact degrees of freedom ensures that we will get the right entries for the physical scattering matrix.
(Actually, we should probably be constructing a Krein space for the BRST-closed intermediate Fock states, with the time reversal operator playing the role of the "fundamental symmetry" relating the Lorentz-invariant and positive semi-definite inner products. The asymptotic state space is presumably the Hilbert space obtained by quotienting BRST exact states out of this Krein space.)
In sum, no field introduced as part of a BRST gauge fixing procedure will appear in asymptotic states of the gauge-fixed theory. However, this does not imply that we can do without these "unphysical" fields in the intermediate states of a perturbative calculation! This is because perturbative calculations are done in the interaction picture. They implicitly involve initial and final states of the non-interaction Hamiltonian  , gradually transformed into states of the full Hamiltonian in accordance with the adiabatic theorem by "turning on" the interaction Hamiltonian (the gauge coupling). The expansion of the Dyson series in terms of Feynman diagrams will include vertices that couple "physical" particles (those that can appear in asymptotic states of the free Hamiltonian) to "unphysical" particles (states of fields that live outside the kernel of
, gradually transformed into states of the full Hamiltonian in accordance with the adiabatic theorem by "turning on" the interaction Hamiltonian (the gauge coupling). The expansion of the Dyson series in terms of Feynman diagrams will include vertices that couple "physical" particles (those that can appear in asymptotic states of the free Hamiltonian) to "unphysical" particles (states of fields that live outside the kernel of 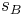 or inside the image of
or inside the image of 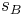 ) and vertices that couple "unphysical" particles to one another.
) and vertices that couple "unphysical" particles to one another.
The Kugo–Ojima answer to unitarity questions
T. Kugo and I. Ojima are commonly credited with the discovery of the principal QCD color confinement criterion. Their role in obtaining a correct version of the BRST formalism in the Lagrangian framework seems to be less widely appreciated. It is enlightening to inspect their variant of the BRST transformation, which emphasizes the hermitian properties of the newly introduced fields, before proceeding from an entirely geometrical angle. The gauge fixed Lagrangian density is below; the two terms in parentheses form the coupling between the gauge and ghost sectors, and the final term becomes a Gaussian weighting for the functional measure on the auxiliary field  .
.
The Faddeev–Popov ghost field  is unique among the new fields of our gauge-fixed theory in having a geometrical meaning beyond the formal requirements of the BRST procedure. It is a version of the Maurer–Cartan form on
is unique among the new fields of our gauge-fixed theory in having a geometrical meaning beyond the formal requirements of the BRST procedure. It is a version of the Maurer–Cartan form on 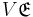 , which relates each right-invariant vertical vector field
, which relates each right-invariant vertical vector field 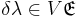 to its representation (up to a phase) as a
to its representation (up to a phase) as a  -valued field. This field must enter into the formulas for infinitesimal gauge transformations on objects (such as fermions
-valued field. This field must enter into the formulas for infinitesimal gauge transformations on objects (such as fermions  , gauge bosons
, gauge bosons 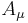 , and the ghost
, and the ghost  itself) which carry a non-trivial representation of the gauge group. The BRST transformation with respect to
itself) which carry a non-trivial representation of the gauge group. The BRST transformation with respect to 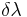 is therefore:
is therefore:
Here we have omitted the details of the matter sector  and left the form of the Ward operator on it unspecified; these are unimportant so long as the representation of the gauge algebra on the matter fields is consistent with their coupling to
and left the form of the Ward operator on it unspecified; these are unimportant so long as the representation of the gauge algebra on the matter fields is consistent with their coupling to  . The properties of the other fields we have added are fundamentally analytical rather than geometric. The bias we have introduced towards connections with
. The properties of the other fields we have added are fundamentally analytical rather than geometric. The bias we have introduced towards connections with 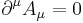 is gauge-dependent and has no particular geometrical significance. The anti-ghost
is gauge-dependent and has no particular geometrical significance. The anti-ghost  is nothing but a Lagrange multiplier for the gauge fixing term, and the properties of the scalar field
is nothing but a Lagrange multiplier for the gauge fixing term, and the properties of the scalar field  are entirely dictated by the relationship
are entirely dictated by the relationship  . (The new fields are all Hermitian in Kugo–Ojima conventions, but the parameter
. (The new fields are all Hermitian in Kugo–Ojima conventions, but the parameter 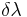 is an anti-Hermitian "anti-commuting
is an anti-Hermitian "anti-commuting  -number". This results in some unnecessary awkwardness with regard to phases and passing infinitesimal parameters through operators; this will be resolved with a change of conventions in the geometric treatment below.)
-number". This results in some unnecessary awkwardness with regard to phases and passing infinitesimal parameters through operators; this will be resolved with a change of conventions in the geometric treatment below.)
We already know, from the relation of the BRST operator to the exterior derivative and the Faddeev–Popov ghost to the Maurer–Cartan form, that the ghost  corresponds (up to a phase) to a
corresponds (up to a phase) to a  -valued 1-form on
-valued 1-form on 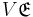 . In order for integration of a term like
. In order for integration of a term like  to be meaningful, the anti-ghost
to be meaningful, the anti-ghost  must carry representations of these two Lie algebras—the vertical ideal
must carry representations of these two Lie algebras—the vertical ideal 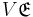 and the gauge algebra
and the gauge algebra  —dual to those carried by the ghost. In geometric terms,
—dual to those carried by the ghost. In geometric terms,  must be fiberwise dual to
must be fiberwise dual to  and one rank short of being a top form on
and one rank short of being a top form on 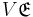 . Likewise, the auxiliary field
. Likewise, the auxiliary field  must carry the same representation of
must carry the same representation of  (up to a phase) as
(up to a phase) as  , as well as the representation of
, as well as the representation of 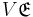 dual to its trivial representation on
dual to its trivial representation on 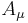 —i. e., B is a fiberwise
—i. e., B is a fiberwise  -dual top form on
-dual top form on 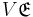 .
.
Let us focus briefly on the one-particle states of the theory, in the adiabatically decoupled limit  . There are two kinds of quanta in the Fock space of the gauge-fixed Hamiltonian that we expect to lie entirely outside the kernel of the BRST operator: those of the Faddeev–Popov anti-ghost
. There are two kinds of quanta in the Fock space of the gauge-fixed Hamiltonian that we expect to lie entirely outside the kernel of the BRST operator: those of the Faddeev–Popov anti-ghost  and the forward polarized gauge boson. (This is because no combination of fields containing
and the forward polarized gauge boson. (This is because no combination of fields containing  is annihilated by
is annihilated by 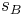 and we have added to the Lagrangian a gauge breaking term that is equal up to a divergence to
and we have added to the Lagrangian a gauge breaking term that is equal up to a divergence to  .) Likewise, there are two kinds of quanta that will lie entirely in the image of the BRST operator: those of the Faddeev–Popov ghost
.) Likewise, there are two kinds of quanta that will lie entirely in the image of the BRST operator: those of the Faddeev–Popov ghost  and the scalar field
and the scalar field  , which is "eaten" by completing the square in the functional integral to become the backward polarized gauge boson. These are the four types of "unphysical" quanta which will not appear in the asymptotic states of a perturbative calculation—if we get our quantization rules right.
, which is "eaten" by completing the square in the functional integral to become the backward polarized gauge boson. These are the four types of "unphysical" quanta which will not appear in the asymptotic states of a perturbative calculation—if we get our quantization rules right.
The anti-ghost is taken to be a Lorentz scalar for the sake of Poincaré invariance in  . However, its (anti-)commutation law relative to
. However, its (anti-)commutation law relative to  —i. e., its quantization prescription, which ignores the spin-statistics theorem by giving Fermi–Dirac statistics to a spin-0 particle—will be given by the requirement that the inner product on our Fock space of asymptotic states be singular along directions corresponding to the raising and lowering operators of some combination of non-BRST-closed and BRST-exact fields. This last statement is the key to "BRST quantization", as opposed to mere "BRST symmetry" or "BRST transformation".
—i. e., its quantization prescription, which ignores the spin-statistics theorem by giving Fermi–Dirac statistics to a spin-0 particle—will be given by the requirement that the inner product on our Fock space of asymptotic states be singular along directions corresponding to the raising and lowering operators of some combination of non-BRST-closed and BRST-exact fields. This last statement is the key to "BRST quantization", as opposed to mere "BRST symmetry" or "BRST transformation".
- (Needs to be completed in the language of BRST cohomology, with reference to the Kugo–Ojima treatment of asymptotic Fock space.)
Gauge bundles and the vertical ideal
In order to do the BRST method justice, we must switch from the "algebra-valued fields on Minkowski space" picture typical of quantum field theory texts (and of the above exposition) to the language of fiber bundles, in which there are two quite different ways to look at a gauge transformation: as a change of local section (also known in general relativity as a passive transformation) or as the pullback of the field configuration along a vertical diffeomorphism of the principal bundle. It is the latter sort of gauge transformation that enters into the BRST method. Unlike a passive transformation, it is well-defined globally on a principal bundle with any structure group over an arbitrary manifold; this is important in several approaches to a Theory of Everything. (However, for concreteness and relevance to conventional QFT, this article will stick to the case of a principal gauge bundle with compact fiber over 4-dimensional Minkowski space.)
A principal gauge bundle  over a 4-manifold
over a 4-manifold  is locally isomorphic to
is locally isomorphic to  , where the fiber
, where the fiber  is isomorphic to a Lie group
is isomorphic to a Lie group  , the gauge group of the field theory. (This is an isomorphism of manifold structures, not of group structures; there is no special surface in
, the gauge group of the field theory. (This is an isomorphism of manifold structures, not of group structures; there is no special surface in  corresponding to
corresponding to 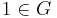 , so it is more proper to say that the fiber
, so it is more proper to say that the fiber  is a
is a  -torsor.) Its most basic property as a fiber bundle is the "projection to the base space"
-torsor.) Its most basic property as a fiber bundle is the "projection to the base space"  , which defines the "vertical" directions on
, which defines the "vertical" directions on  (those lying within the fiber
(those lying within the fiber 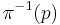 over each point
over each point 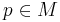 ). As a gauge bundle it has a left action of
). As a gauge bundle it has a left action of  on
on  which respects the fiber structure, and as a principal bundle it also has a right action of
which respects the fiber structure, and as a principal bundle it also has a right action of  on
on  which also respects the fiber structure and commutes with the left action.
which also respects the fiber structure and commutes with the left action.
The left action of the structure group  on
on  corresponds to a mere change of coordinate system on an individual fiber. The (global) right action
corresponds to a mere change of coordinate system on an individual fiber. The (global) right action 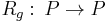 of a (fixed)
of a (fixed) 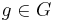 corresponds to an actual automorphism of each fiber and hence to a map of
corresponds to an actual automorphism of each fiber and hence to a map of  to itself. In order for
to itself. In order for  to qualify as a principal
to qualify as a principal  -bundle, the global right action of each
-bundle, the global right action of each 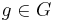 must be an automorphism with respect to the manifold structure of
must be an automorphism with respect to the manifold structure of  with a smooth dependence on
with a smooth dependence on  —i. e., a diffeomorphism from
—i. e., a diffeomorphism from  to
to  .
.
The existence of the global right action of the structure group picks out a special class of right invariant geometric objects on  —those which do not change when they are pulled back along
—those which do not change when they are pulled back along  for all values of
for all values of 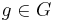 . The most important right invariant objects on a principal bundle are the right invariant vector fields, which form an ideal
. The most important right invariant objects on a principal bundle are the right invariant vector fields, which form an ideal 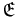 of the Lie algebra of infinitesimal diffeomorphisms on
of the Lie algebra of infinitesimal diffeomorphisms on  . Those vector fields on
. Those vector fields on  which are both right invariant and vertical form an ideal
which are both right invariant and vertical form an ideal 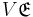 of
of 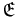 , which has a relationship to the entire bundle
, which has a relationship to the entire bundle  analogous to that of the Lie algebra
analogous to that of the Lie algebra  of the gauge group
of the gauge group  to the individual
to the individual  -torsor fiber
-torsor fiber  .
.
We suppose that the "field theory" of interest is defined in terms of a set of "fields" (smooth maps into various vector spaces) defined on a principal gauge bundle  . Different fields carry different representations of the gauge group
. Different fields carry different representations of the gauge group  , and perhaps of other symmetry groups of the manifold such as the Poincaré group. One may define the space
, and perhaps of other symmetry groups of the manifold such as the Poincaré group. One may define the space  of local polynomials in these fields and their derivatives. The fundamental Lagrangian density of one's theory is presumed to lie in the subspace
of local polynomials in these fields and their derivatives. The fundamental Lagrangian density of one's theory is presumed to lie in the subspace  of polynomials which are real-valued and invariant under any unbroken non-gauge symmetry groups. It is also presumed to be invariant not only under the left action (passive coordinate transformations) and the global right action of the gauge group but also under local gauge transformations—pullback along the infinitesimal diffeomorphism associated with an arbitrary choice of right invariant vertical vector field
of polynomials which are real-valued and invariant under any unbroken non-gauge symmetry groups. It is also presumed to be invariant not only under the left action (passive coordinate transformations) and the global right action of the gauge group but also under local gauge transformations—pullback along the infinitesimal diffeomorphism associated with an arbitrary choice of right invariant vertical vector field  .
.
Identifying local gauge transformations with a particular subspace of vector fields on the manifold  equips us with a better framework for dealing with infinite-dimensional infinitesimals: differential geometry and the exterior calculus. The change in a scalar field under pullback along an infinitesimal automorphism is captured in the Lie derivative, and the notion of retaining only the term linear in the scale of the vector field is implemented by separating it into the inner derivative and the exterior derivative. (In this context, "forms" and the exterior calculus refer exclusively to degrees of freedom which are dual to vector fields on the gauge bundle, not to degrees of freedom expressed in (Greek) tensor indices on the base manifold or (Roman) matrix indices on the gauge algebra.)
equips us with a better framework for dealing with infinite-dimensional infinitesimals: differential geometry and the exterior calculus. The change in a scalar field under pullback along an infinitesimal automorphism is captured in the Lie derivative, and the notion of retaining only the term linear in the scale of the vector field is implemented by separating it into the inner derivative and the exterior derivative. (In this context, "forms" and the exterior calculus refer exclusively to degrees of freedom which are dual to vector fields on the gauge bundle, not to degrees of freedom expressed in (Greek) tensor indices on the base manifold or (Roman) matrix indices on the gauge algebra.)
The Lie derivative on a manifold is a globally well-defined operation in a way that the partial derivative is not. The proper generalization of Clairaut's theorem to the non-trivial manifold structure of  is given by the Lie bracket of vector fields and the nilpotence of the exterior derivative. And we obtain an essential tool for computation: the generalized Stokes theorem, which allows us to integrate by parts and drop the surface term as long as the integrand drops off rapidly enough in directions where there is an open boundary. (This is not a trivial assumption, but can be dealt with by renormalization techniques such as dimensional regularization as long as the surface term can be made gauge invariant.)
is given by the Lie bracket of vector fields and the nilpotence of the exterior derivative. And we obtain an essential tool for computation: the generalized Stokes theorem, which allows us to integrate by parts and drop the surface term as long as the integrand drops off rapidly enough in directions where there is an open boundary. (This is not a trivial assumption, but can be dealt with by renormalization techniques such as dimensional regularization as long as the surface term can be made gauge invariant.)
BRST formalism
In theoretical physics, the BRST formalism is a method of implementing first class constraints. The letters BRST stand for Becchi, Rouet, Stora, and (independently) Tyutin who discovered this formalism. It is a sophisticated method to deal with quantum physical theories with gauge invariance. For example, the BRST methods are often applied to gauge theory and quantized general relativity.
Quantum version
The space of states is not a Hilbert space (see below). This vector space is both Z2-graded and R-graded. If you wish, you may think of it as a Z2×R-graded vector space. The former grading is the parity, which can either be even or odd. The latter grading is the ghost number. Note that it is R and not Z because unlike the classical case, we can have nonintegral ghost numbers. Operators acting upon this space are also Z2×R-graded in the obvious manner. In particular, Q is odd and has a ghost number of 1.
Let Hn be the subspace of all states with ghost number n. Then, Q restricted to Hn maps Hn to Hn+1. Since Q²=0, we have a cochain complex describing a cohomology.
The physical states are identified as elements of cohomology of the operator  , i.e. as vectors in Ker Qn+1/Im Qn. The BRST theory is in fact linked to the standard resolution in Lie algebra cohomology.
, i.e. as vectors in Ker Qn+1/Im Qn. The BRST theory is in fact linked to the standard resolution in Lie algebra cohomology.
Recall that the space of states is Z2-graded. If A is a pure graded operator, then the BRST transformation maps A to [Q,A) where [,) is the supercommutator. BRST-invariant operators are operators for which [Q,A)=0. Since the operators are also graded by ghost numbers, this BRST transformation also forms a cohomology for the operators since [Q,[Q,A))=0.
Although the BRST formalism is more general than the Faddeev-Popov gauge fixing, in the special case where it is derived from it, the BRST operator is also useful to obtain the right Jacobian associated with constraints that gauge-fix the symmetry.
The BRST is a supersymmetry. It generates the Lie superalgebra with a zero-dimensional even part and a one dimensional odd part spanned by Q. [Q,Q)={Q,Q}=0 where [,) is the Lie superbracket (i.e. Q²=0). This means Q acts as an antiderivation.
Because Q is Hermitian and its square is zero but Q itself is nonzero, this means the vector space of all states prior to the cohomological reduction has an indefinite norm! This means it is not a Hilbert space.
For more general flows which can't be described by first class constraints, see Batalin–Vilkovisky_formalism.
Example
For the special case of gauge theories (of the usual kind described by sections of a principal G-bundle) with a quantum connection form A, a BRST charge (sometimes also a BRS charge) is an operator usually denoted  .
.
Let the  -valued gauge fixing conditions be
-valued gauge fixing conditions be  where ξ is a positive number determining the gauge. There are many other possible gauge fixings, but they will not be covered here. The fields are the
where ξ is a positive number determining the gauge. There are many other possible gauge fixings, but they will not be covered here. The fields are the  -valued connection form A,
-valued connection form A,  -valued scalar field with fermionic statistics, b and c and a
-valued scalar field with fermionic statistics, b and c and a  -valued scalar field with bosonic statistics B. c deals with the gauge transformations wheareas b and B deal with the gauge fixings. There actually are some subtleties associated with the gauge fixing due to Gribov ambiguities but they will not be covered here.
-valued scalar field with bosonic statistics B. c deals with the gauge transformations wheareas b and B deal with the gauge fixings. There actually are some subtleties associated with the gauge fixing due to Gribov ambiguities but they will not be covered here.
where D is the covariant derivative.
where [,]L is the Lie bracket, NOT the commutator.
Q is an antiderivation.
The BRST Lagrangian density
While the Lagrangian density isn't BRST invariant, its integral over all of spacetime, the action is.
The operator  is defined as
is defined as
where 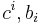 are the Faddeev–Popov ghosts and antighosts (fields with a negative ghost number), respectively,
are the Faddeev–Popov ghosts and antighosts (fields with a negative ghost number), respectively,  are the infinitesimal generators of the Lie group, and
are the infinitesimal generators of the Lie group, and  are its structure constants.
are its structure constants.
See also
References
Textbook treatments
- Chapter 16 of Peskin & Schroeder (ISBN 0-201-50397-2 or ISBN 0-201-50934-2) applies the "BRST symmetry" to reason about anomaly cancellation in the Faddeev–Popov Lagrangian. This is a good start for QFT non-experts, although the connections to geometry are omitted and the treatment of asymptotic Fock space is only a sketch.
- Chapter 12 of M. Göckeler and T. Schücker. (ISBN 0-521-37821-4 or ISBN 0-521-32960-4) discusses the relationship between the BRST formalism and the geometry of gauge bundles. It is substantially similar to Schücker's 1987 paper
Primary literature
Original BRST papers:
- C. Becchi, A. Rouet and R. Stora, Phys. Lett. B52 (1974) 344.
- C. Becchi, A. Rouet and R. Stora, Commun. Math. Phys. 42 (1975) 127.
- C. Becchi, A. Rouet and R. Stora, "Renormalization of gauge theories", Ann. Phys. 98, 2 (1976) pp. 287–321.
- I.V. Tyutin, "Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism", Lebedev Physics Institute preprint 39 (1975), arXiv:0812.0580.
- The commonly cited Kugo–Ojima paper: T. Kugo and I. Ojima, "Local Covariant Operator Formalism of Non-Abelian Gauge Theories and Quark Confinement Problem", Suppl. Progr. Theor. Phys. 66 (1979) p. 14
- A more accessible version of Kugo–Ojima is available online in a series of papers, starting with: T. Kugo, I. Ojima, "Manifestly Covariant Canonical Formulation of the Yang–Mills Field Theories. I", Progr. Theor. Phys. 60, 6 (1978) pp. 1869–1889. This is probably the single best reference for BRST quantization in quantum mechanical (as opposed to geometrical) language.
- Much insight about the relationship between topological invariants and the BRST operator may be found in: E. Witten, "Topological quantum field theory", Commun. Math. Phys. 117, 3 (1988), pp. 353–386
Alternate perspectives
- BRST systems are briefly analyzed from an operator theory perspective in: S. S. Horuzhy and A. V. Voronin, "Remarks on Mathematical Structure of BRST Theories", Comm. Math. Phys. 123, 4 (1989) pp. 677–685
- A measure-theoretic perspective on the BRST method may be found in Carlo Becchi's 1996 lecture notes.



![\delta c = - \delta\lambda \frac{g}{2} [c,\,c]](/2012-wikipedia_en_all_nopic_01_2012/I/da2d8fb0aa65dbf12cb5c36f92fc0f52.png)


![Qc={i\over 2}[c,c]_L](/2012-wikipedia_en_all_nopic_01_2012/I/fcec4bf21969fc72424e1c0b97e326af.png)

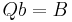
![\mathcal{L}=-{1\over 4g^2} \operatorname{Tr}[F^{\mu\nu}F_{\mu\nu}]%2B{1\over 2g^2} \operatorname{Tr}[BB]-{1\over g^2} \operatorname{Tr}[BG]-{\xi\over g^2} \operatorname{Tr}[\partial^\mu b D_\mu c]](/2012-wikipedia_en_all_nopic_01_2012/I/2507aa70d165e58a39d4b4ba5e668e06.png)