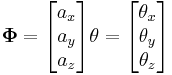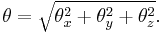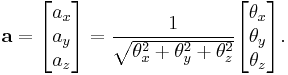Axis-angle representation
The axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis (straight line), and an angle describing the magnitude of the rotation about the axis. The rotation occurs in the sense prescribed by the right-hand rule.
This representation evolves from Euler's rotation theorem, which implies that any rotation or sequence of rotations of a rigid body in a three-dimensional space is equivalent to a pure rotation about a single fixed axis.
The axis-angle representation is equivalent to the more concise rotation vector, or Euler vector representation. In this case, both the axis and the angle are represented by a non-normalized vector codirectional with the axis whose magnitude is the rotation angle.
Rodrigues' rotation formula can be used to apply to a vector a rotation represented by an axis and an angle.
Contents |
Uses
The axis-angle representation is convenient when dealing with rigid body dynamics. It is useful to both characterize rotations, and also for converting between different representations of rigid body motion, such as homogeneous transformations and twists.
Example
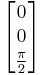
Say you are standing on the ground and you pick the direction of gravity to be the negative z direction. Then if you turn to your left, you will travel 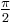 radians (or 90 degrees) about the z axis. In axis-angle representation, this would be
radians (or 90 degrees) about the z axis. In axis-angle representation, this would be
This can be represented as a rotation vector with a magnitude of 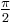 pointing in the z direction.
pointing in the z direction.
Rotating a vector
Rodrigues' rotation formula (named after Olinde Rodrigues) is an efficient algorithm for rotating a vector in space, given a rotation axis and an angle of rotation. In other words, the Rodrigues formula provides an algorithm to compute the exponential map from so(3) to SO(3) without computing the full matrix exponent (the rotation matrix).
If v is a vector in 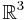 and ω is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed sense), the Rodrigues formula to obtain the rotated vector is:
and ω is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed sense), the Rodrigues formula to obtain the rotated vector is:
This is more efficient than converting ω and θ into a rotation matrix, and using the rotation matrix to compute the rotated vector.
Relationship to other representations
There are many ways to represent a rotation. It is useful to understand how different representations relate to one another, and how to convert between them.
Exponential map from so(3) to SO(3)
The exponential map is used as a transformation from axis-angle representation of rotations to rotation matrices.
Essentially, by using a Taylor expansion you can derive a closed form relationship between these two representations. Given an axis, 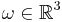 having length 1, and an angle,
having length 1, and an angle, 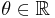 , an equivalent rotation matrix is given by the following:
, an equivalent rotation matrix is given by the following:
where R is a 3x3 rotation matrix and the hat operator gives the antisymmetric matrix equivalent of the cross product. This can be easily derived from Rodrigues' rotation formula.
Log map from SO(3) to so(3)
To retrieve the axis-angle representation of a rotation matrix calculate the angle of rotation:
and then use it to find the normalized axis:
Note, also that the Matrix logarithm of the rotation matrix R is:
Except when R has eigenvalues equal to -1 where the log is not unique. However, even in the case where 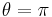 the Frobenius norm of the log is:
the Frobenius norm of the log is:
Note that given rotation matrices A and B:
is the geodesic distance on the 3D manifold of rotation matrices.
Unit Quaternions
To transform from axis-angle coordinates to unit quaternions use the following expression:
Given a unit quaternion, the axis-angle coordinates can be extracted using the following:
It may also be useful to know:
Simultaneous orthogonal rotations angle
Multiplying the rotation axis and angle gives vector SORA:
where 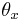 ,
, 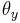 , and
, and 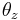 represent angles of three simultaneous rotations around orthogonal axes. It holds:
represent angles of three simultaneous rotations around orthogonal axes. It holds:
and
See also
- SO(3) - the group of all rotations in three dimensional space
- Charts on SO(3) for other representations
- rotation group - a mathematical look at rotations
- homogeneous coordinates
- screw theory - a representation of rigid body motions and velocities using the concepts of twists, screws and wrenches
- Rotation around a fixed axis
- Rotation representation (mathematics)
- Rodrigues' rotation formula
- Simultaneous orthogonal rotations angle
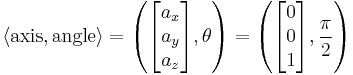
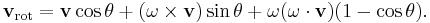
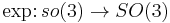
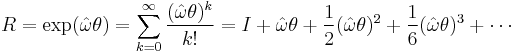
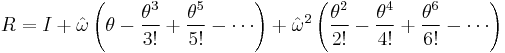
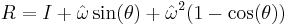
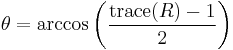
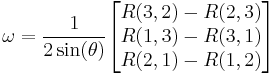
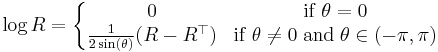
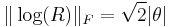
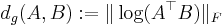
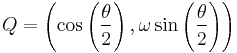
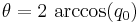
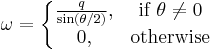
![\frac{q}{ \sin( \theta/2 ) } =
\frac{[q_1 q_2 q_3]^\top}{ \|{[q_1 q_2 q_3]^\top}\|}](/2012-wikipedia_en_all_nopic_01_2012/I/78d97ceb8160cf3cf3083f48b5df99f1.png)