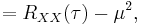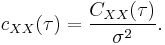Autocovariance
In statistics, given a real stochastic process X(t), the autocovariance is the covariance of the variable with itself, i.e. the variance of the variable against a time-shifted version of itself. If the process has the mean E[Xt] = μt, then the autocovariance is given by
where E is the expectation operator.
Contents |
Stationarity
If X(t) is stationary process, then the following conditions are true:
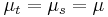 for all t, s
for all t, s
and
where
is the lag time, or the amount of time by which the signal has been shifted.
As a result, the autocovariance becomes
where RXX represents the autocorrelation in the signal processing sense.
Normalization
When normalized by dividing by the variance σ2, the autocovariance C becomes the autocorrelation coefficient function c[1],
The autocovariance function is itself a version of the autocorrelation function with the mean level removed. If the signal has a mean of 0, the autocovariance and autocorrelation functions are identical [1].
However, often the autocovariance is called autocorrelation even if this normalization has not been performed.
The autocovariance can be thought of as a measure of how similar a signal is to a time-shifted version of itself with an autocovariance of σ2 indicating perfect correlation at that lag. The normalisation with the variance will put this into the range [−1, 1].
Properties
The autocovariance of a linearly filtered process 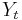
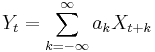
- is
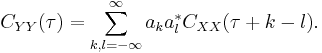
See also
References
- P. G. Hoel, Mathematical Statistics, Wiley, New York, 1984.
![C_{XX}(t,s) = E[(X_t - \mu_t)(X_s - \mu_s)] = E[X_t X_s] - \mu_t \mu_s.\,](/2012-wikipedia_en_all_nopic_01_2012/I/280a7a52105cda9a719e6ce0e0c144da.png)
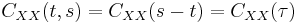
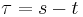
![C_{XX}(\tau) = E[(X(t) - \mu)(X(t%2B\tau) - \mu)]\,](/2012-wikipedia_en_all_nopic_01_2012/I/0a0f0b0322067c9d8ae3f934a2cf0dcb.png)
![= E[X(t) X(t%2B\tau)] - \mu^2\,](/2012-wikipedia_en_all_nopic_01_2012/I/cb52602daac4d4c667f5e678b70076d1.png)