Auction theory

Auction theory is an applied branch of economics which deals with how people act in auction markets and researches the properties of auction markets. There are many possible designs (or sets of rules) for an auction and typical issues studied by auction theorists include the efficiency of a given auction design, optimal and equilibrium bidding strategies, and revenue comparison. Auction theory is also used as a tool to inform the design of real-world auctions; most notably auctions for the privatisation of public-sector companies or the sale of licenses for use of the electromagnetic spectrum.

1 General idea
2 Types of auction
3 Game-theoretic models
4 Revenue equivalence
5 Winner's curse
6 JEL classification
7 Footnotes
8 Further reading
9 External links

General idea

Auctions take many forms but always satisfy two conditions:

(i) They may be used to sell any item and so are universal, also

(ii) The outcome of the auction does not depend on the identity of the bidders; i.e., auctions are anonymous.

Most auctions have the feature that participants submit bids, amounts of money they are willing to pay. Standard auctions require that the winner of the auction is the participant with the highest bid. A nonstandard auction does not require this (e.g. a lottery).

Types of auction

There are traditionally four types of auction that are used for the allocation of a single item:

First-price sealed-bid auctions in which bidders place their bid in a sealed envelope and simultaneously hand them to the auctioneer. The envelopes are opened and the individual with the highest bid wins, paying a price equal to the exact amount that he or she bid.
Second-price sealed-bid auctions (Vickrey auctions) in which bidders place their bid in a sealed envelope and simultaneously hand them to the auctioneer. The envelopes are opened and the individual with the highest bid wins, paying a price equal to the exact amount of the second highest bid.
Open Ascending-bid auctions (English auctions) in which the price is steadily raised by the auctioneer with bidders dropping out once the price becomes too high. This continues until there remains only one bidder who wins the auction at the current price.
Open Descending-bid auctions (Dutch auctions) in which the price starts at a level sufficiently high to deter all bidders and is progressively lowered until a bidder indicates that he is prepared to buy at the current price. He or she wins the auction and pays the price at which they bid.

Most auction theory revolves around these four "standard" auction types. However, other auction types have also received some academic study, such as:

All-pay auctions in which bidders place their bid in a sealed envelope and simultaneously hand them to the auctioneer. The envelopes are opened and the individual with the highest bid wins, paying a price equal to the exact amount that he or she bid. All losing bidders are also required to make a payment to the auctioneer equal to their own bid in an all-pay auction. This auction format is non-standard, but can be used to understand things such as election campaigns (in which bids can be interpreted as campaign spending) or queuing for a scarce commodity (in which your bid is the amount of time for which you are prepared to queue).
Amsterdam auctions, a type of premium auction which begins as an English auction. Once only two bidders remain, each submits a sealed bid. The higher bidder wins, paying either the first or second price. Both finalists receive a premium: a proportion of the excess of the second price over the third price (at which English auction ended)^[1].
Unique bid auctions
Many homogenous item auctions, e.g., spectrum auctions
Simultaneous multiple-round auctions
Position auctions
Generalized second-price auction
Menu auction
Ascending package auction

Game-theoretic models

A game-theoretic auction model is a mathematical game represented by a set of players, a set of actions (strategies) available to each player, and a payoff vector corresponding to each combination of strategies. Generally, the players are the buyer(s) and the seller(s). The action set of each player is a set of bid functions or reservation prices. Each bid function maps the player's value (in the case of a buyer) or cost (in the case of a seller) to a bid price. The payoff of each player under a combination of strategies is the expected utility (or expected profit) of that player under that combination of strategies.

Game-theoretic models of auctions and strategic bidding generally fall into either of the following two categories. In a private value model, each participant (bidder) assumes that each of the competing bidders obtains a random private value from a probability distribution. In a common value model, each participant assumes that any other participant obtains a random signal from a probability distribution common to all bidders. Usually, but not always, a private values model assumes that the values are independent across bidders, whereas a common value model usually assumes that the values are independent up to the common parameters of the probability distribution.

When it is necessary to make explicit assumptions about bidders' value distributions, most of the published research assumes symmetric bidders. This means that the probability distribution from which the bidders obtain their values (or signals) is identical across bidders. In a private values model which assumes independence, symmetry implies that the bidders' values are independently and identically distributed (i.i.d.). An important example (which does not assume independence) is Milgrom and Weber's "general symmetric model" (1982).^[2]^[3] One of the earlier published theoretical research addressing properties of auctions among asymmetric bidders is Keith Waehrer's 1999 article.^[4] Later published research include Susan Athey's 2001 Econometrica article,^[5] as well as Reny and Zamir (2004).^[6]

In a simple first-price auction model with two buyers bidding for an object, each buyer might assume that the rival buyer's private value is drawn from the uniform distribution over the interval [0,1], with the cumulative distribution function 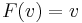$F(v) = v$ . (Since F is symmetric between the two buyers, this is an auction model with symmetric bidders.) Assuming that: (i) the value of the object for the seller is 0, and (ii) the seller's reservation price is also 0,^[7] each buyer's expected utility U as a function of his/her bid price p is equal to the consumer surplus that the buyer will receive conditional on winning 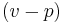$(v - p)$ , multiplied by the likelihood that he or she is going to be the buyer with the highest bid price. That likelihood is given by the probability that this buyer's bid price p exceeds the other buyer's bid price B (expressed as a function of the other buyer's value 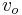$v_o$ ). Express this probability as 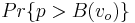$Pr\{p > B(v_o)\}$ . 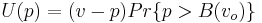Then, $U(p) = (v - p) Pr\{p > B(v_o)\}$ .

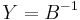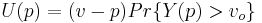Assume that each buyer's equilibrium bid price is monotonically increasing in that buyer's value; this implies that the bid function B has an inverse function. Let Y be the inverse of B: $Y=B^{-1}$ . Then $U(p) = (v - p) Pr\{Y(p) > v_o\}$ .

Since 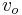$v_o$ is distributed $F(v_o)$ ,

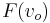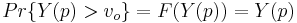
$Pr\{Y(p) > v_o\} = F(Y(p)) = Y(p)$

which implies

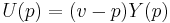$U(p) = (v - p)Y(p)$ .

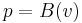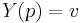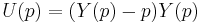Since the buyers are symmetric, in equilibrium it must be the case that $p = B(v)$ or (equivalently) $Y(p) = v$ , so we can rewrite $U(p) = (Y(p) - p)Y(p)$ .

A bid price p maximizes U if U'(p) = 0. Differentiating U with respect to p and setting to zero, 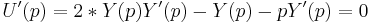$\,U'(p) = 2*Y(p)Y'(p) - Y(p) - pY'(p) = 0$ . A solution 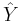$\hat Y$ of this differential equation is an inverse Nash equilibrium strategy of this game.

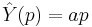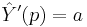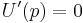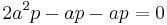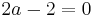At this point, one may conjecture that the (unique) solution is the linear function $\,\hat Y(p) = ap$ and $\,\hat Y'(p) = a$ for some real number a. Substituting into $\,U'(p) = 0$ , $2a^2p - ap - ap = 0$ or $2a - 2 = 0$ , since we assume a≠0 and p≠0. Solving for a yields 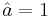$\hat a = 1$ . Therefore 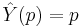$\hat Y(p) = p$ satisfies 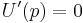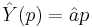$\,U'(p) = 0$ . 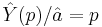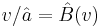$\hat Y(p) = \hat a p$ implies $\hat Y(p)/\hat a = p$ , or $v/\hat a = \hat B(v)$ . Thus, the (unique) Nash equilibrium strategy bidding function of this game is established as 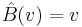$\hat B(v) = v$ , at least within the set of invertible bidding functions. In other words, one should just bid one's private valuation in a private value auction. Lebrun (1996)^[8] provides a more general proof that an equilibrium exists in a first-price auction when the random valuations of the bidders are independent of each other.

Revenue equivalence

One of the major findings of Auction Theory is the celebrated Revenue Equivalence Theorem (first proved by Vickrey in 1961 and generalized 20 years later by Myerson, and independently by Riley and Samuelson.), which states that any allocation mechanism/auction in which (i) the bidder with the highest type/signal/valuation always wins, (ii) the bidder with the lowest possible type/valuation/signal expects zero surplus, (iii) all bidders are risk neutral and (iv) all bidders are drawn from a strictly increasing and atomless distribution will lead to the same expected revenue for the seller (and player i of type v can expect the same surplus across auction types). The winning bid should be epsilon above the second highest valuation. Relaxing these assumptions can provide valuable insights for auction design. Decision biases can also lead to predictable non-equivalencies. Additionally, if some bidders are known to have a higher valuation for the lot, techniques such as price discriminating against such bidders will yield higher returns. (In other words, if a bidder is known to value the lot at $X more than the next highest bidder, the seller can increase their profits by charging that bidder $X-delta more than any other bidder (or equivalently a special bidding fee of $X - delta). This bidder will still win the lot, but will pay more than she would otherwise. ^[9]

Winner's curse

The winner's curse is a phenomenon which can occur in common value settings—when the actual values to the different bidders are unknown but correlated, and the bidders make bidding decisions based on estimated values. In such cases, the winner will tend to be the bidder with the highest estimate, and that winner will frequently have bid too much for the auctioned item.

In an equilibrium of such a game, the winner's curse does not occur because the bidders account for the bias in their bidding strategies. Behaviorally and empirically, however, winner's curse is a common phenomenon. (cf. Richard Thaler).

JEL classification

In the Journal of Economic Literature Classification System C7 is the classification for Game Theory and D44 is the classification for Auctions.^[10]

Footnotes

^ "The Amsterdam Auction". http://129.3.20.41/eps/mic/papers/0205/0205002.pdf. Retrieved 2011-08-27.
^ Milgrom, P., and R. Weber (1982) "A Theory of Auctions and Competitive Bidding," Econometrica Vol. 50 No. 5, pp. 1089–1122.
^ Because bidders in real-world auctions are rarely symmetric, applied scientists began to research auctions with asymmetric value distributions beginning in the late 1980s. Such applied research often depended on numerical solution algorithms to compute an equilibrium and establish its properties. Preston McAfee and John McMillan (1989) simulated bidding for a government contract in which the cost distribution of domestic firms is different from the cost distribution of the foreign firms ("Government Procurement and International Trade," Journal of International Economics, Vol. 26, pp. 291-308.) One of the publications based on the earliest numerical research is Dalkir, S., J. W. Logan, and R. T. Masson, "Mergers in Symmetric and Asymmetric Noncooperative Auction Markets: The Effects on Prices and Efficiency," published in Vol. 18 of The International Journal of Industrial Organization, (2000, pp. 383–413). Other pioneering research include Tschantz, S., P. Crooke, and L. Froeb, "Mergers in Sealed versus Oral Auctions," published in Vol. 7 of The International Journal of the Economics of Business (2000, pp. 201–213).
^ K. Waehrer (1999) "Asymmetric Auctions With Application to Joint Bidding and Mergers," International Journal of Industrial Organization 17: 437-452
^ Athey, S. (2001) "Single Crossing Properties and the Existence of Pure Strategy Equilibria in Games of Incomplete Information," Econometrica Vol. 69 No. 4, pp. 861-890.
^ Reny, P., and S. Zamir (2004) "On the Existence of Pure Strategy Monotone Equilibria in Asymmetric First-Price Auctions," Econometrica, Vol. 72 No. 4, pp. 1105–1125.
^ This assumption implies that the seller is not acting strategically; strictly speaking, the seller is not a player in this example.
^ Lebrun, Bernard (1996) "Existence of an equilibrium in first price auctions," Economic Theory, Vol. 7 No. 3, pp. 421-443.
^ McAfee, , R Preston; & John McMillan. (1987). "Auctions and Bidding". Journal of Economic Literature 25 (2).
^ "Journal of Economic Literature Classification System". American Economic Association. http://aea-web.org/journal/jel_class_system.html. Retrieved 2008-06-25. (D: Microeconomics, D4: Market Structure and Pricing, D44: Auctions)

External links

Auctions on GameTheory.net