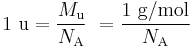Atomic mass
The atomic mass (ma) is the mass of a specific isotope, most often expressed in unified atomic mass units.[1] The atomic mass is the total mass of protons, neutrons and electrons in a single atom.[2]
The atomic mass is sometimes incorrectly used as a synonym of relative atomic mass, average atomic mass and atomic weight; these differ subtly from the atomic mass. The atomic mass is defined as the mass of an atom, which can only be one isotope at a time and is not an abundance-weighted average as in the case of atomic weight. In the case of many elements that have one dominant isotope the actual numerical similarity/difference between the atomic mass of the most common isotope and the relative atomic mass or standard atomic weights can be very small such that it does not affect most bulk calculations—but such an error can be critical when considering individual atoms. For elements with more than one common isotope the difference even to the most common atomic mass can be half a mass unit or more (e.g. chlorine). The atomic mass of an uncommon isotope can differ from the relative atomic mass or standard atomic weight by several mass units.
Standard atomic weight refers to the mean relative atomic mass of an element in the local environment of the Earth's crust and atmosphere as determined by the IUPAC Commission on Atomic Weights and Isotopic Abundances.[3] These are what are included in a standard periodic table and is what is used in most bulk calculations. An uncertainty in brackets is included which often reflects natural variability in isotopic distribution rather than uncertainty in measurement.[4] For synthetic elements the isotope formed depends on the means of synthesis, so the concept of natural isotope abundance has no meaning. Therefore, for synthetic elements the total nucleon count of the most stable isotope (i.e., the isotope with the longest half-life) is listed in brackets in place of the standard atomic weight. Lithium represents a unique case where the natural abundances of the isotopes have been perturbed by human activities to the point of affecting the uncertainty in its standard atomic weight, even in samples obtained from natural sources, such as rivers.
Relative atomic mass is a synonym for atomic weight and closely related to average atomic mass (but not a synonym for atomic mass), the weighted mean of the atomic masses of all the atoms of a chemical element found in a particular sample, weighted by isotopic abundance.[5] This is frequently used as a synonym for the standard atomic weight and it is correct to do so since the standard atomic weights are relative atomic masses, although it is less specific to do so. Relative atomic mass also refers to non-terrestrial environments and highly specific terrestrial environments that deviate from the average or have different certainties (number of significant figures) than the standard atomic weights.
Relative isotopic mass is the relative mass of a given isotope (more specifically, any single nuclide), scaled with carbon-12 as exactly 12. No other nuclides other than carbon-12 have exactly whole-number masses in this scale. This is due to two factors: [1] the different mass of neutrons and protons acting to change the total mass in nuclides with proton/neutron ratios other than the 1:1 ratio of carbon-12; and [2] an exact whole-number will not be located if there exists a loss/gain of mass to difference in mean binding energy relative to the mean binding energy for carbon-12. However, since any mass defect due to binding energy is a small fraction (less than 1%) compared to the mass of a nucleon, and even less compared to the average mass per nucleon in carbon-12, which is moderately strongly bound. Since protons and neutrons differ in mass from each by an even smaller fraction (about 0.0014 u), the practice of rounding the atomic mass of any given nuclide or isotope to the nearest whole number, always gives the simple whole number total nucleon count. Neutron count can then be derived by subtracting the atomic number.
The mass number of a nuclide is simply the total number of nucleons in the nucleus. It is equal to the number of protons (atomic number) plus the number of neutrons. This number is always a simple whole number. It has units of "nucleons" not atomic mass units. An example is oxygen-16, which has 16 nucleons (8 protons and 8 neutrons).
Contents |
Mass defects in atomic masses
The amount that the atomic masses deviate from their mass numbers is as follows: the deviation starts positive at hydrogen-1, becomes negative until a minimum is reached at iron-56, iron-58 and nickel-62, then increases to positive values in the heavy isotopes, with increasing atomic number. This corresponds to the following: nuclear fission in an element heavier than iron produces energy, and fission in any element lighter than iron requires energy. The opposite is true of nuclear fusion reactions: fusion in elements lighter than iron produces energy, and fusion in elements heavier than iron requires energy.
Measurement of atomic masses
Direct comparison and measurement of the masses of atoms is achieved with mass spectrometry.
Conversion factor between atomic mass units and grams
The standard scientific unit for dealing with atoms in macroscopic quantities is the mole (mol), which is defined arbitrarily as the amount of a substance with as many atoms or other units as there are in 12 grams of the carbon isotope C-12. The number of atoms in a mole is called Avogadro's number, the value of which is approximately 6.022 × 1023 mol−1. One mole of a substance always contains almost exactly the relative atomic mass or molar mass of that substance (which is the concept of molar mass), expressed in grams; however, this is almost never true for the atomic mass. For example, the standard atomic weight of iron is 55.847 g/mol, and therefore one mole of iron as commonly found on earth has a mass of 55.847 grams. The atomic mass of an 56Fe isotope is 55.935 u and one mole of 56Fe will in theory weigh 55.935g, but such amounts of pure 56Fe have never been found on Earth.
The formulaic conversion between atomic mass units and SI mass in grams for a single atom is:
where 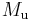 is the Molar mass constant and
is the Molar mass constant and 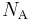 is the Avogadro constant.
is the Avogadro constant.
Relationship between atomic and molecular masses
Similar definitions apply to molecules. One can compute the molecular mass of a compound by adding the atomic masses of its constituent atoms (nuclides). One can compute the molar mass of a compound by adding the relative atomic masses of the elements given in the chemical formula. In both cases the multiplicity of the atoms (the number of times it occurs) must be taken into account, usually by multiplication of each unique mass by its multiplicity.
History
The first scientists to determine atomic weights were John Dalton and Thomas Thomson between 1803 and 1805 and Jöns Jakob Berzelius between 1808 and 1826. Atomic weight was originally defined relative to that of the lightest element hydrogen taken as 1.00, and in the 1820s Prout's hypothesis stated that atomic masses of all elements would prove via a whole number rule to be exact multiples of this hydrogen weight. Berzelius, however, soon proved that this hypothesis did not always hold even approximately, and in some elements, such as chlorine, atomic weight falls almost exactly between two multiples of the hydrogen weight. Still later, as noted, this was shown to be an isotope effect, and that the atomic masses of pure isotopes, or nuclides, are multiples of the hydrogen mass, to within about 1%.
In the 1860s Stanislao Cannizzaro refined atomic weights by applying Avogadro's law (notably at the Karlsruhe Congress of 1860). He formulated a law to determine atomic weights of elements: the different quantities of the same element contained in different molecules are all whole multiples of the atomic weight and determined atomic weights and molecular weights by comparing the vapor density of a collection of gases with molecules containing one or more of the chemical element in question.[6]
In the early twentieth century, up until the 1960s chemists and physicists used two different atomic mass scales. The chemists used a scale such that the natural mixture of oxygen isotopes had an atomic mass 16, while the physicists assigned the same number 16 to the atomic mass of the most common oxygen isotope (containing eight protons and eight neutrons). However, because oxygen-17 and oxygen-18 are also present in natural oxygen this led to 2 different tables of atomic mass. The unified scale based on carbon-12, 12C, met the physicists' need to base the scale on a pure isotope, while being numerically close to the chemists' scale.
The term atomic weight is being phased out slowly and being replaced by relative atomic mass, in most current usage. The history of this shift in nomenclature reaches back to the 1960s and has been the source of much debate in the scientific community. The debate was largely created by the adoption of the unified atomic mass unit and the realization that weight was in some ways an inappropriate term. The argument for keeping the term "atomic weight" was primarily that it was a well understood term to those in the field, that the term "atomic mass" was already in use (as it is currently defined) and that the term "relative atomic mass" was in some ways redundant. In 1979, in a compromise move, the definition was refined and the term "relative atomic mass" was introduced as a secondary synonym. Twenty years later the primacy of these synonyms was reversed and the term "relative atomic mass" is now the preferred term; however the "standard atomic weights" have maintained the same name.[7]
See also
References
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "atomic mass".
- ^ Atomic mass, Encyclopædia Britannica on-line
- ^ IUPAC Definition of Standard Atomic Weight
- ^ ATOMIC WEIGHTS OF THE ELEMENTS 2005 (IUPAC TECHNICAL REPORT), M. E. WIESER Pure Appl. Chem., V.78, pp. 2051, 2006
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "relative atomic mass".
- ^ Williams, Andrew (2007). "Origin of the Formulas of Dihydrogen and Other Simple Molecules". J. Chem. Ed. 84 (11): 1779. doi:10.1021/ed084p1779.
- ^ 'ATOMIC WEIGHT' -THE NAME, ITS HISTORY, DEFINITION, AND UNITS, P. DE BIEVRE and H. S. PEISER Pure&App. Chem., 64, 1535, 1992