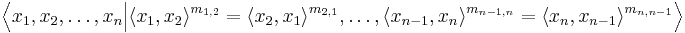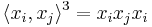Artin group
In mathematics, an Artin group (or generalized braid group) is a group with a presentation of the form
where
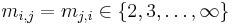 .
.
For 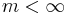 ,
, 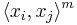 denotes an alternating product of
denotes an alternating product of  and
and 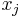 of length
of length  , beginning with
, beginning with  . For example,
. For example,
and
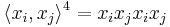 .
.
If 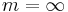 , then there is (by convention) no relation for
, then there is (by convention) no relation for  and
and 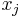 .
.
The integers 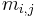 can be organized into a symmetric matrix, known as the Coxeter matrix of the group. Each Artin group has as a quotient the Coxeter group with the same set of generators and Coxeter matrix. The kernel of the homomorphism to the associated Coxeter group, known as the pure Artin group, is generated by relations of the form
can be organized into a symmetric matrix, known as the Coxeter matrix of the group. Each Artin group has as a quotient the Coxeter group with the same set of generators and Coxeter matrix. The kernel of the homomorphism to the associated Coxeter group, known as the pure Artin group, is generated by relations of the form 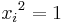 .
.
Contents |
Classes of Artin groups
Braid groups are examples of Artin groups, with Coxeter matrix 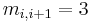 and
and 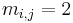 for
for 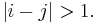 Several important classes of Artin groups can be defined in terms of the properties of the Coxeter matrix.
Several important classes of Artin groups can be defined in terms of the properties of the Coxeter matrix.
Artin groups of finite type
If M is a Coxeter matrix of finite type, so that the corresponding Coxeter group W = A(M) is finite, then the Artin group A = A(M) is called an Artin group of finite type. The 'irreducible types' are labeled as An , Bn = Cn , Dn , I2(n) , F4 , E6 , E7 , E8 , H3 , H4 . A pure Artin group of finite type can be realized as the fundamental group of the complement of a finite hyperplane arrangement in Cn. Pierre Deligne and Brieskorn-Saito have used this geometric description to compute the center of A, its cohomology, and to solve the word and conjugacy problems.
Right-angled Artin groups
If M is a matrix all of whose elements are equal to 2 or ∞, then the corresponding Artin group is called a right-angled Artin group. For this class of Artin groups, a different labeling scheme is commonly used. Any graph Γ on n vertices labeled 1, 2, …, n defines a matrix M, for which mij = 2 if i and j are connected by an edge in Γ, and mij = ∞ otherwise. The right-angled Artin group A(Γ) associated with the matrix M has n generators x1, x2, …, xn and relations
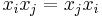 whenever i and j are connected by an edge in
whenever i and j are connected by an edge in 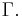
The class of right-angled Artin groups includes the free groups of finite rank, corresponding to a graph with no edges, and the finitely-generated free abelian groups, corresponding to a complete graph. Mladen Bestvina and Noel Brady constructed a nonpositively curved cubical complex K whose fundamental group is a given right-angled Artin group A(Γ). They applied Morse-theoretic arguments to their geometric description of Artin groups and exhibited first known examples of groups with the property (FP2) that are not finitely presented.
References
- Mladen Bestvina, Noel Brady, Morse theory and finiteness properties of groups. Invent. Math. 129 (1997), no. 3, 445-470.
- Pierre Deligne, Les immeubles des groupes de tresses généralisés. Invent. Math. 17 (1972), 273-302.
- Egbert Brieskorn, Kyoji Saito, Artin-Gruppen und Coxeter-Gruppen. Invent. Math. 17 (1972), 245--271.