Armstrong's axioms
Armstrong's axioms are a set of axioms (or, more precisely, inference rules) used to infer all the functional dependencies on a relational database. They were developed by William W. Armstrong on his paper.[1] The axioms are sound in that they generate only functional dependencies in the closure of a set of functional dependencies (denoted as F+) when applied to that set (denoted as F). They are also complete in that repeated application of these rules will generate all functional dependencies in the closure F+.
More formally, let < (
(  ),
),  > denote a relational scheme over the set of attributes
> denote a relational scheme over the set of attributes  with a set of functional dependencies
with a set of functional dependencies  . We say that a functional dependency
. We say that a functional dependency  is logically implied by
is logically implied by  ,and denote it with
,and denote it with 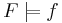 if and only if for every instance
if and only if for every instance  of
of  that satisfies the functional dependencies in
that satisfies the functional dependencies in  , r also satisfies
, r also satisfies  . We denote by
. We denote by 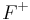 the set of all functional dependencies that are logically implied by F.
the set of all functional dependencies that are logically implied by F.
Furthermore, with respect to a set of inference rules  , we say that a functional dependency
, we say that a functional dependency  is derivable from the functional dependencies in
is derivable from the functional dependencies in  by the set of inference rules
by the set of inference rules  , and we denote it by
, and we denote it by 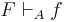 if and only if
if and only if  is obtainable by means of repeatedly applying the inference rules in
is obtainable by means of repeatedly applying the inference rules in  to functional dependencies in
to functional dependencies in  . We denote by
. We denote by 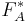 the set of all functional dependencies that are derivable from
the set of all functional dependencies that are derivable from  by inference rules in
by inference rules in  .
.
Then, a set of inference rules  is sound if and only if the following holds:
is sound if and only if the following holds:
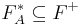
that is to say, we cannot derive by means of  functional dependencies that are not logically implied by
functional dependencies that are not logically implied by  . The set of inference rules
. The set of inference rules  is said to be complete if the following holds:
is said to be complete if the following holds:
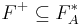
more simply put, we are able to derive by  all the functional dependencies that are logically implied by
all the functional dependencies that are logically implied by  .
.
Contents |
Axioms
Let  (
( ) be a relation scheme over the set of attributes
) be a relation scheme over the set of attributes  . Henceforth we will denote by letters
. Henceforth we will denote by letters  ,
,  ,
,  any subset of
any subset of  and, for short, the union of two sets of attributes
and, for short, the union of two sets of attributes  and
and  by
by  instead of the usual
instead of the usual 
Axiom of reflexivity
If 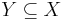 , then
, then 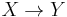
Axiom of augmentation
If 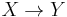 , then
, then 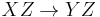 for any
for any 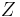
Axiom of transitivity
If 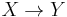 and
and 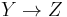 , then
, then 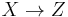
Additional rules
Union
If 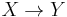 and
and 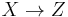 then
then 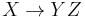
Decomposition
If 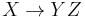 then
then 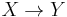 and
and 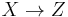
Pseudo Transitivity
If 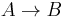 and
and 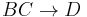 then
then 
External links
References
- ^ William Ward Armstrong: Dependency Structures of Data Base Relationships, page 580-583. IFIP Congress, 1974.
|
||||||||||||||||||||
|
||||||||