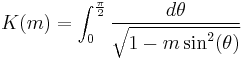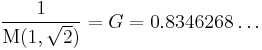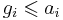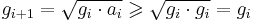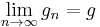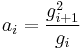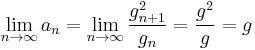Arithmetic-geometric mean
In mathematics, the arithmetic-geometric mean (AGM) of two positive real numbers x and y is defined as follows:
First compute the arithmetic mean of x and y and call it a1. Next compute the geometric mean of x and y and call it g1; this is the square root of the product xy:
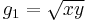 .
.
Then iterate this operation with a1 taking the place of x and g1 taking the place of y. In this way, two sequences (an) and (gn) are defined:
These two sequences converge to the same number, which is the arithmetic-geometric mean of x and y; it is denoted by M(x, y), or sometimes by agm(x, y).
This can be used for algorithmic purposes as in the AGM method.
Contents |
Example
To find the arithmetic-geometric mean of a0 = 24 and g0 = 6, first calculate their arithmetic mean and geometric mean, thus:
and then iterate as follows:
etc.
The first four iterations give the following values:
-
n an gn 0 24 6 1 15 12 2 13.5 13.41640786500... 3 13.45820393250... 13.45813903099... 4 13.45817148175... 13.45817148171...
The arithmetic-geometric mean of 24 and 6 is the common limit of these two sequences, which is approximately 13.45817148173.
Properties
The geometric mean of two positive numbers is never bigger than the arithmetic mean (see inequality of arithmetic and geometric means); as a consequence, (gn) is an increasing sequence, (an) is a decreasing sequence, and gn ≤ M(x, y) ≤ an. These are strict inequalities if x ≠ y.
M(x, y) is thus a number between the geometric and arithmetic mean of x and y; in particular it is between x and y.
If r ≥ 0, then M(rx,ry) = rM(x,y).
There is an integral-form expression for M(x,y):
where K(m) is the complete elliptic integral of the first kind:
Indeed, since the arithmetic-geometric process converges so quickly, it provides an effective way to compute elliptic integrals via this formula.
The reciprocal of the arithmetic-geometric mean of 1 and the square root of 2 is called Gauss's constant.
named after Carl Friedrich Gauss.
The geometric-harmonic mean can be calculated by an analogous method, using sequences of geometric and harmonic means. The arithmetic-harmonic mean can be similarly defined, but takes the same value as the geometric mean.
Proof of existence
From inequality of arithmetic and geometric means we can conclude that:
and thus
that is, the sequence gi is nondecreasing.
Furthermore, it is easy to see that it is also bounded above by the larger of x and y (which follows from the fact that both arithmetic and geometric means of two numbers both lie between them). Thus by the monotone convergence theorem the sequence is convergent, so there exists a g such that:
However, we can also see that:
and so:
See also
References
- Jonathan Borwein, Peter Borwein, Pi and the AGM. A study in analytic number theory and computational complexity. Reprint of the 1987 original. Canadian Mathematical Society Series of Monographs and Advanced Texts, 4. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York, 1998. xvi+414 pp. ISBN 0-471-31515-X MR1641658
- Zoltán Daróczy, Zsolt Páles, Gauss-composition of means and the solution of the Matkowski-Suto problem. Publ. Math. Debrecen 61/1-2 (2002), 157–218.
- M. Hazewinkel (2001), "Arithmetic-geometric mean process", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=a/a130280
- Weisstein, Eric W., "Arithmetic-Geometric mean" from MathWorld.
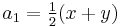
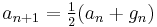
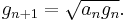
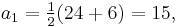
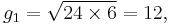
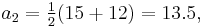
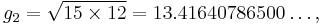
![\Mu(x,y) = \frac{\pi}{4} (x %2B y) \; / \; K\!\left[\left( \frac{x - y}{x %2B y} \right)^2 \right]](/2012-wikipedia_en_all_nopic_01_2012/I/209bd67258d06261697c43605ec71822.png)