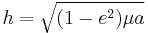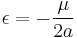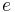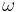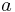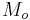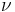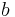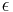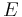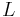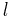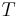Apsis
An apsis (Greek ἁψίς, gen. ἁψίδος), plural apsides ( /ˈæpsɨdiːz/; Greek: ἁψίδες), is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system. Historically, in geocentric systems, apsides were measured from the center of the Earth.
The point of closest approach (the point at which two bodies are the closest) is called the periapsis or pericentre, from Greek περί, peri, around, and κέντρον kentron. The point of farthest excursion is called the apoapsis (ἀπό, apó, "from", apocentre or apapsis [from ἀπ-, ap-, before an unaspirated, or ἀφ-, aph-, before an aspirated vowel, respectively]), (the latter term, although etymologically more correct, is much less used). A straight line drawn through the periapsis and apoapsis is the line of apsides. This is the major axis of the ellipse, the line through the longest part of the ellipse.
Derivative terms are used to identify the body being orbited. The most common are perigee /ˈpɛrɨdʒiː/ and apogee /ˈæpɵdʒiː/, referring to orbits around the Earth (Greek γῆ, gê, "earth"), and perihelion /ˌpɛrɨˈhiːliən/ and aphelion /əˈfiːliən/, referring to orbits around the Sun (Greek ἥλιος, hēlios, "sun"). During the Apollo program, the terms pericynthion and apocynthion were used when referring to the Moon.[1]
Contents |
Mathematical formulas
These formulas characterize the periapsis and apoapsis of an orbit:
- Periapsis: maximum speed
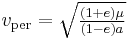 at minimum (periapsis) distance
at minimum (periapsis) distance 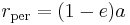
- Apoapsis: minimum speed
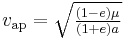 at maximum (apoapsis) distance
at maximum (apoapsis) distance 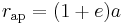
while, in accordance with Kepler's laws of planetary motion (based on the conservation of angular momentum) and the conservation of energy, these two quantities are constant for a given orbit:
where:
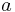 is the semi-major axis
is the semi-major axis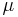 is the standard gravitational parameter
is the standard gravitational parameter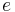 is the eccentricity, defined as
is the eccentricity, defined as 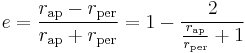
Note that for conversion from heights above the surface to distances between an orbit and its primary, the radius of the central body has to be added, and conversely.
The arithmetic mean of the two limiting distances is the length of the semi-major axis  . The geometric mean of the two distances is the length of the semi-minor axis
. The geometric mean of the two distances is the length of the semi-minor axis  .
.
The geometric mean of the two limiting speeds is 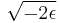 , the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocity).
, the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocity).
Terminology
The words "pericenter" and "apocenter" are occasionally seen, although periapsis/apoapsis are preferred in technical usage.
Various related terms are used for other celestial objects. The '-gee', '-helion' and '-astron' and '-galacticon' forms are frequently used in the astronomical literature, while the other listed forms are occasionally used, although '-saturnium' has very rarely been used in the last 50 years. The '-gee' form is commonly (although incorrectly) used as a generic 'closest approach to planet' term instead of specifically applying to the Earth. The term peri/apomelasma (from the Greek root) was used by physicist Geoffrey A. Landis in 1998 before peri/aponigricon (from the Latin) appeared in the scientific literature in 2002.[2]
| Body | Closest approach | Farthest approach |
|---|---|---|
| General | Periapsis/Pericentre | Apoapsis |
| Galaxy | Perigalacticon | Apogalacticon |
| Star | Periastron | Apastron |
| Black hole | Perimelasma/Peribothra/Perinigricon | Apomelasma/Apobothra/Aponigricon |
| Sun | Perihelion | Aphelion |
| Mercury | Perihermion | Apohermion |
| Venus | Pericytherion/Pericytherean/Perikrition | Apocytherion/Apocytherean/Apokrition |
| Earth | Perigee | Apogee |
| Moon | Periselene/Pericynthion/Perilune | Aposelene/Apocynthion/Apolune |
| Mars | Periareion | Apoareion |
| Jupiter | Perizene/Perijove | Apozene/Apojove |
| Saturn | Perikrone/Perisaturnium | Apokrone/Aposaturnium |
| Uranus | Periuranion | Apouranion |
| Neptune | Periposeidion | Apoposeidion |
| Pluto | Perihadion | Apohadion |
Since "peri" and "apo" are Greek, it is considered by some purists[3] more correct to use the Greek form for the body, giving forms such as '-zene' for Jupiter and '-krone' for Saturn. The daunting prospect of having to maintain a different word for every orbitable body in the Solar System (and beyond) is the main reason why the generic '-apsis' has become the almost universal norm in cases other than the Sun and Earth.
- In the Moon's case, in practice all three forms are used, albeit very infrequently. The '-cynthion' form (from the moon goddess Artemis' Ancient Greek epithet "Cynthia")[4] is, according to some, reserved for artificial bodies, whilst others reserve '-lune' for an object launched from the Moon and '-cynthion' for an object launched from elsewhere. The '-cynthion' form was the version used in the Apollo Project, following a NASA decision in 1964.
- For Venus, the form '-cytherion' is derived from the commonly used adjective 'cytherean'; the alternate form '-krition' (from Kritias, an older name for Aphrodite) has also been suggested.
- For Jupiter, the '-jove' form is occasionally used by astronomers whilst the '-zene' form is never used, like the other pure Greek forms ('-areion' (Mars), '-hermion' (Mercury), '-krone' (Saturn), '-uranion' (Uranus), '-poseidion' (Neptune) and '-hadion' (Pluto)).
The perihelion and aphelion of the Earth
For the orbit of the Earth around the sun, the time of apsis is often expressed in terms of a time relative to seasons, since this determines the contribution of the elliptical orbit to seasonal variations. The variation of the seasons is primarily controlled by the annual cycle of the elevation angle of the sun, which is a result of the tilt of the axis of the Earth measured from the plane of the ecliptic.
Currently, the annual perihelion happens at about 14 days after the December Solstice, thus on or about January 4. At perihelion, the Earth is about 0.98329 astronomical units (AU) or 147,098,070 kilometers (about 91,402,500 miles) from the sun. (The eccentricity of the orbit also varies slowly over many millennia.)
Likewise, the annual aphelion currently occurs in early July, about 14 days after the June Solstice. At this time, the distance of the aphelion is currently about 1.01671 AU or 152,097,700 kilometers (94,509,100 mi).
On a very long time scale, the dates of the perihelion and of the aphelion progress through the seasons, and they make one complete cycle in 22,000 to 26,000 years. There is a corresponding movement of the position of the stars as seen from Earth that is called the apsidal precession. (This is not the precession of the axis.)
Astronomers commonly express the timing of perihelion relative to the vernal equinox not in terms of days and hours, but rather as an angle of orbital displacement, the so-called longitude of the periapsis. For the orbit of the Earth, this is called the longitude of perihelion, and in the year 2000 was about 282.895 degrees. By the year 2010, this had advanced by a small fraction of a degree to about 283.067 degrees.[5]
The dates and times of the perihelions and aphelions for several past and future years are listed in the following table:[6]
| Year | Perihelion | Aphelion | ||
|---|---|---|---|---|
| Date | Hour[A] (UT) | Date | Hour[A] (UT) | |
| 2007 | January 3 | 20 | July 7 | 00 |
| 2008 | January 3 | 00 | July 4 | 08 |
| 2009 | January 4 | 15 | July 4 | 02 |
| 2010 | January 3 | 00 | July 6 | 12 |
| 2011 | January 3 | 19 | July 4 | 15 |
| 2012 | January 5 | 01 | July 5 | 04 |
| 2013 | January 2 | 05 | July 5 | 15 |
| 2014 | January 4 | 12 | July 4 | 00 |
| 2015 | January 4 | 07 | July 6 | 20 |
| 2016 | January 2 | 23 | July 4 | 16 |
| 2017 | January 4 | 14 | July 3 | 20 |
| 2018 | January 3 | 06 | July 6 | 17 |
| 2019 | January 3 | 05 | July 4 | 22 |
| 2020 | January 5 | 08 | July 4 | 12 |
Planetary perihelion and aphelion
The following table shows the distances of the planets and dwarf planets from the Sun at their perihelion and aphelion.[7]
| Type of body | Body | Distance from Sun at perihelion | Distance from Sun at aphelion |
|---|---|---|---|
| Planet | Mercury | 46,001,009 km (28,583,702 mi) | 69,817,445 km (43,382,549 mi) |
| Venus | 107,476,170 km (66,782,600 mi) | 108,942,780 km (67,693,910 mi) | |
| Earth | 147,098,291 km (91,402,640 mi) | 152,098,233 km (94,509,460 mi) | |
| Mars | 206,655,215 km (128,409,597 mi) | 249,232,432 km (154,865,853 mi) | |
| Jupiter | 740,679,835 km (460,237,112 mi) | 816,001,807 km (507,040,016 mi) | |
| Saturn | 1,349,823,615 km (838,741,509 mi) | 1,503,509,229 km (934,237,322 mi) | |
| Uranus | 2,734,998,229 km (1.699449110×109 mi) | 3,006,318,143 km (1.868039489×109 mi) | |
| Neptune | 4,459,753,056 km (2.771162073×109 mi) | 4,537,039,826 km (2.819185846×109 mi) | |
| Dwarf planet | Ceres | 380,951,528 km (236,712,305 mi) | 446,428,973 km (277,398,103 mi) |
| Pluto | 4,436,756,954 km (2.756872958×109 mi) | 7,376,124,302 km (4.583311152×109 mi) | |
| Makemake | 5,671,928,586 km (3.524373028×109 mi) | 7,894,762,625 km (4.905578065×109 mi) | |
| Haumea | 5,157,623,774 km (3.204798834×109 mi) | 7,706,399,149 km (4.788534427×109 mi) | |
| Eris | 5,765,732,799 km (3.582660263×109 mi) | 14,594,512,904 km (9.068609883×109 mi) |
The following chart shows the range of distances of the planets, dwarf planets and Halley's Comet from the Sun.

Range of selected bodies of the Solar System from the middle of the Sun. The left and right edges of each bar correspond to the perihelion and aphelion of the body, respectively. Long bars denote high orbital eccentricity.
The images below show the perihelion and aphelion points of the inner and outer planets.
See also
Notes and references
- ^ The source data is specific only to the hour.
- ^ "Apollo 15 Mission Report". Glossary. http://history.nasa.gov/alsj/a15/a15mr-f.htm. Retrieved October 16, 2009.
- ^ R. Schodel, T. Ott, R. Genzel, R. Hofmann, M. Lehnert, A. Eckart, N. Mouawad, T. Alexander, M.J. Reid, R. Lenzen, M. Hartung, F. Lacombe, D. Rouan, E. Gendron, G. Rousset, A.-M. Lagrange, W. Brandner, N. Ageorges, C. Lidman, A.F.M. Moorwood, J. Spyromilio, N. Hubin, and K.M. Menten, "Closest Star Seen Orbiting the Supermassive Black Hole at the Centre of the Milky Way," Nature 419, 694-696 (17 October 2002), doi:10.1038/nature01121.
- ^ "Apsis". Glossary of Terms. National Solar Observatory. 2005-02-21. http://www.nso.edu/press/glossary.html#apsis. Retrieved 2006-09-30.
- ^ Merriam–Webster "pericynthion"
- ^ NASA.gov
- ^ Earth's Seasons: Equinoxes, Solstices, Perihelion, and Aphelion - 2000-2020 —U.S. Naval Observatory, Astronomical Applications Department (accessed 2010-07-06).
- ^ NASA planetary comparison chart http://solarsystem.nasa.gov/planets/compchart.cfm
External links
- Apogee - Perigee Photographic Size Comparison, perseus.gr
- Aphelion - Perihelion Photographic Size Comparison, perseus.gr
- Earth's Seasons: Equinoxes, Solstices, Perihelion, and Aphelion, 2000-2020, usno.navy.mil