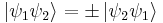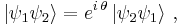Anyon

Not to be confused with anion, a negatively-charged ion.
Statistical mechanics
Thermodynamics · Kinetic theory
Particle Statistics
Spin-Statistics Theorem
Identical Particles
Maxwell–Boltzmann
Bose–Einstein · Fermi–Dirac
Parastatistics · Anyonic Statistics
Braid Statistics

In physics, an anyon is a type of particle that occurs only in two-dimensional systems. It is a generalization of the fermion and boson concept.

Contents

From theory to reality

A group of theoretical physicists working at the University of Oslo, led by Jon Leinaas and Jan Myrheim, calculated in 1977 that the traditional division between fermions and bosons would not apply to theoretical particles existing in two dimensions.[1] Such particles would be expected to exhibit a diverse range of previously unexpected properties. They were given the name anyons by Frank Wilczek in 1982.[2] The associated mathematics proved to be useful to Bertrand Halperin at Harvard University in explaining aspects of the fractional quantum Hall effect. Frank Wilczek, Dan Arovas, and Robert Schrieffer verified this statement in 1985 with an explicit calculation that predicted that particles existing in these systems are in fact anyons.

In 2005 a group of physicists at Stony Brook University constructed a quasiparticle interferometer, detecting the patterns caused by interference of anyons which were interpreted to suggest that anyons are real, rather than just a mathematical construct.[3] However, these experiments remain controversial and are not fully accepted by the community.

With developments in semiconductor technology meaning that the deposition of thin two-dimensional layers is possible – for example in sheets of graphene – the long term potential to use the properties of anyons in electronics is being explored.

In physics

In space of three or more dimensions, indistinguishable particles are restricted to being Fermions or Bosons, according to their statistical behaviour. Fermions respect the so-called Fermi–Dirac statistics while Bosons respect the Bose–Einstein statistics. In the language of quantum physics this is formulated as the behavior of multiparticle states under the exchange of particles. This is in particular for a two-particle state (in Dirac notation):

\left|\psi_1\psi_2\right\rangle = \pm\left|\psi_2\psi_1\right\rangle

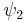(where the first entry in \left|\dots\right\rangle is the state of particle 1 and the second entry is the state of particle 2. So for example the left hand side is read as "Particle 1 is in state \ \psi_1 and particle 2 in state \ \psi_2"). Here the "+" corresponds to both particles being Bosons and the "−" to both particles being Fermions (composite states of Fermions and Bosons are irrelevant since that would make them distinguishable).

In two-dimensional systems, however, quasiparticles can be observed which obey statistics ranging continuously between Fermi–Dirac and Bose–Einstein statistics, as was first shown by Jon Magne Leinaas and Jan Myrheim of the University of Oslo in 1977.[4] In our above example of two particles this looks as follows:

\left|\psi_1\psi_2\right\rangle = e^{i\,\theta}\left|\psi_2\psi_1\right\rangle\,,

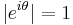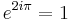with i being the imaginary unit and θ a real number. Recall that |e^{i\theta}|=1 and e^{2i\pi}=1 as well as 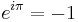e^{i\pi}=-1. So in the case 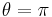\theta=\pi we recover the Fermi–Dirac statistics (minus sign) and in the case θ = 0 (or 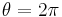\theta=2\pi) the Bose–Einstein statistics (plus sign). In between we have something different. Frank Wilczek coined the term "anyon"[5] to describe such particles, since they can have any phase when particles are interchanged.

We also may use 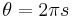\theta=2 \pi s\; with particle spin quantum number s, with s being integer for Bosons, half-integer for Fermions, so that

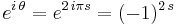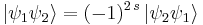e^{i\,\theta} = e^{2\,i \pi s} = (-1)^{2\,s}   or   \left|\psi_1\psi_2\right\rangle = (-1)^{2\,s}\left|\psi_2\psi_1\right\rangle.

At an edge, fractional quantum Hall effect anyons are confined to move in one space dimension. Mathematical models of one dimensional anyons provide a base of the commutation relations shown above.

Just as how the Fermion and Boson wavefunctions in a three dimensional space are just 1-dimensional representations of the Permutation group (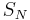S_{N} of N indistinguishable particles), the anyonic wavefunctions in a two dimensional space are just 1-dimensional representations of the Braid group (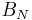B_{N} of N indistinguishable particles). Please note that anyonic statistics must not be confused with parastatistics which describes statistics of particles whose wavefunctions are higher dimensional representations of the permutation group.[6]

Topological basis

In more than two dimensions, the spin-statistics connection states that any multiparticle state has to obey either Bose–Einstein or Fermi–Dirac statistics. For any d>2, the group SO(d,1) (which generalize the Lorentz group), and also Poincaré(d,1), have 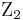\mathrm{Z}_2 as their first homotopy group. 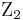\mathrm{Z}_2 is the cyclic group consisting of two elements, therefore only two possibilities remain. (The details are more involved than that, but this is the crucial point.)

The situation changes in two dimensions. Here the first homotopy group of SO(2,1), and also Poincaré(2,1), is Z (infinite cyclic). This means that Spin(2,1) is not the universal cover: it is not simply connected. In detail, there are projective representations of the special orthogonal group SO(2,1) which do not arise from linear representations of SO(2,1), or of its double cover, the spin group Spin(2,1). These representations are called anyons.

This concept also applies to nonrelativistic systems. The relevant part here is that the spatial rotation group is SO(2) has an infinite first homotopy group.

This fact is also related to the braid groups well known in knot theory. The relation can be understood when one considers the fact that in two dimensions the group of permutations of two particles is no longer the symmetric group 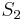S_2 (with two elements) but rather the braid group 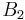B_2 (with an infinite number of elements). The essential point is that one braid can wind around the other one, an operation that can be performed infinitely often, and clockwise as well as counterclockwise.

A very different approach to the stability-decoherence problem in quantum computing is to create a topological quantum computer with anyons, quasi-particles used as threads and relying on braid theory to form stable logic gates.[7][8]

See also

References

  1. ^ Wilczek, Frank (January 2006). "From electronics to anyonics". Physics World. ISSN 0953-8585. http://physicsworld.com/cws/article/indepth/23894. 
  2. ^ "Frank Wilczek on anyons and their Role in Superconductivity". Science Watch. http://www.sciencewatch.com/interviews/frank_wilczek1.htm. 
  3. ^ Camino, F.; Zhou, Wei; Goldman, V. (2005). "Realization of a Laughlin quasiparticle interferometer: Observation of fractional statistics". Physical Review B 72 (7). arXiv:cond-mat/0502406. Bibcode 2005PhRvB..72g5342C. doi:10.1103/PhysRevB.72.075342. 
  4. ^ Leinaas, J.M.; J. Myrheim (11 January 1977). "On the theory of identical particles". Il Nuovo Cimento B 37 (1): 1–23. Bibcode 1977NCimB..37....1L. doi:10.1007/BF02727953. 
  5. ^ Wilczek, Frank (4 October 1982). "Quantum Mechanics of Fractional-Spin Particles". Physical Review Letters 49 (14): 957–959. Bibcode 1982PhRvL..49..957W. doi:10.1103/PhysRevLett.49.957. 
  6. ^ Khare, Avinash (2005). Fractional Statistics and Quantum Theory. World Scientific. p. 22. ISBN 9812561609, 9789812561602. http://books.google.com/?id=rBi7zTpvjaAC&dq=Fractional+Statistics+and+Quantum+Theory. Retrieved May, 2011. 
  7. ^ Freedman, Michael; Alexei Kitaev, Michael Larsen, Zhenghan Wang (20 October 2002). "Topological Quantum Computation". Bulletin of the American Mathematical Society 40 (1): 31–38. doi:10.1090/S0273-0979-02-00964-3. 
  8. ^ Monroe, Don (1 October 2008). "Anyons: The breakthrough quantum computing needs?". New Scientist (2676). http://www.newscientist.com/channel/fundamentals/mg20026761.700-anyons-the-breakthrough-quantum-computing-needs.html. 

Further reading