Antihomomorphism

In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to itself.

1 Definition
2 Examples
- 2.1 Involutions
3 Properties
4 See also
5 References

Definition

Informally, an antihomomorphism is map that switches the order of multiplication.

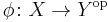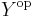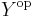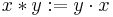Formally, an antihomomorphism between X and Y is a homomorphism $\phi\colon X \to Y^{\text{op}}$ , where $Y^{\text{op}}$ equals Y as a set, but has multiplication reversed: denoting the multiplication on Y as $\cdot$ and the multiplication on $Y^{\text{op}}$ as $*$ , we have $x*y�:= y\cdot x$ . The object 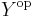$Y^{\text{op}}$ is called the opposite object to Y. (Respectively, opposite group, opposite algebra, etc.)

This definition is equivalent to a homomorphism 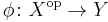$\phi\colon X^{\text{op}} \to Y$ (reversing the operation before or after applying the map is equivalent). Formally, sending X to 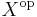$X^{\text{op}}$ and acting as the identity on maps is a functor (indeed, an involution).

Examples

In group theory, an antihomomorphism is a map between two groups that reverses the order of multiplication. So if φ : X → Y is a group antihomomorphism,

φ(xy) = φ(y)φ(x)

for all x, y in X.

The map that sends x to x⁻¹ is an example of a group antiautomorphism. Another important example is the transpose operation in linear algebra which takes row vectors to column vectors. Any vector-matrix equation may be transposed to an equivalent equation where the order of the factors is reversed.

In ring theory, an antihomomorphism is a map between two rings that preserves addition, but reverses the order of multiplication. So φ : X → Y is a ring antihomomorphism if and only if:

φ(1) = 1

φ(x+y) = φ(x)+φ(y)

φ(xy) = φ(y)φ(x)

for all x, y in X.

For algebras over a field K, φ must be a K-linear map of the underlying vector space. If the underlying field has an involution, one can instead ask φ to be conjugate-linear, as in conjugate transpose, below.

Involutions

It is frequently the case that antiautomorphisms are involutions, i.e. the square of the antiautomorphism is the identity map; these are also called involutive antiautomorphisms.

The map that sends x to its inverse x⁻¹ is an involutive antiautomorphism in any group.

A ring with an involutive antiautomorphism is called a *-ring, and these form an important class of examples.

Properties

If the target Y is commutative, then an antihomomorphism is the same thing as a homomorphism and an antiautomorphism is the same thing as an automorphism.

The composition of two antihomomorphisms is always a homomorphism, since reversing the order twice preserves order. The composition of an antihomomorphism with a homomorphism gives another antihomomorphism.

References

Weisstein, Eric W., "Antihomomorphism" from MathWorld.