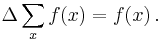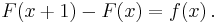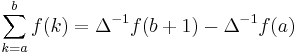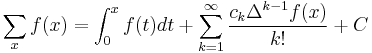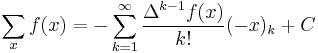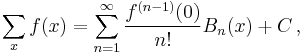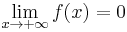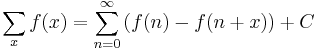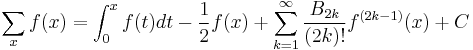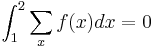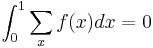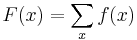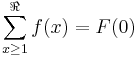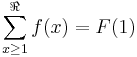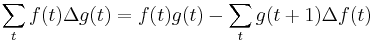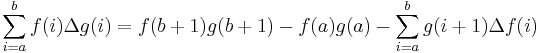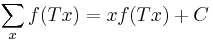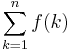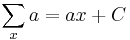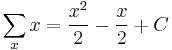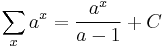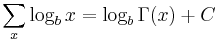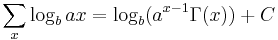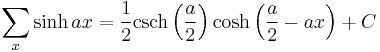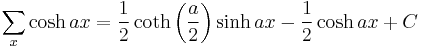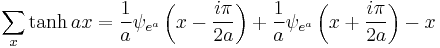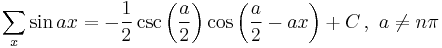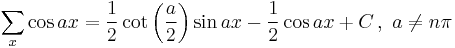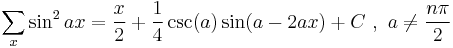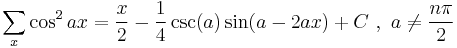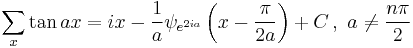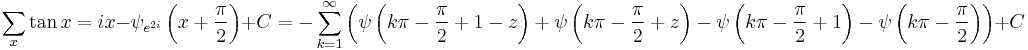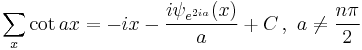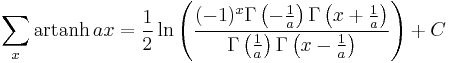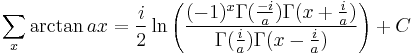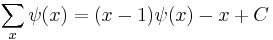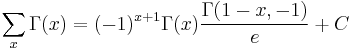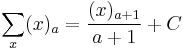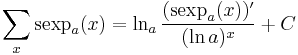Indefinite sum

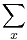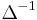In mathematics the indefinite sum operator (also known as the antidifference operator), denoted by $\sum _x \,$ or $\Delta^{-1} \,$ ,^[1]^[2]^[3] is the linear operator, inverse of the forward difference operator $\Delta \,$ . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus

$\Delta \sum_x f(x) = f(x) \, .$

More explicitly, if 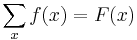$\sum_x f(x) = F(x) \,$ , then

$F(x%2B1) - F(x) = f(x) \, .$

If F(x) is a solution of this functional equation for a given f(x), then so is F(x)+C for any constant C. Therefore each indefinite sum actually represents a family of functions, differing by an additive constant.

Fundamental theorem of discrete calculus

Indefinite sums can be used to calculate definite sums with the formula^[4]:

$\sum_{k=a}^b f(k)=\Delta^{-1}f(b%2B1)-\Delta^{-1}f(a)$

Definitions

Laplace summation formula

$\sum _x f(x)=\int_0^x f(t) dt %2B\sum_{k=1}^\infty \frac{c_k\Delta^{k-1}f(x)}{k!} %2B C$

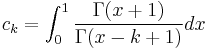where $c_k=\int_0^1 \frac{\Gamma(x%2B1)}{\Gamma(x-k%2B1)}dx$ are the Bernoulli numbers of the second kind.^[5]

Newton's formula

$\sum_x f(x)=-\sum_{k=1}^{\infty}\frac{\Delta^{k-1}f(x)}{k!}(-x)_k%2BC$

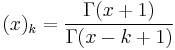where $(x)_k=\frac{\Gamma(x%2B1)}{\Gamma(x-k%2B1)}$ is the falling factorial.

Faulhaber's formula

$\sum _x f(x)= \sum_{n=1}^{\infty} \frac{f^{(n-1)} (0)}{n!} B_n(x) %2B C \, ,$

provided that the right-hand side of the equation converges.

Mueller's formula

$\lim_{x\to{%2B\infty}}f(x)=0$

then^[6]

$\sum _x f(x)=\sum_{n=0}^\infty\left(f(n)-f(n%2Bx)\right)%2B C$

Ramanujan's formula

$\sum _x f(x)= \int_0^x f(t) dt - \frac12 f(x)%2B\sum_{k=1}^{\infty}\frac{B_{2k}}{(2k)!}f^{(2k-1)}(x) %2B C$

Connection to the Ramanujan summation

Often the constant C in indefinite sum is fixed from the following equation:

$\int_1^2 \sum _x f(x) dx=0$

$\int_0^1 \sum _x f(x) dx=0$

In this case, where

$F(x)=\sum _x f(x) \,$

then Ramanjuan's sum is defined as

$\sum_{x \ge 1}^{\Re}f(x)=F(0)\,$

$\sum_{x \ge 1}^{\Re}f(x)=F(1)\,$ ^[7]^[8]

Summation by parts

Main article: Summation by parts

Indefinite summation by parts:

$\sum _t f(t)\Delta g(t)=f(t)g(t)-\sum _t g(t%2B1) \Delta f(t) \,$

Definite summation by parts:

$\sum_{i=a}^b f(i)\Delta g(i)=f(b%2B1)g(b%2B1)-f(a)g(a)-\sum_{i=a}^b g(i%2B1)\Delta f(i)$

Period rule

If 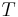$T \,$ is a period of function 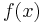$f(x)\,$ then

$\sum _x f(Tx)=x f(Tx) %2B C\,$

Alternative usage

Some authors use the phrase "indefinite sum" to describe a sum in which the numerical value of the upper limit is not given. e.g.

$\sum_{k=1}^n f(k)$

In this case a closed form expression F(k) for the sum is a solution of

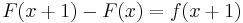$F(x%2B1) - F(x) = f(x%2B1) \,$ which is called the telescoping equation.^[9] It is inverse to backward difference 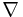$\nabla$ operator.

It is related to the forward antidifference operator using the fundamental theorem of discrete calculus described earlier.

List of indefinite sums

This is a list of indefinite sums of various functions. Not every function has an indefinite sum that can be expressed in terms of elementary functions.

Antidifferences of rational functions

$\sum _x a = ax %2B C \,$

$\sum _x x = \frac{x^2}{2}-\frac{x}{2} %2B C$

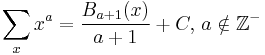
$\sum _x x^a = \frac{B_{a%2B1}(x)}{a%2B1} %2B C,\,a\notin \mathbb{Z}^-$

where 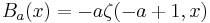$B_a(x)=-a\zeta(-a%2B1,x)\,$ , the generalized to real order Bernoulli polynomials.

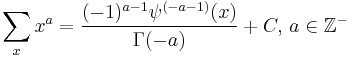
$\sum _x x^a = \frac{(-1)^{a-1}\psi^{(-a-1)}(x)}{\Gamma(-a)}%2B C,\,a\in\mathbb{Z}^-$

where 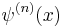$\psi^{(n)}(x)$ is the polygamma function.

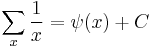
$\sum _x \frac1x = \psi(x) %2B C$

where 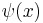$\psi(x)$ is the digamma function.

Antidifferences of exponential functions

$\sum _x a^x = \frac{a^x}{a-1} %2B C \,$

Antidifferences of logarithmic functions

$\sum _x \log_b x = \log_b \Gamma (x) %2B C \,$

$\sum _x \log_b ax = \log_b (a^{x-1}\Gamma (x)) %2B C \,$

Antidifferences of hyperbolic functions

$\sum _x \sinh ax = \frac{1}{2} \operatorname{csch} \left(\frac{a}{2}\right) \cosh \left(\frac{a}{2} - a x\right) %2B C \,$

$\sum _x \cosh ax = \frac{1}{2} \coth \left(\frac{a}{2}\right) \sinh ax -\frac{1}{2} \cosh ax %2B C \,$

$\sum _x \tanh ax = \frac1a \psi _{e^a}\left(x-\frac{i \pi }{2 a}\right)%2B\frac1a \psi _{e^a}\left(x%2B\frac{i \pi }{2 a}\right)-x$

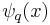where $\psi_q(x)$ is the q-digamma function.

Antidifferences of trigonometric functions

$\sum _x \sin ax = -\frac{1}{2} \csc \left(\frac{a}{2}\right) \cos \left(\frac{a}{2}- a x \right) %2B C \,,\,\,a\ne n \pi$

$\sum _x \cos ax = \frac{1}{2} \cot \left(\frac{a}{2}\right) \sin ax -\frac{1}{2} \cos ax %2B C \,,\,\,a\ne n \pi$

$\sum _x \sin^2 ax = \frac{x}{2} %2B \frac{1}{4} \csc (a) \sin (a-2 a x) %2B C \, \,,\,\,a\ne \frac{n\pi}2$

$\sum _x \cos^2 ax = \frac{x}{2}-\frac{1}{4} \csc (a) \sin (a-2 a x) %2B C \,\,,\,\,a\ne \frac{n\pi}2$

$\sum_x \tan ax = i x-\frac1a \psi _{e^{2 i a}}\left(x-\frac{\pi }{2 a}\right)%2B C \,,\,\,a\ne \frac{n\pi}2$

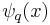where $\psi_q(x)$ is the q-digamma function.

$\sum_x \tan x=ix-\psi _{e^{2 i}}\left(x%2B\frac{\pi }{2}\right)%2BC = -\sum _{k=1}^{\infty } \left(\psi \left(k \pi -\frac{\pi }{2}%2B1-z\right)%2B\psi \left(k \pi -\frac{\pi }{2}%2Bz\right)-\psi \left(k \pi -\frac{\pi }{2}%2B1\right)-\psi \left(k \pi -\frac{\pi }{2}\right)\right)%2BC\,$

$\sum_x \cot ax =-i x-\frac{i \psi _{e^{2 i a}}(x)}{a} %2B C \,,\,\,a\ne \frac{n\pi}2$

Antidifferences of inverse hyperbolic functions

$\sum_x \operatorname{artanh}\, a x =\frac{1}{2} \ln \left(\frac{(-1)^x \Gamma \left(-\frac{1}{a}\right) \Gamma \left(x%2B\frac{1}{a}\right)}{\Gamma \left(\frac{1}{a}\right) \Gamma \left(x-\frac{1}{a}\right)}\right) %2B C$

Antidifferences of inverse trigonometric functions

$\sum_x \arctan a x = \frac{i}{2} \ln \left(\frac{(-1)^x \Gamma (\frac{-i}a) \Gamma (x%2B\frac ia)}{\Gamma (\frac ia) \Gamma (x-\frac ia)}\right)%2BC$

Antidifferences of special functions

$\sum _x \psi(x)=(x-1) \psi(x)-x%2BC \,$

$\sum _x \Gamma(x)=(-1)^{x%2B1}\Gamma(x)\frac{\Gamma(1-x,-1)}e%2BC$

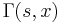where $\Gamma(s,x)$ is the incomplete gamma function.

$\sum _x (x)_a = \frac{(x)_{a%2B1}}{a%2B1}%2BC$

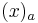where $(x)_a$ is the falling factorial.

$\sum _x \operatorname{sexp}_a (x) = \ln_a \frac{(\operatorname{sexp}_a (x))'}{(\ln a)^x} %2B C \,$

(see super-exponential function)

References

^ Indefinite Sum at PlanetMath.
^ On Computing Closed Forms for Indefinite Summations. Yiu-Kwong Man. J. Symbolic Computation (1993), 16, 355-376
^ "If Y is a function whose first difference is the function y, then Y is called an indefinite sum of y and denoted Δ^-1y" Introduction to Difference Equations, Samuel Goldberg
^ "Handbook of discrete and combinatorial mathematics", Kenneth H. Rosen, John G. Michaels, CRC Press, 1999, ISBN 0849301491
^ Bernoulli numbers of the second kind on Mathworld
^ Markus Müller. How to Add a Non-Integer Number of Terms, and How to Produce Unusual Infinite Summations (note that he uses a slightly alternative definition of fractional sum in his work, i.e. inverse to backwards difference, hence 1 as the lower limit in his formula)
^ Bruce C. Berndt, Ramanujan's Notebooks, Ramanujan's Theory of Divergent Series, Chapter 6, Springer-Verlag (ed.), (1939), pp. 133–149.
^ Éric Delabaere, Ramanujan's Summation, Algorithms Seminar 2001–2002, F. Chyzak (ed.), INRIA, (2003), pp. 83–88.
^ Algorithms for Nonlinear Higher Order Difference Equations, Manuel Kauers