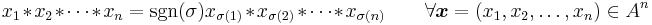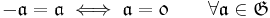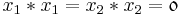Anticommutativity
In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric operations.
Contents |
Definition
An  -ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation * is anti-commutative if for all x and y, x*y = −y*x.
-ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation * is anti-commutative if for all x and y, x*y = −y*x.
More formally, a map 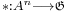 from the set of all n-tuples of elements in a set A (where n is a general integer) to a group
from the set of all n-tuples of elements in a set A (where n is a general integer) to a group 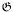 is anticommutative if and only if
is anticommutative if and only if
where 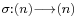 is an arbitrary permutation of the set (n) of the first n non-zero integers and
is an arbitrary permutation of the set (n) of the first n non-zero integers and 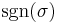 is its sign. This equality expresses the following concept:
is its sign. This equality expresses the following concept:
- the value of the operation is unchanged, when applied to all ordered tuples constructed by even permutation of the elements of a fixed one.
- the value of the operation is the inverse of its value on a fixed tuple, when applied to all ordered tuples constructed by odd permutation to the elements of the fixed one. The need for the existence of this inverse element is the main reason for requiring the codomain
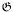 of the operation to be at least a group.
of the operation to be at least a group.
Note that this is an abuse of notation, since the codomain of the operation needs only to be a group: "−1" does not have a precise meaning since a multiplication is not necessarily defined on 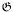 .
.
Particularly important is the case n=2. A binary operation 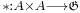 is anticommutative if and only if
is anticommutative if and only if
This means that 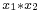 is the inverse of the element
is the inverse of the element 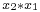 in
in 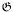 .
.
Properties
If the group 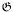 is such that
is such that
i.e. the only element equal to its inverse is the neutral element, then for all the ordered tuples such that 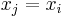 for at least two different index
for at least two different index 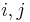
In the case 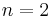 this means
this means
Examples
Anticommutative operators include:
See also
- Commutativity
- Commutator
- Exterior algebra
- Operation (mathematics)
- Symmetry in mathematics
- Particle statistics (for anticommutativity in physics).
References
- Bourbaki, Nicolas (1989), "Chapter III. Tensor algebras, exterior algebras, symmetric algebras", Algebra. Chapters 1–3, Elements of Mathematics (2nd printing ed.), Berlin-Heidelberg-New York: Springer-Verlag, pp. xxiii+709, ISBN 3-540-64243-9, MR0979982, Zbl 0904.00001.
External links
- Gainov, A.T. (2001), "Anti-commutative algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=A/a012580
- Weisstein, Eric W., "Anticommutative" from MathWorld.