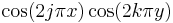Spatial anti-aliasing

In digital signal processing, spatial anti-aliasing is the technique of minimizing the distortion artifacts known as aliasing when representing a high-resolution image at a lower resolution. Anti-aliasing is used in digital photography, computer graphics, digital audio, and many other applications.

Anti-aliasing means removing signal components that have a higher frequency than is able to be properly resolved by the recording (or sampling) device. This removal is done before (re)sampling at a lower resolution. When sampling is performed without removing this part of the signal, it causes undesirable artifacts such as the black-and-white noise near the top of figure 1-a below.

In signal acquisition and audio, anti-aliasing is often done using an analog anti-aliasing filter to remove the out-of-band component of the input signal prior to sampling with an analog-to-digital converter. In digital photography, optical anti-aliasing filters are made of birefringent materials, and smooth the signal in the spatial optical domain. The anti-aliasing filter essentially blurs the image slightly in order to reduce resolution to below the limit of the digital sensor (the larger the pixel pitch, the lower the achievable resolution at the sensor level).

See the articles on signal processing and aliasing for more information about the theoretical justifications for anti-aliasing.

Contents

Examples

(a)
(b)
(c)
Figure 1

In computer graphics, anti aliasing improves the appearance of polygon edges, so they are not "jagged", but smoothed out on the screen. However, it incurs a performance cost for the graphics card and uses more video memory. The level of anti-aliasing determines how smooth polygon edges are (and how much video memory it consumes).

Figure 1-a illustrates the visual distortion that occurs when anti-aliasing is not used. Notice that near the top of the image, where the checkerboard is very distant, the image is difficult to recognize and is not aesthetically appealing. In contrast, Figure 1-b shows an anti-aliased version of the scene. The checkerboard near the top blends into gray, which is usually the desired effect when the resolution is insufficient to show the detail. Even near the bottom of the image, the edges appear much smoother in the anti-aliased image. Figure 1-c shows another anti-aliasing algorithm, based on the sinc filter, which is considered better than the algorithm used in 1-b.[1]

Figure 2 shows magnified portions (interpolated with nearest neighbor algorithm) of Figure 1-a (left) and 1-c (right) for comparison. In Figure 1-c, anti-aliasing has interpolated the brightness of the pixels at the boundaries to produce gray pixels since the space is occupied by both black and white tiles. These help make Figure 1-c appear much smoother than Figure 1-a at original magnification.

In Figure 3, anti-aliasing was used to blend the boundary pixels of a sample graphic. This reduced the aesthetically jarring effect of the sharp, step-like boundaries that appear in the aliased graphic at the left. Anti-aliasing is often applied in rendering text on a computer screen to suggest smooth contours that better emulate the appearance of text produced by conventional ink-and-paper printing.

Particularly with fonts displayed on typical LCD screens, it is common to use subpixel rendering techniques like ClearType. Subpixel rendering requires special color-balanced anti-aliasing filters to turn what would be severe color distortion into barely-noticeable color fringes. Equivalent results can be had by making individual subpixels addressable as if they were full pixels, and supplying a hardware-based anti-aliasing filter as is done in the OLPC XO-1 laptop's display controller. Pixel geometry affects all of this, no matter if the anti-aliasing and subpixel addressing are done in software or hardware.

Above left: an aliased version of a simple shape. Above right: an anti-aliased version of the same shape. Right: The anti-aliased graphic at 5x magnification.
Figure 3

Signal processing approach to anti-aliasing

In this approach, the ideal image is regarded as a signal. The image displayed on the screen is taken as samples, at each (x,y) pixel position, of a filtered version of the signal. Ideally, we would understand how the human brain would process the original signal, and provide an image on screen that will yield the most similar response by the brain.

The most widely accepted analytic tool for such problems is the Fourier transform. The Fourier transform decomposes a signal into basis functions of different frequencies, known as frequency components, and gives us the amplitude of each frequency component in the signal. The waves are of the form:

\ \cos (2j \pi x) \cos (2k \pi y)

where j and k are arbitrary non-negative integers. There are also frequency components involving the sine functions in one or both dimensions, but for the purpose of this discussion, the cosine will suffice; see Fourier transform for technical details.

The numbers j and k together are the frequency of the component: j is the frequency in the x direction, and k is the frequency in the y direction.

The goal of an anti-aliasing filter is to greatly reduce frequencies above a certain limit, known as the Nyquist frequency, so that the signal will be accurately represented by its samples, or nearly so, in accordance with the sampling theorem; there are many different choices of detailed algorithm, with different filter transfer functions. Our knowledge of human visual perception is not sufficient, in general, to say what approach will look best.

Two dimensional considerations

The above assumes that the rectangular mesh sampling is the dominant part of the problem. It should seem odd that the filter usually considered optimal is not rotationally symmetrical, as shown in this first figure. This is due to the fact that we are dealing with data sampled on a square lattice and not with a continuous image. This must be the justification for doing signal processing, along each axis, as it is traditionally done on one dimensional data. Lanczos resampling is based on convolution of the data with a discrete representation of the sinc function.

If the resolution is not limited by the rectangular sampling rate of either the source or the target image, then one should ideally use rotationally symmetrical filter or interpolation functions, as though the data were a two dimensional function of continuous x and y. The sinc function of the radius, in the second figure, has too long a tail to make a good filter (it is not even square-integrable). A more appropriate analog to the one-dimensional sinc is the two-dimensional Airy disc amplitude, the 2D Fourier transform of a circular region in 2D frequency space, as opposed to a square region.

One might consider a Gaussian plus enough of its second derivative to flatten the top (in the frequency domain) or sharpen it up (in the spatial domain). This function is shown also. Functions based on the Gaussian function are natural choices, because convolution with a Gaussian gives another Gaussian, whether applied to x and y or to the radius. Similar to wavelets, another of its properties is that it is half way between being localized in the configuration (x and y) and in the spectral (j and k) representation. As an interpolation function, a Gaussian alone seems too spread out to preserve the maximum possible detail, which is why the second derivative is added.

As an example, when printing a photographic negative, with plentiful processing capability, on a printer with a hexagonal pattern, there is no reason to use sinc function interpolation. This would treat diagonal lines differently from horizontal and vertical lines, which is like a weak form of aliasing.

Practical real-time anti-aliasing approximations

There are only a handful of primitives used at the lowest level in a real-time rendering engine (either software or hardware accelerated.) These include "points", "lines" and "triangles". If one is to draw such a primitive in white against a black background, it is possible to design such a primitive to have fuzzy edges, achieving some sort of anti-aliasing. However, this approach has difficulty dealing with adjacent primitives (such as triangles that share an edge.)

To approximate the uniform averaging algorithm, one may use an extra buffer for sub-pixel data. The initial, and least memory-hungry approach, used 16 extra bits per pixel, in a 4×4 grid. If one renders the primitives in a careful order, for instance front-to-back, it is possible to create a reasonable image.

Since this requires that the primitives be in some order, and hence interacts poorly with an application programming interface such as OpenGL, the latest attempts simply have two or more full sub-pixels per pixel, including full color information for each sub-pixel. Some information may be shared between the sub-pixels (such as the Z-buffer.)

Mipmapping

Main article: Mipmap

There is also an approach specialized for texture mapping called mipmapping, which works by creating lower resolution, prefiltered versions of the texture map. When rendering the image, the appropriate resolution mip-map is chosen and hence the texture pixels (texels) are already filtered when they arrive on the screen. Mipmapping is generally combined with various forms of texture filtering in order to improve the final result.

An example of an image with extreme pseudo-random aliasing

Because fractals have unlimited detail and no noise other than arithmetic roundoff error, they illustrate aliasing more clearly than do photographs or other measured data. The dwells, which are converted to colors at the exact centers of the pixels, go to infinity at the border of the set, so colors from centers near borders are unpredictable, due to aliasing. This example has edge in about half of its pixels, so it shows much aliasing. The first image is uploaded at its original sampling rate. Since most modern software anti-aliases, one may have to download the full size version to see all of the aliasing. The second image is calculated at five times the sampling rate and down-sampled with anti-aliasing. Assuming that we would really like something like the average color over each pixel, this one is getting closer. It is clearly more orderly than the first.

In order to properly compare these images, click to view them in their original sizes.

It happens that, in this case, there is additional information that can be used. By re-calculating with the distance estimator, points were identified that are very close to the edge of the set, so that unusually fine detail is aliased in from the rapidly changing dwell values near the edge of the set. The colors derived from these calculated points have been identified as unusually unrepresentative of their pixels. Those points were replaced, in the third image, by interpolating the points around them. This reduces the noisiness of the image but has the side effect of brightening the colors. So this image is not exactly the same that would be obtained with an even larger set of calculated points.

To show what was discarded, the rejected points, bled into a grey background, are shown in the fourth image.

Finally, "Budding Turbines" is so regular that systematic (Moiré) aliasing can clearly be seen near the main "turbine axis" when it is downsized by taking the nearest pixel. The aliasing in the first image appears random because it comes from all levels of detail, below the pixel size. When the lower level aliasing is suppressed, to make the third image and then that is down-sampled once more, without anti-aliasing, to make the fifth image, the order on the scale of the third image appears as systematic aliasing in the fifth image.

The best anti-aliasing and down-sampling method here depends on one's point of view. When fitting the most data into a limited array of pixels, as in the fifth image, sinc function anti-aliasing would seem appropriate. In obtaining the second and third images, the main objective is to filter out aliasing "noise", so a rotationally symmetrical function may be more appropriate.

Pure down-sampling of an image has the following effect: (Click on each picture to see it at full scale)

Super sampling / full-scene anti-aliasing

Super sampling anti-aliasing (SSAA),[2] also called full-scene anti-aliasing (FSAA),[3] is used to avoid aliasing (or "jaggies") on full-screen images.[4] SSAA was the first type of anti-aliasing available with early video cards. But due to its tremendous computational cost and with the advent of multisample anti-aliasing (MSAA) support on GPUs, it is no longer widely used in real time applications. MSAA provides somewhat lower graphic quality, but also tremendous savings in computational power.

The resulting image of SSAA may seem softer, and should also appear more realistic. However, while useful for photo-like images, a simple anti-aliasing approach (such as supersampling and then averaging) may actually worsen the appearance of some types of line art or diagrams (making the image appear fuzzy), especially where most lines are horizontal or vertical. In these cases, a prior grid-fitting step may be useful (see hinting).

In general, supersampling is a technique of collecting data points at a greater resolution (usually by a power of two) than the final data resolution. These data points are then combined (down-sampled) to the desired resolution, often just by a simple average. The combined data points have less visible aliasing artifacts (or moiré patterns).

Full-scene anti-aliasing by supersampling usually means that each full frame is rendered at double (2x) or quadruple (4x) the display resolution, and then down-sampled to match the display resolution. So a 2x FSAA would render 4 supersampled pixels for each single pixel of each frame. While rendering at larger resolutions will produce better results, more processor power is needed which can degrade performance and frame rate.

Sometimes FSAA is implemented in hardware in such a way that a graphical application is unaware the images are being supersampled and then down-sampled before being displayed.

Object-based anti-aliasing

A graphics rendering system creates an image based on objects constructed of polygonal primitives whereby the aliasing effects in the image are reduced by applying an anti-aliasing scheme only to the areas of the image representing silhouette edges of the objects. The silhouette edges are anti-aliased by creating anti-aliasing primitives which vary in opacity. These anti-aliasing primitives are joined to the silhouetted edges, and create a region in the image where the objects appear to blend into the background. The method has some important advantages over the classical methods based on the accumulation buffer since it generates full-scene anti-aliasing in only two passes and does not require the use of the additional memory required by the accumulation buffer. Object-based anti-aliasing was first developed at Silicon Graphics for their Indy workstation.

Anti-aliasing and gamma compression

Digital images are usually stored in a gamma-compressed format, but an optical anti-aliasing filter is linear. So to downsample an image in a way that would match optical blurring, one should first convert it to a linear format, then apply the anti-aliasing filter, and finally convert it back to a gamma compressed format. Computing anti-aliasing directly on the gamma-compressed image will lead to bright details (such as cat's whiskers) becoming visually thinner, and dark details (such as tree branches) becoming thicker, relative to the optically anti-aliased image. Almost all image editing software, including Adobe Photoshop and GIMP, process images in the gamma-compressed domain.

History

Important early works in the history of anti-aliasing include:

See also

References

  1. ^ Leler, William J. (July 1980). "Human Vision, Anti-aliasing, and the Cheap 4000 Line Display". ACM SIGGRAPH Computer Graphics 14 (3): 308–313. doi:10.1145/965105.807509. 
  2. ^ "AMD's Radeon HD 5870: Bringing About the Next Generation Of GPUs". AnandTech.com. http://www.anandtech.com/show/2841/14. 
  3. ^ Jason Gregory, Jeff Lander (2009). Game Engine Architecture. A K Peters, Ltd.. p. 39. ISBN 9781568814131. http://books.google.com/books?id=LJ20tsePKk4C&pg=PA442. 
  4. ^ M. Carmen Juan Lizandra (June 2000). "Graphic libraries for Windows programming". Crossroads, the ACM Student Magazine (ACM) 6 (4): 14–18. doi:10.1145/333424.333433. http://portal.acm.org/citation.cfm?id=333433. 

External links