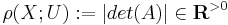Analytic torsion
In mathematics, Reidemeister torsion (or R-torsion, or Reidemeister–Franz torsion) is a topological invariant of manifolds introduced by Kurt Reidemeister (Reidemeister (1935)) for 3-manifolds and generalized to higher dimensions by Franz (1935) and de Rham (1936). Analytic torsion (or Ray–Singer torsion) is an invariant of Riemannian manifolds defined by Ray and Singer (1971, 1973a, 1973b) as an analytic analogue of Reidemeister torsion. Cheeger (1977, 1979) and Müller (1978) proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
Reidemeister torsion was the first invariant in algebraic topology that could distinguish between spaces which are homotopy equivalent but not homeomorphic, and can thus be seen as the birth of geometric topology as a distinct field. It can be used to classify lens spaces.
Reidemeister torsion is closely related to Whitehead torsion; see (Milnor 1966). For later work on torsion see the books (Turaev 2002), (Nicolaescu 2002, 2003).
Contents |
Definition of analytic torsion
If M is a Riemannian manifold and E a vector bundle over M, then there is a Laplacian operator acting on the i-forms with values in E. If the eigenvalues on i-forms are λj then the zeta function ζi is defined to be
for s large, and this is extended to all complex s by analytic continuation. The zeta regularized determinant of the Laplacian acting on i-forms is
which is formally the product of the positive eigenvalues of the laplacian acting on i-forms. The analytic torsion T(M,E) is defined to be
Definition of Reidemeister torsion
Let X be a finite connected CW-complex with fundamental group π := π1(X) and U an orthogonal finite-dimensional π-representation. Suppose that
for all n. If we fix a cellular basis for 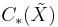 and an orthogonal R-basis for U, then
and an orthogonal R-basis for U, then ![D_*�:= U \otimes_{\mathbf{Z}[\pi]} C_*({\tilde X})](/2012-wikipedia_en_all_nopic_01_2012/I/17563f0a815d7e8b06a897db004af035.png) is a contractible finite based free R-chain complex. Let
is a contractible finite based free R-chain complex. Let 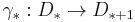 be any chain contraction of D*, i.e.
be any chain contraction of D*, i.e. 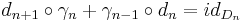 for all n. We obtain an isomorphism
for all n. We obtain an isomorphism 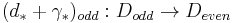 with
with  ,
,  . We define the Reidemeister torsion
. We define the Reidemeister torsion
where A is the matrix of (d* + γ*)odd with respect to the given bases. The Reidemeister torsion 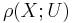 is independent of the choice of the cellular basis for
is independent of the choice of the cellular basis for 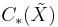 , the orthogonal basis for U and the chain contraction γ*.
, the orthogonal basis for U and the chain contraction γ*.
Examples
Reidemeister torsion was first used to classify 3-dimensional lens spaces in (Reidemeister 1935). The classification includes examples of homotopy equivalent 3-dimensional manifolds which are not homeomorphic – at the time (1935) the classification was only up to PL homeomorphism, but later (Brody 1960) showed that this was in fact a classification up to homeomorphism.
References
- Brody, E. J. (1960), "The topological classification of the lens spaces", Annals of Mathematics, 2 71 (1): 163–184, doi:10.2307/1969884, JSTOR 1969884
- Cheeger, Jeff (1977), "Analytic Torsion and Reidemeister Torsion", PNAS 74 (7): 2651–2654, doi:10.1073/pnas.74.7.2651, MR0451312, PMC 431228, PMID 16592411, http://www.pnas.org/cgi/content/abstract/74/7/2651
- Cheeger, Jeff (1979), "Analytic torsion and the heat equation", Ann. Of Math. (2) (Annals of Mathematics) 109 (2): 259–322, doi:10.2307/1971113, JSTOR 1971113, MR0528965
- Franz, W. (1935), "Ueber die Torsion einer Ueberdeckung", J. Reine Angew. Math. 173: 245–254
- Milnor, J. (1966), "Whitehead torsion.", Bull. Amer. Math. Soc. 72 (3): 358–426, doi:10.1090/S0002-9904-1966-11484-2, MR0196736, http://www.ams.org/bull/1966-72-03/S0002-9904-1966-11484-2/home.html
- Mishchenko, A.S. (2001), "Reidemeister torsion", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=R/r080960
- Müller, Werner (1978), "Analytic torsion and R-torsion of Riemannian manifolds.", Adv. In Math. 28 (3): 233–305, doi:10.1016/0001-8708(78)90116-0, MR0498252
- Nicolaescu, Liviu I. (2002), Notes on the Reidemeister torsion, http://www.nd.edu/~lnicolae/Torsion.pdf Online book
- Nicolaescu, Liviu I. (2003), The Reidemeister torsion of 3-manifolds, de Gruyter Studies in Mathematics, 30, Berlin: Walter de Gruyter & Co., pp. xiv+249, ISBN 3-11-017383-2, MR1968575
- Ray, D. B.; Singer, I. M. (1973a), "Analytic torsion for complex manifolds.", Ann. Of Math. (2) (Annals of Mathematics) 98 (1): 154–177, doi:10.2307/1970909, JSTOR 1970909, MR0383463
- Ray, D. B.; Singer, I. M. (1973b), "Analytic torsion.", Partial differential equations, Proc. Sympos. Pure Math., XXIII, Providence, R.I.: Amer. Math. Soc., pp. 167–181, MR0339293
- Ray, D. B.; Singer, I. M. (1971), "R-torsion and the Laplacian on Riemannian manifolds.", Advances in Math. 7 (2): 145–210, doi:10.1016/0001-8708(71)90045-4, MR0295381
- Reidemeister, Kurt (1935), "Homotopieringe und Linsenräume", Abh. Math. Sem. Univ. Hamburg 11: 102–109, doi:10.1007/BF02940717
- de Rham, G. (1936), "Sur les nouveaux invariants de M. Reidemeister", Mat. Sb. , 1 (5): 737–743
- Turaev, Vladimir (2002), Torsions of 3-dimensional manifolds, Progress in Mathematics, 208, Basel: Birkhäuser Verlag, pp. x+196, ISBN 3-7643-6911-6, MR1958479
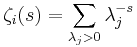
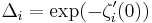
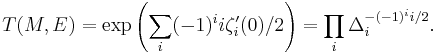
![H^\pi_n(X;U)�:= H_n(U \otimes_{\mathbf{Z}[\pi]} C_*({\tilde X})) = 0](/2012-wikipedia_en_all_nopic_01_2012/I/96feef345e4997e392853e0ebd2472e9.png)