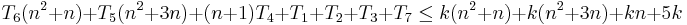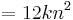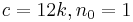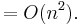Analysis of algorithms
In computer science, the analysis of algorithms is the determination of the amount of resources (such as time and storage) necessary to execute them. Most algorithms are designed to work with inputs of arbitrary length. Usually the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps (time complexity) or storage locations (space complexity).
Algorithm analysis is an important part of a broader computational complexity theory, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search for efficient algorithms.
In theoretical analysis of algorithms it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. Big O notation, omega notation and theta notation are used to this end. For instance, binary search is said to run in a number of steps proportional to the logarithm of the length of the list being searched, or in O(log(n)), colloquially "in logarithmic time". Usually asymptotic estimates are used because different implementations of the same algorithm may differ in efficiency. However the efficiencies of any two "reasonable" implementations of a given algorithm are related by a constant multiplicative factor called a hidden constant.
Exact (not asymptotic) measures of efficiency can sometimes be computed but they usually require certain assumptions concerning the particular implementation of the algorithm, called model of computation. A model of computation may be defined in terms of an abstract computer, e.g., Turing machine, and/or by postulating that certain operations are executed in unit time. For example, if the sorted list to which we apply binary search has n elements, and we can guarantee that each lookup of an element in the list can be done in unit time, then at most log2 n + 1 time units are needed to return an answer.
Contents |
Cost models
Time efficiency estimates depend on what we define to be a step. For the analysis to correspond usefully to the actual execution time, the time required to perform a step must be guaranteed to be bounded above by a constant. One must be careful here; for instance, some analyses count an addition of two numbers as one step. This assumption may not be warranted in certain contexts. For example, if the numbers involved in a computation may be arbitrarily large, the time required by a single addition can no longer be assumed to be constant.
Two cost models are generally used:[1][2][3][4][5]
- the uniform cost model, also called uniform-cost measurement (and similar variations), assigns a constant cost to every machine operation, regardless of the size of the numbers involved
- the logarithmic cost model, also called logarithmic-cost measurement (and variations thereof), assigns a cost to every machine operation proportional to the number of bits involved
The latter is more cumbersome to use, so it's only employed when necessary, for example in the analysis of arbitrary-precision arithmetic algorithms, like those used in cryptography.
A key point which is often overlooked is that published lower bounds for problems are often given for a model of computation that is more restricted than the set of operations that you could use in practice and therefore there are algorithms that are faster than what would naively be thought possible.[6]
Run-time analysis
Run-time analysis is a theoretical classification that estimates and anticipates the increase in running time (or run-time) of an algorithm as its input size (usually denoted as n) increases. Run-time efficiency is a topic of great interest in computer science: A program can take seconds, hours or even years to finish executing, depending on which algorithm it implements (see also performance analysis, which is the analysis of an algorithm's run-time in practice).
Shortcomings of empirical metrics
Since algorithms are platform-independent (i.e. a given algorithm can be implemented in an arbitrary programming language on an arbitrary computer running an arbitrary operating system), there are significant drawbacks to using an empirical approach to gauge the comparative performance of a given set of algorithms.
Take as an example a program that looks up a specific entry in a sorted list of size n. Suppose this program were implemented on Computer A, a state-of-the-art machine, using a linear search algorithm, and on Computer B, a much slower machine, using a binary search algorithm. Benchmark testing on the two computers running their respective programs might look something like the following:
| n (list size) | Computer A run-time (in nanoseconds) |
Computer B run-time (in nanoseconds) |
|---|---|---|
| 15 | 7 | 100,000 |
| 65 | 32 | 150,000 |
| 250 | 125 | 200,000 |
| 1,000 | 500 | 250,000 |
Based on these metrics, it would be easy to jump to the conclusion that Computer A is running an algorithm that is far superior in efficiency to that of Computer B. However, if the size of the input-list is increased to a sufficient number, that conclusion is dramatically demonstrated to be in error:
| n (list size) | Computer A run-time (in nanoseconds) |
Computer B run-time (in nanoseconds) |
|---|---|---|
| 15 | 7 | 100,000 |
| 65 | 32 | 150,000 |
| 250 | 125 | 200,000 |
| 1,000 | 500 | 250,000 |
| ... | ... | ... |
| 1,000,000 | 500,000 | 500,000 |
| 4,000,000 | 2,000,000 | 550,000 |
| 16,000,000 | 8,000,000 | 600,000 |
| ... | ... | ... |
| 63,072 × 1012 | 31,536 × 1012 ns, or 1 year |
1,375,000 ns, or 1.375 milliseconds |
Computer A, running the linear search program, exhibits a linear growth rate. The program's run-time is directly proportional to its input size. Doubling the input size doubles the run time, quadrupling the input size quadruples the run-time, and so forth. On the other hand, Computer B, running the binary search program, exhibits a logarithmic growth rate. Doubling the input size only increases the run time by a constant amount (in this example, 25,000 ns). Even though Computer A is ostensibly a faster machine, Computer B will inevitably surpass Computer A in run-time because it's running an algorithm with a much slower growth rate.
Orders of growth
Informally, an algorithm can be said to exhibit a growth rate on the order of a mathematical function if beyond a certain input size n, the function f(n) times a positive constant provides an upper bound or limit for the run-time of that algorithm. In other words, for a given input size n greater than some n0 and a constant c, the running time of that algorithm will never be larger than c × f(n). This concept is frequently expressed using Big O notation. For example, since the run-time of insertion sort grows quadratically as its input size increases, insertion sort can be said to be of order O(n²).
Big O notation is a convenient way to express the worst-case scenario for a given algorithm, although it can also be used to express the average-case — for example, the worst-case scenario for quicksort is O(n²), but the average-case run-time is O(n log n).[7]
Empirical orders of growth
Assuming the order of growth follows power rule, 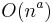 , the coefficient a can be found by taking empirical measurements (of run time, say),
, the coefficient a can be found by taking empirical measurements (of run time, say), 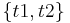 at some problem-size points
at some problem-size points 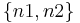 , and calculating
, and calculating 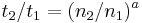 so that
so that 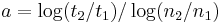 . If the order of growth indeed follows the power rule, the empirical value of a will stay constant at different ranges, and if not, it will change - but still could serve for comparison of any two given algorithms as to their empirical local orders of growth behaviour. Applied to the above table:
. If the order of growth indeed follows the power rule, the empirical value of a will stay constant at different ranges, and if not, it will change - but still could serve for comparison of any two given algorithms as to their empirical local orders of growth behaviour. Applied to the above table:
| n (list size) | Computer A run-time (in nanoseconds) |
Local order of growth (n^_) |
Computer B run-time (in nanoseconds) |
Local order of growth (n^_) |
|---|---|---|---|---|
| 15 | 7 | 100,000 | ||
| 65 | 32 | 1.04 | 150,000 | 0.28 |
| 250 | 125 | 1.01 | 200,000 | 0.21 |
| 1,000 | 500 | 1.00 | 250,000 | 0.16 |
| ... | ... | ... | ... | ... |
| 1,000,000 | 500,000 | 500,000 | ||
| 4,000,000 | 2,000,000 | 1.00 | 550,000 | 0.07 |
| 16,000,000 | 8,000,000 | 1.00 | 600,000 | 0.06 |
| ... | ... | ... | ... | ... |
It is clearly seen that the first algorithm exhibits a linear order of growth indeed following the power rule. The empirical values for the second one are diminishing rapidly, suggesting it follows another rule of growth and in any case has much lower local order of growth (and improving further still), empirically, than the first one.
Evaluating run-time complexity
The run-time complexity for the worst-case scenario of a given algorithm can sometimes be evaluated by examining the structure of the algorithm and making some simplifying assumptions. Consider the following pseudocode:
1 get a positive integer from input 2 if n > 10 3 print "This might take a while..." 4 for i = 1 to n 5 for j = 1 to i 6 print i * j 7 print "Done!"
A given computer will take a discrete amount of time to execute each of the instructions involved with carrying out this algorithm. The specific amount of time to carry out a given instruction will vary depending on which instruction is being executed and which computer is executing it, but on a conventional computer, this amount will be deterministic.[8] Say that the actions carried out in step 1 are considered to consume time T1, step 2 uses time T2, and so forth.
In the algorithm above, steps 1, 2 and 7 will only be run once. For a worst-case evaluation, it should be assumed that step 3 will be run as well. Thus the total amount of time to run steps 1-3 and step 7 is:
The loops in steps 4, 5 and 6 are trickier to evaluate. The outer loop test in step 4 will execute ( n + 1 ) times (note that an extra step is required to terminate the for loop, hence n + 1 and not n executions), which will consume T4( n + 1 ) time. The inner loop, on the other hand, is governed by the value of i, which iterates from 1 to n. On the first pass through the outer loop, j iterates from 1 to 1: The inner loop makes one pass, so running the inner loop body (step 6) consumes T6 time, and the inner loop test (step 5) consumes 2T5 time. During the next pass through the outer loop, j iterates from 1 to 2: the inner loop makes two passes, so running the inner loop body (step 6) consumes 2T6 time, and the inner loop test (step 5) consumes 3T5 time.
Altogether, the total time required to run the inner loop body can be expressed as an arithmetic progression:
The total time required to run the inner loop test can be evaluated similarly:
which can be factored as
Therefore the total running time for this algorithm is:
which reduces to
As a rule-of-thumb, one can assume that the highest-order term in any given function dominates its rate of growth and thus defines its run-time order. In this example, n² is the highest-order term, so one can conclude that f(n) = O(n²). Formally this can be proven as follows:
Prove that
(for n ≥ 0)
Let k be a constant greater than or equal to [T1..T7]
(for n ≥ 1)
Thereforefor
A more elegant approach to analyzing this algorithm would be to declare that [T1..T7] are all equal to one unit of time greater than or equal to [T1..T7]. This would mean that the algorithm's running time breaks down as follows:[10]
(for n ≥ 1)
Growth rate analysis of other resources
The methodology of run-time analysis can also be utilized for predicting other growth rates, such as consumption of memory space. As an example, consider the following pseudocode which manages and reallocates memory usage by a program based on the size of a file which that program manages:
while (file still open)
let n = size of file
for every 100,000 kilobytes of increase in file size
double the amount of memory reserved
In this instance, as the file size n increases, memory will be consumed at an exponential growth rate, which is order O(2n).[11]
Relevance
Algorithm analysis is important in practice because the accidental or unintentional use of an inefficient algorithm can significantly impact system performance. In time-sensitive applications, an algorithm taking too long to run can render its results outdated or useless. An inefficient algorithm can also end up requiring an uneconomical amount of computing power or storage in order to run, again rendering it practically useless.
See also
- Amortized analysis
- Asymptotic analysis
- Asymptotic computational complexity
- Best, worst and average case
- Big O notation
- Computational complexity theory
- Master theorem
- NP-Complete
- Numerical analysis
- Polynomial time
- Program optimization
- Profiling (computer programming)
- Smoothed analysis
- Time complexity — includes table of orders of growth for common algorithms
Notes
- ^ Alfred V. Aho; John E. Hopcroft; Jeffrey D. Ullman (1974). The design and analysis of computer algorithms. Addison-Wesley Pub. Co.., section 1.3
- ^ Juraj Hromkovič (2004). Theoretical computer science: introduction to Automata, computability, complexity, algorithmics, randomization, communication, and cryptography. Springer. pp. 177–178. ISBN 9783540140153. http://books.google.com/books?id=KpNet-n262QC&pg=PA177.
- ^ Giorgio Ausiello (1999). Complexity and approximation: combinatorial optimization problems and their approximability properties. Springer. pp. 3–8. ISBN 9783540654315. http://books.google.com/books?id=Yxxw90d9AuMC&pg=PA3.
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, p. 20, ISBN 978-3-540-21045-0, http://books.google.com/books?id=u7DZSDSUYlQC&pg=PA20
- ^ Robert Endre Tarjan (1983). Data structures and network algorithms. SIAM. pp. 3–7. ISBN 9780898711875. http://books.google.com/books?id=JiC7mIqg-X4C&pg=PA3.
- ^ Examples of the price of abstraction?, cstheory.stackexchange.com
- ^ The term lg is often used as shorthand for log2
- ^ However, this is not the case with a quantum computer
- ^ It can be proven by induction that
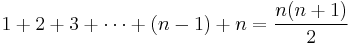
- ^ This approach, unlike the above approach, neglects the constant time consumed by the loop tests which terminate their respective loops, but it is trivial to prove that such omission does not affect the final result
- ^ Note that this is an extremely rapid and most likely unmanageable growth rate for consumption of memory resources
References
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001). Introduction to Algorithms. Chapter 1: Foundations (Second ed.). Cambridge, MA: MIT Press and McGraw-Hill. pp. 3–122. ISBN 0262032937.
- Sedgewick, Robert (1998). Algorithms in C, Parts 1-4: Fundamentals, Data Structures, Sorting, Searching (3rd ed.). Reading, MA: Addison-Wesley Professional. ISBN 9780201314526.
- Knuth, Donald. The Art of Computer Programming. Addison-Wesley.
- Greene, Daniel A.; Knuth, Donald E. (1982). Mathematics for the Analysis of Algorithms (Second ed.). Birkhäuser. ISBN 374633102X.
- Goldreich, Oded (2008). Computational Complexity: A Conceptual Perspective. Cambridge University Press. ISBN 9780521884730.
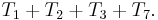

![T_6 \left[ 1 %2B 2 %2B 3 %2B \cdots %2B (n-1) %2B n \right] = T_6 \left[ \frac{1}{2} (n^2 %2B n) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/8de5435b963f5e8c52dbc7ed5b64c9c1.png)
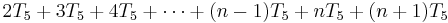
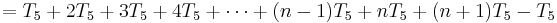
![T_5 \left[ 1%2B2%2B3%2B\cdots %2B (n-1) %2B n %2B (n %2B 1) \right] - T_5 = T_5 \left[ \frac{1}{2} (n^2 %2B 3n %2B 2) \right] - T_5](/2012-wikipedia_en_all_nopic_01_2012/I/0101a260f80ecaff4bbf39e009931c02.png)
![f(n) = T_1 %2B T_2 %2B T_3 %2B T_7 %2B (n %2B 1)T_4 %2B \left[ \frac{1}{2} (n^2 %2B n) \right] T_6 %2B \left[ \frac{1}{2} (n^2%2B3n%2B2) \right] T_5 - T_5](/2012-wikipedia_en_all_nopic_01_2012/I/4aec8902816b11e711564bfa29d7e867.png)
![f(n) = \left[ \frac{1}{2} (n^2 %2B n) \right] T_6 %2B \left[ \frac{1}{2} (n^2 %2B 3n) \right] T_5 %2B (n %2B 1)T_4 %2B T_1 %2B T_2 %2B T_3 %2B T_7](/2012-wikipedia_en_all_nopic_01_2012/I/df2f15fe0874e097492086095739fbf6.png)
![\left[ \frac{1}{2} (n^2 %2B n) \right] T_6 %2B \left[ \frac{1}{2} (n^2 %2B 3n) \right] T_5 %2B (n %2B 1)T_4 %2B T_1 %2B T_2 %2B T_3 %2B T_7 \le cn^2,\ n \ge n_0](/2012-wikipedia_en_all_nopic_01_2012/I/39894c6021930d5ed7bb0eeff96867d7.png)
![\left[ \frac{1}{2} (n^2 %2B n) \right] T_6 %2B \left[ \frac{1}{2} (n^2 %2B 3n) \right] T_5 %2B (n %2B 1)T_4 %2B T_1 %2B T_2 %2B T_3 %2B T_7](/2012-wikipedia_en_all_nopic_01_2012/I/2377e74c419d1fa5b5dd4c81f5c0ee02.png)