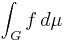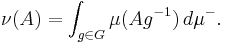Amenable group
In mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements. The original definition, in terms of a finitely additive invariant measure (or mean) on subsets of G, was introduced by John von Neumann in 1929 under the German name "messbar" ("measurable" in English) in response to the Banach–Tarski paradox. In 1949 Mahlon M. Day introduced the English translation "amenable", apparently as a pun.[1]
The amenability property has a large number of equivalent formulations. In the field of analysis, the definition is in terms of linear functionals. An intuitive way to understand this version is that the support of the regular representation is the whole space of irreducible representations.
In discrete group theory, where G has no topological structure, a simpler definition is used. In this setting, a group is amenable if one can say what percentage of G any given subset takes up.
If a group has a Følner sequence then it is automatically amenable.
Contents |
Locally compact definition
Let  be a locally compact hausdorff group. Then it is well-known that it possesses a unique, up-to-scale left- (or right-) rotation invariant ring (borel regular in the case of
be a locally compact hausdorff group. Then it is well-known that it possesses a unique, up-to-scale left- (or right-) rotation invariant ring (borel regular in the case of  second countable) measure (left and right probability measure in the case of
second countable) measure (left and right probability measure in the case of  compact), the Haar measure. Consider the banach space
compact), the Haar measure. Consider the banach space 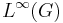 of essentially-bounded measurable functions within this measure space (which is clearly independent of the scale of the Haar measure).
of essentially-bounded measurable functions within this measure space (which is clearly independent of the scale of the Haar measure).
Definition 1. An operator 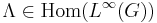 is said to be a mean if
is said to be a mean if 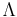 has norm 1 and is non-negative (i.e.
has norm 1 and is non-negative (i.e. 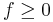 a.e. implies
a.e. implies 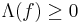 ).
).
Definition 2. A mean 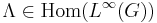 is said to be a left-invariant (resp. right-invariant) if
is said to be a left-invariant (resp. right-invariant) if 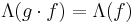 all
all 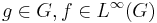 with respect to the left (resp. right) shift action of
with respect to the left (resp. right) shift action of 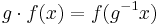 (resp.
(resp. 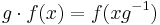 ).
).
Definition 3. A locally compact hausdorff group is called amenable if it admits a left- (or right-)invariant mean.
Discrete definition
The definition of amenability is quite a lot simpler in the case of a discrete group, i.e. a group with no topological structure.
Definition. A discrete group G is amenable if there is a finitely additive measure (also called a mean) —a function that assigns to each subset of G a number from 0 to 1—such that
- The measure is a probability measure: the measure of the whole group G is 1.
- The measure is finitely additive: given finitely many disjoint subsets of G, the measure of the union of the sets is the sum of the measures.
- The measure is left-invariant: given a subset A and an element g of G, the measure of A equals the measure of gA. (gA denotes the set of elements ga for each element a in A. That is, each element of A is translated on the left by g.)
This definition can be summarized thus:G is amenable if it has a finitely-additive left-invariant probability measure. Given a subset A of G, the measure can be thought of as answering the question: what is the probability that a random element of G is in A?
It is a fact that this definition is equivalent to the definition in terms of L∞(G).
Having a measure  on G allows us to define integration of bounded functions on G. Given a bounded function
on G allows us to define integration of bounded functions on G. Given a bounded function 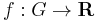 , the integral
, the integral
is defined as in Lebesgue integration. (Note that some of the properties of the Lebesgue integral fail here, since our measure is only finitely additive.)
If a group has a left-invariant measure, it automatically has a bi-invariant one. Given a left-invariant measure  , the function
, the function 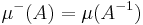 is a right-invariant measure. Combining these two gives a bi-invariant measure:
is a right-invariant measure. Combining these two gives a bi-invariant measure:
Conditions for a discrete group
The following conditions are equivalent for a countable discrete group Γ:
- Γ is amenable.
- If Γ acts by isometries on a (separable) Banach space E, leaving a weakly closed convex subset C of the closed unit ball of E* invariant, then Γ has a fixed point in C.
- There is a left invariant norm-continuous functional μ on l∞(Γ) with μ(1) = 1 (this requires the axiom of choice).
- There is a left invariant state μ on any left invariant separable unital C* subalgebra of l∞(Γ).
- There is a set of probability measures μn on Γ such that ||g · μn − μn||1 tends to 0 for each g in Γ (M.M. Day).
- There are unit vectors xn in l2(Γ) such that ||g · xn − xn||2 tends to 0 for each g in Γ (J. Dixmier).
- There are finite subsets Sn of Γ such that | g · Sn Δ Sn | / |Sn| tends to 0 for each g in Γ (Følner).
- If μ is a symmetric probability measure on Γ with support generating Γ, then convolution by μ defines an operator of norm 1 on l2(Γ) (Kesten).
- If Γ acts by isometries on a (separable) Banach space E and f in l∞(Γ, E*) is a bounded 1-cocycle, i.e. f(gh) = f(g) + g·f(h), then f is a 1-coboundary, i.e. f(g) = g·φ − φ for some φ in E* (B.E. Johnson).
- The von Neumann group algebra of Γ is hyperfinite (A. Connes).
Examples
- Finite groups are amenable. Use the counting measure with the discrete definition.
- Subgroups of amenable groups are amenable.
- The direct product of two amenable groups is amenable, while the direct product of an infinite family of amenable groups need not be.
- The group of integers is amenable (a sequence of intervals of length tending to infinity is a Følner sequence).The existence of a shift-invariant, finitely additive probability measure on the group Z also follows easily from the Hahn-Banach theorem this way. Let S be the shift operator on the sequence space ℓ∞(Z), which is defined by (Sx)i = xi+1 for all x ∈ ℓ∞(Z), and let u ∈ ℓ∞(Z) be the constant sequence ui =1 for all i ∈ Z. Any element y ∈ Y:=Ran(S-I) has a distance larger than or equal to 1 from u (otherwise yi = xi+1 - xi would be positive and bounded away from zero, whence xi could not be bounded). This implies that there is a well-defined norm-one linear form on the subspace Ru + Y taking tu + y to t. By the Hahn-Banach theorem the latter admits a norm-one linear extension on ℓ∞(Z), which is by construction a shift-invariant finitely additive probability measure on Z.
- A group is amenable if all its finitely generated subgroups are. That is, locally amenable groups are amenable.
- By the fundamental theorem of finitely generated abelian groups, it follows that abelian groups are amenable.
- A group is amenable if it has an amenable normal subgroup such that the quotient is amenable. That is, extensions of amenable groups by amenable groups are amenable.
- It follows that a group is amenable if it has a finite index amenable subgroup. That is, virtually amenable groups are amenable.
- Furthermore, it follows that all solvable groups are amenable.
- Compact groups are amenable. The Haar measure is an invariant mean (unique taking total measure 1).
- Finitely generated groups of subexponential growth are amenable.
Non-examples
If a countable discrete group contains a (non-abelian) free subgroup on two generators, then it is not amenable. The converse to this statement is the so-called von Neumann conjecture, which was disproved by Olshanskii in 1980 using his Tarski monsters. Adyan subsequently showed that free Burnside groups are non-amenable: since they are periodic, they cannot contain the free group on two generators. These groups are finitely generated, but not finitely presented. However, in 2002 Sapir and Olshanskii found finitely presented counterexamples: non-amenable finitely presented groups that have a periodic normal subgroup with quotient the integers.[2]
For finitely generated linear groups, however, the von Neumann conjecture is true by the Tits alternative[3]: every subgroup of GL(n,k) with k a field either has a normal solvable subgroup of finite index (and therefore is amenable) or contains the free group on two generators. Although Tits' proof used algebraic geometry, Guivarc'h later found an analytic proof based on V. Oseledets' multiplicative ergodic theorem.[4] Analogues of the Tits alternative have been proved for many other classes of groups, such as fundamental groups of 2-dimensional simplicial complexes of non-positive curvature.[5]
See also
Notes
- ^ Day's first published use of the word is in his abstract for an AMS summer meeting in 1949, Means on semigroups and groups, Bull. A.M.S. 55 (1949) 1054–1055. Many text books on amenabilty, such as Volker Runde's, suggest that Day chose the word as a pun.
- ^ Olshanskii, Alexander Yu.; Sapir, Mark V. (2002), "Non-amenable finitely presented torsion-by-cyclic groups", Publ. Math. Inst. Hautes Études Sci. 96: 43–169
- ^ Tits, J. (1972), "Free subgroups in linear groups", J. Algebra 20 (2): 250–270, doi:10.1016/0021-8693(72)90058-0
- ^ Guivarc'h, Yves (1990), "Produits de matrices aléatoires et applications aux propriétés géometriques des sous-groupes du groupes linéaire", Ergod. Th. & Dynam. Sys. 10 (3): 483–512, doi:10.1017/S0143385700005708
- ^ Ballmann, Werner; Brin, Michael (1995), "Orbihedra of nonpositive curvature", Inst. Hautes Études Sci. Publ. Math. 82: 169–209, doi:10.1007/BF02698640
References
- F.P. Greenleaf, Invariant Means on Topological Groups and Their Applications, Van Nostrand Reinhold (1969).
- V. Runde, Lectures on Amenability, Lecture Notes in Mathematics 1774, Springer (2002).
- M. Takesaki, Theory of Operator Algebras, Vol. 2 and 3, Springer.
- J. von Neumann, Zur allgemeinen Theorie des Maßes, Fund. Math. 13 (1929), 73−111. JFM 55.0151.01
- This article incorporates material from Amenable group on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.