Almost integer
In recreational mathematics an almost integer is any number that is very close to an integer. Well known examples of almost integers are high powers of the golden ratio 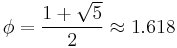 , for example:
, for example:
The fact that these powers approach integers is non-coincidental, which is trivially seen because the golden ratio is a Pisot-Vijayaraghavan number.
Other occurrences of non-coincidental near-integers involve the three largest Heegner numbers:
where the non-coincidence can be better appreciated when expressed in the common simple form[2]:
where :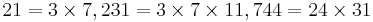 and the reason for the squares being due to certain Eisenstein series. The constant
and the reason for the squares being due to certain Eisenstein series. The constant 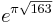 is sometimes referred to as Ramanujan's constant.
is sometimes referred to as Ramanujan's constant.
Almost integers involving the mathematical constants pi and e have often puzzled mathematicians. An example is
To date, no explanation has been given for why Gelfond's constant ( 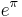 ) is nearly identical to
) is nearly identical to 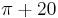 ,[1] which is therefore regarded to be a mathematical coincidence.
,[1] which is therefore regarded to be a mathematical coincidence.
Another example is
Also consider π in cubic expressions
or
where the second one is obvious from the first one.
Also consider π in quadratic expressions
or
where the second one is obvious from the first one.
Here are more examples:
another interesting example can be define as the lagerst root of 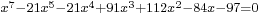 ,approximate
,approximate 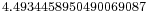 and the first positive root of
and the first positive root of 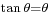 ,approximate
,approximate 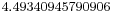 . What is more,however,the septic is solvable,
. What is more,however,the septic is solvable,
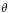 can also be express in terms of elementary integrals:
can also be express in terms of elementary integrals:
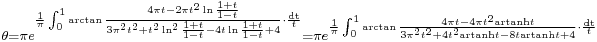
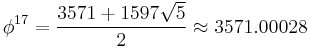
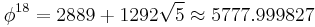
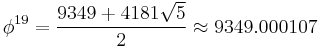
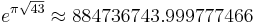
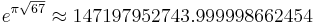
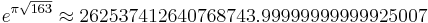
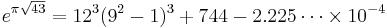
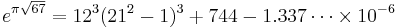
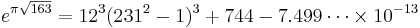
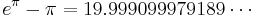
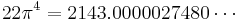
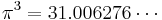
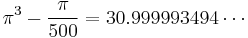
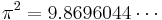
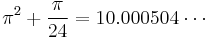
![{}_{\cos\left\{\pi\cos\left[\pi\cos\ln\left(\pi%2B20\right)\right]\right\}\approx -0.9999999999999999999999999999999999606783 }](/2012-wikipedia_en_all_nopic_01_2012/I/6b8b960a2a2a4d2ee654166a71151490.png)
![{}_{\sin2017\sqrt[5]2\approx -0.9999999999999999785}](/2012-wikipedia_en_all_nopic_01_2012/I/dbe11a220bb5ebd7b88b12ad45e1687f.png)
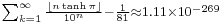
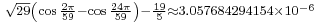
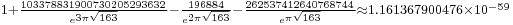
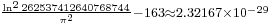
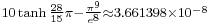
![{}_{ \sqrt[4]{\frac{91}{10}}-\frac{33}{19}\approx 3.661398\times10^{-8}}](/2012-wikipedia_en_all_nopic_01_2012/I/94265f5a5138c4479b45dd93cef528cd.png)
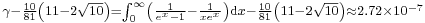
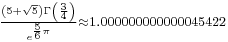
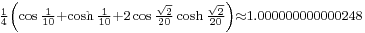
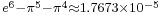
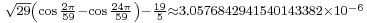
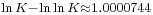
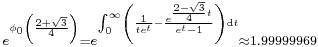
![{}_{ \frac{\sqrt[3]9}{3\ln 2}\approx 1.00030887}](/2012-wikipedia_en_all_nopic_01_2012/I/6e3df55c6794a4ef37132df88d898286.png)
![{}_{\sum_{k=-\infty}^{\infty}10^{-\frac{k^2}{10000}}-100\sqrt{\frac{\pi}{\ln10}}=\theta_3\left(0,\frac{1}{\sqrt[10000]{10}}\right)-100\sqrt{\frac{\pi}{\ln10}}\approx1.3809\times10^{-18613}}](/2012-wikipedia_en_all_nopic_01_2012/I/23634e85bfad95ecd8b348ed807bed6d.png)
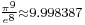
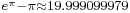
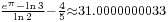
![{}_{\frac{\pi^{11}}{e^3}-\Gamma\left[\Gamma\left(\pi%2B1\right)%2B1\right]=\frac{\pi^{11}}{e^3}-\int_0^{\infty}\frac{t^{\int_0^{\infty}\frac{u^{\pi}}{e^u}{\rm{d}}u}}{e^t} {\rm{d}}t\approx 7266.9999993632596}](/2012-wikipedia_en_all_nopic_01_2012/I/316613fc750bbef9193db02090f976b8.png)
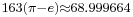
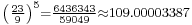
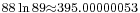
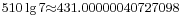
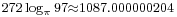
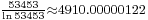
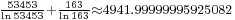
![{}_{\sqrt[8]{\frac{\sqrt2}{4}\left(\pi^{17}-4e^{2\pi}%2B4\pi e^{\pi}\right)}-\sqrt[8]{\frac{\sqrt2}{4}\left(\pi^{17}-4e^{2\pi}-4\pi e^{\pi}\right)}\approx 2.570287024592328869357\times 10^{-6}}](/2012-wikipedia_en_all_nopic_01_2012/I/c67ad7ba41342ead94a3be6535312f5c.png)
![{}_{10-\sqrt[8]{\frac{\sqrt2}{4}\left(\pi^{17}-4e^{2\pi}-4\pi e^{\pi}\right)}\approx 2.57055302118\times 10^{-6}}](/2012-wikipedia_en_all_nopic_01_2012/I/5ced6d92b40b9ac62c504ef29c89bed8.png)
![{}_{10-\sqrt[8]{\frac{\sqrt2}{4}\left(\pi^{17}-4e^{2\pi}%2B4\pi e^{\pi}\right)}\approx 2.65996596963\times 10^{-10}}](/2012-wikipedia_en_all_nopic_01_2012/I/3061a1ce49870fdc1ddf708badabfecf.png)
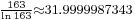
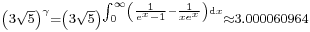
![{}_{\frac{10}{81}-\sum_{n=1}^\infty\frac{\sum_{k=10^{n-1}}^{10^n-1}10^{-n\left[k-(10^{n-1}-1)\right]}k}{10^{\sum_{k=0}^{n-1}9\times 10^{k-1}k}}=\frac{10}{81}-\sum_{n=1}^\infty\sum_{k=10^{n-1}}^{10^n-1}\frac{k}{10^{kn-9\sum_{k=0}^{n-1}10^k(n-k)}}\approx 1.022344\times10^{-9}}](/2012-wikipedia_en_all_nopic_01_2012/I/5b2be679b65a4b5e46ebadd09c34b39b.png)
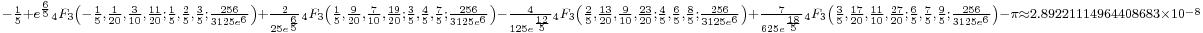
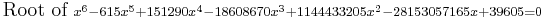
![{}_{\frac{615-55\sqrt5-\sqrt[3]{7451370%2B3332354\sqrt5%2B6\sqrt{8890710030%2B3976046490\sqrt5}}-\sqrt[3]{7451370%2B3332354\sqrt5-6\sqrt{8890710030%2B3976046490\sqrt5}}}{6}\approx 1.40677447684\times10^{-6}}](/2012-wikipedia_en_all_nopic_01_2012/I/5c3c73e7f2ce2c08a1b39484ba1fbe97.png)
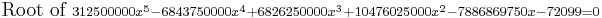
![{}_{\tan\left(\frac{\arctan 4}{5}%2B\frac{4\pi}{5}\right)%2B\frac{19}{50}=\frac{219}{50}%2B\frac{-1-\sqrt5%2B\sqrt{10-2\sqrt5}{\rm{i}}}{4}\sqrt[5]{884%2B799{\rm{i}}}%2B\frac{-1-\sqrt5-\sqrt{10-2\sqrt5}{\rm{i}}}{4}\sqrt[5]{884-799{\rm{i}}}%2B\frac{-1%2B\sqrt5-\sqrt{10%2B2\sqrt5}{\rm{i}}}{4}\sqrt[5]{1156%2B289{\rm{i}}}%2B\frac{-1%2B\sqrt5%2B\sqrt{10%2B2\sqrt5}{\rm{i}}}{4}\sqrt[5]{1156-289{\rm{i}}}\approx -9.141538637378949398666277\times 10^{-6}}](/2012-wikipedia_en_all_nopic_01_2012/I/53efd82ce51bd8ec2c6f4c2f39a855fd.png)
![{}_{\rm{erfi}\left(\rm{erfi}\frac{\sqrt3}{3}\right)=\frac{2}{\sqrt\pi}\int_0^{\frac{2}{\sqrt\pi}\int_0^{\frac{\sqrt3}{3}} e^{t^2} \rm{d} t} e^{u^2} \rm{d} u
=\frac{2}{\sqrt\pi}e^{\left(\frac{2\sqrt[3]e}{\sqrt\pi}\int_0^{\infty}\frac{\sin\left(\frac{2}{3}\sqrt3t\right)}{e^{t^2}}{\rm{d}}t\right)^2}\int_0^{\infty}\frac{\sin\left[\frac{4u\sqrt[3]e}{\sqrt\pi}\int_0^{\infty}\frac{\sin\left(\frac{2}{3}\sqrt3t\right)}{e^{t^2}}{\rm{d}}t\right]}{e^{u^2}}{\rm{d}}u
=\frac{2}{\sqrt\pi}\int_0^{{}_{\frac{2\sqrt[3]e}{\sqrt\pi}\int_0^{\infty}\frac{\sin\left(\frac{2}{3}\sqrt3t\right)}{e^{t^2}}{\rm{d}}t}} e^{u^2} {\rm{d}} u
=\frac{2}{\sqrt\pi}e^{\left(\frac{2}{\sqrt\pi}\int_0^{\frac{\sqrt3}{3}} e^{t^2} \rm{d} t\right)^2}\int_0^{\infty}\frac{\sin\left(\frac{4u}{\sqrt\pi}\int_0^{\frac{\sqrt3}{3}} e^{t^2} \rm{d} t\right)}{e^{u^2}} {\rm{d}} u\approx 1.00002087363809430195879}](/2012-wikipedia_en_all_nopic_01_2012/I/42c227ad28879f82a4c71740d29b1119.png)
![{}_{K=2e^{\frac{1}{\ln 2}\int_0^1\frac{1}{x^2%2Bx}\ln \frac{\pi\left(x-x^3\right)}{\sin\left(\pi x\right)}{\rm{d}} x}=2e^{\frac{1}{\ln 2}\int_0^1\frac{1}{x^2%2Bx}\ln \left[\Gamma\left(2-x\right)\right]\ln \left[\Gamma\left(2%2Bx\right)\right]{\rm{d}} x}=\sqrt2e^{\frac{\pi^2}{12\ln 2}%2B\frac{1}{\ln 2}\int_0^{\pi}\frac{\ln\left(\theta|\cot\theta|\right)}{\theta}{\rm{d}} \theta}}](/2012-wikipedia_en_all_nopic_01_2012/I/e426107cdea29273ed9ccc0eecc3478f.png)
![{}_{{}_{\frac{\sqrt[7]{23328}}{6}\left\{\left[-\frac{1}{6}%2B\frac{\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\sqrt[3]{28-84\sqrt3{\rm{i}}}}{12}%2B {\rm{i}} \left(-\frac{\sqrt7}{6}%2B\frac{-1-\sqrt3{\rm{i}}}{24}\sqrt[3]{52\sqrt7%2B12\sqrt{21}{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{24}\sqrt[3]{52\sqrt7-12\sqrt{21}{\rm{i}}}\right)\right]
\sqrt[7]{-2%2B\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\sqrt[3]{28-84\sqrt3{\rm{i}}}%2B\frac{\sqrt7}{7}\left(-14%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{2548%2B588\sqrt3{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{2548-588\sqrt3{\rm{i}}}\right){\rm{i}}}%2B
\left[ -\frac{1}{6}%2B\frac{\sqrt[3]{28%2B84\sqrt{3}{\rm{i}}}%2B\sqrt[3]{28-84\sqrt{3}{\rm{i}}}}{12}%2B{\rm{i}}\left(\frac{\sqrt7}{6}%2B\frac{-1-\sqrt3{\rm{i}}}{24}\sqrt[3]{-52\sqrt7%2B12\sqrt{21}{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{24}\sqrt[3]{-52\sqrt7-12\sqrt{21}{\rm{i}}}\right)\right]
\sqrt[7]{-2%2B\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\sqrt[3]{28-84\sqrt3{\rm{i}}}%2B\frac{\sqrt7}{7}\left(14%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{-2548%2B588\sqrt3{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{-2548-588\sqrt3{\rm{i}}}\right){\rm{i}}}%2B
\left[ -\frac{1}{6}%2B\frac{\sqrt[3]{28%2B84\sqrt{3}{\rm{i}}}%2B\sqrt[3]{28-84\sqrt{3}{\rm{i}}}}{12}%2B{\rm{i}}\left(\frac{\sqrt7}{6}%2B\frac{-1-\sqrt3{\rm{i}}}{24}\sqrt[3]{-52\sqrt7%2B12\sqrt{21}{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{24}\sqrt[3]{-52\sqrt7-12\sqrt{21}{\rm{i}}}\right)\right]
\sqrt[7]{-2%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{28-84\sqrt3{\rm{i}}}%2B\frac{\sqrt7}{7}\left(-14%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{2548%2B588\sqrt3{\rm{i}}}%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{2548-588\sqrt3{\rm{i}}}\right){\rm{i}}}%2B
\left[ -\frac{1}{6}%2B\frac{\sqrt[3]{28%2B84\sqrt{3}{\rm{i}}}%2B\sqrt[3]{28-84\sqrt{3}{\rm{i}}}}{12}%2B {\rm{i}} \left(-\frac{\sqrt7}{6}%2B\frac{-1-\sqrt3{\rm{i}}}{24}\sqrt[3]{52\sqrt7%2B12\sqrt{21}{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{24}\sqrt[3]{52\sqrt7-12\sqrt{21}{\rm{i}}}\right)\right]
\sqrt[7]{-2%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{28-84\sqrt3{\rm{i}}}%2B\frac{\sqrt7}{7}\left(14%2B\sqrt[3]{-2548%2B588\sqrt3{\rm{i}}}%2B\sqrt[3]{-2548-588\sqrt3{\rm{i}}}\right){\rm{i}}}%2B
\sqrt[7]{-2%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{28-84\sqrt3{\rm{i}}}%2B\frac{\sqrt7}{7}\left(-14%2B\sqrt[3]{2548%2B588\sqrt3{\rm{i}}}%2B\sqrt[3]{2548-588\sqrt3{\rm{i}}}\right){\rm{i}}}%2B
\sqrt[7]{-2%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{28%2B84\sqrt3{\rm{i}}}%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{28-84\sqrt3{\rm{i}}}%2B\frac{\sqrt7}{7}\left(14%2B\frac{-1%2B\sqrt3{\rm{i}}}{2}\sqrt[3]{-2548%2B588\sqrt3{\rm{i}}}%2B\frac{-1-\sqrt3{\rm{i}}}{2}\sqrt[3]{-2548-588\sqrt3{\rm{i}}}\right){\rm{i}}}\right\}}}\,](/2012-wikipedia_en_all_nopic_01_2012/I/baea7a5a65b5986a08b53b58bc6ed3d6.png)