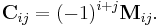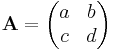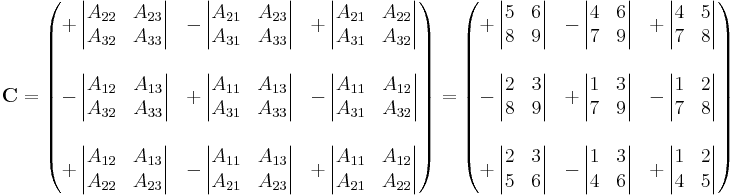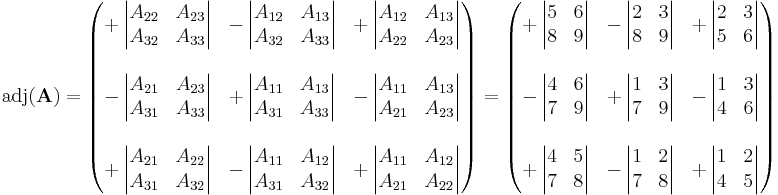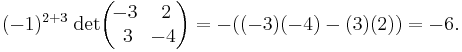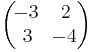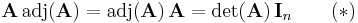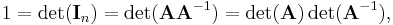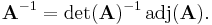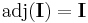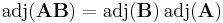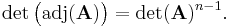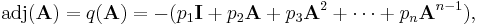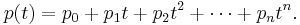Adjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions.
The adjugate has sometimes been called the "adjoint", but that terminology is ambiguous. Today, "adjoint" of a matrix normally refers to its corresponding adjoint operator, which is its conjugate transpose.
Contents |
Definition
Suppose R is a commutative ring and A is an n×n matrix with entries from R. The definition of the adjugate of A is a multi-step process:
- Define the (i,j) minor of A, denoted Mij, as the determinant of the (n − 1)×(n − 1) matrix that results from deleting row i and column j of A.
- Define the (i,j) cofactor of A as
- Define the cofactor matrix of A, as the n×n matrix C whose (i,j) entry is the (i,j) cofactor of A.
The adjugate of A is the transpose of the cofactor matrix of A:
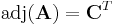 .
.
That is, the adjugate of A is the n×n matrix whose (i,j) entry is the (j,i) cofactor of A:
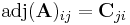 .
.
Examples
2 × 2 generic matrix
The adjugate of the 2 × 2 matrix
is
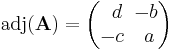 .
.
3 × 3 generic matrix
Consider the 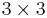 matrix
matrix
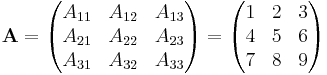 .
.
Its adjugate is the transpose of the cofactor matrix
So that we have
where
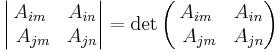 .
.
Note that the adjugate is the transpose of the cofactor matrix. Thus, for instance, the (3,2) entry of the adjugate is the (2,3) cofactor of A.
3 × 3 numeric matrix
As a specific example, we have
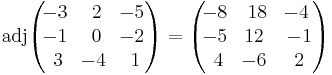 .
.
The −6 in the third row, second column of the adjugate was computed as follows:
Again, the (3,2) entry of the adjugate is the (2,3) cofactor of A. Thus, the submatrix
was obtained by deleting the second row and third column of the original matrix A.
Applications
As a consequence of Laplace's formula for the determinant of an n×n matrix A, we have
where 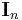 is the n×n identity matrix. Indeed, the (i,i) entry of the product A adj(A) is the scalar product of row i of A with row i of the cofactor matrix C, which is simply the Laplace formula for det(A) expanded by row i. Moreover, for i ≠ j the (i,j) entry of the product is the scalar product of row i of A with row j of C, which is the Laplace formula for the determinant of a matrix whose i and j rows are equal and is therefore zero.
is the n×n identity matrix. Indeed, the (i,i) entry of the product A adj(A) is the scalar product of row i of A with row i of the cofactor matrix C, which is simply the Laplace formula for det(A) expanded by row i. Moreover, for i ≠ j the (i,j) entry of the product is the scalar product of row i of A with row j of C, which is the Laplace formula for the determinant of a matrix whose i and j rows are equal and is therefore zero.
From this formula follows one of the most important results in matrix algebra: A matrix A over a commutative ring R is invertible if and only if det(A) is invertible in R.
For if A is an invertible matrix then
and if det(A) is a unit then (*) above shows that
See also Cramer's rule.
Properties
The adjugate has the properties
for all n×n matrices A and B.
The adjugate preserves transposition:
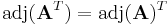 .
.
Furthermore
If p(t) = det(A − tI) is the characteristic polynomial of A and we define the polynomial q(t) = (p(0) − p(t))/t, then
where 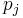 are the coefficients of p(t),
are the coefficients of p(t),
The adjugate also appears in the formula of the derivative of the determinant.
References
- Strang, Gilbert (1988). "Section 4.4: Applications of determinants". Linear Algebra and its Applications (3rd ed.). Harcourt Brace Jovanovich. pp. 231–232. ISBN 0-15-551005-3.
External links
- Matrix Reference Manual
- Online matrix calculator (determinant, track, inverse, adjoint, transpose) Compute Adjugate matrix up to order 8