Adapted process
In the study of stochastic processes, an adapted process (or non-anticipating process) is one that cannot "see into the future". An informal interpretation[1] is that X is adapted if and only if, for every realisation and every n, Xn is known at time n. The concept of an adapted process is essential, for instance, in the definition of the Itō integral, which only makes sense if the integrand is an adapted process.
Contents |
Definition
Let
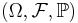 be a probability space;
be a probability space; be an index set with a total order
be an index set with a total order 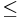 (often,
(often,  is
is 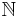 ,
, 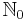 ,
, ![[0, T]](/2012-wikipedia_en_all_nopic_01_2012/I/b74093923941d33ee19becc5f4b48b25.png) or
or 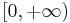 );
);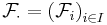 be a filtration of the sigma algebra
be a filtration of the sigma algebra 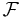 ;
; be a measurable space, the state space;
be a measurable space, the state space;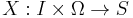 be a stochastic process.
be a stochastic process.
The process  is said to be adapted to the filtration
is said to be adapted to the filtration 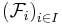 if the random variable
if the random variable 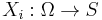 is a
is a 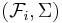 -measurable function for each
-measurable function for each 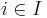 .[2]
.[2]
Examples
Consider a stochastic process X : [0, T] × Ω → R, and equip the real line R with its usual Borel sigma algebra generated by the open sets.
- If we take the natural filtration F•X, where FtX is the σ-algebra generated by the pre-images Xs−1(B) for Borel subsets B of R and times 0 ≤ s ≤ t, then X is automatically F•X-adapted. Intuitively, the natural filtration F•X contains "total information" about the behaviour of X up to time t.
- This offers a simple example of a non-adapted process X : [0, 2] × Ω → R: set Ft to be the trivial σ-algebra {∅, Ω} for times 0 ≤ t < 1, and Ft = FtX for times 1 ≤ t ≤ 2. Since the only way that a function can be measurable with respect to the trivial σ-algebra is to be constant, any process X that is non-constant on [0, 1] will fail to be F•-adapted. The non-constant nature of such a process "uses information" from the more refined "future" σ-algebras Ft, 1 ≤ t ≤ 2.