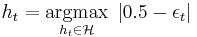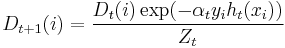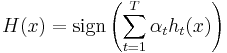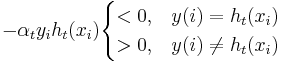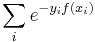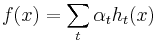AdaBoost
AdaBoost, short for Adaptive Boosting, is a machine learning algorithm, formulated by Yoav Freund and Robert Schapire.[1] It is a meta-algorithm, and can be used in conjunction with many other learning algorithms to improve their performance. AdaBoost is adaptive in the sense that subsequent classifiers built are tweaked in favor of those instances misclassified by previous classifiers. AdaBoost is sensitive to noisy data and outliers. In some problems, however, it can be less susceptible to the overfitting problem than most learning algorithms. The classifiers it uses can be weak (i.e., display a substantial error rate), but as long as their performance is not random (resulting in an error rate of 0.5 for binary classification), they will improve the final model. Even classifiers with an error rate higher than would be expected from a random classifier will be useful, since they will have negative coefficients in the final linear combination of classifiers and hence behave like their inverses.
AdaBoost generates and calls a new weak classifier in each of a series of rounds 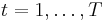 . For each call, a distribution of weights
. For each call, a distribution of weights 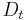 is updated that indicates the importance of examples in the data set for the classification. On each round, the weights of each incorrectly classified example are increased, and the weights of each correctly classified example are decreased, so the new classifier focuses on the examples which have so far eluded correct classification.
is updated that indicates the importance of examples in the data set for the classification. On each round, the weights of each incorrectly classified example are increased, and the weights of each correctly classified example are decreased, so the new classifier focuses on the examples which have so far eluded correct classification.
Contents |
The algorithm for the binary classification task
Given:
- training set:
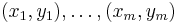 where
where 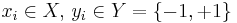
- number of iterations

Initialize 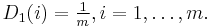
For 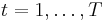 :
:
- From the family of weak classifiers ℋ, find the classifier
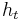 that maximizes the absolute value of the difference of the corresponding weighted error rate
that maximizes the absolute value of the difference of the corresponding weighted error rate 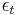 from 0.5 with respect to the distribution
from 0.5 with respect to the distribution 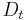 :
:
where 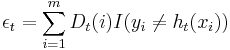 .
.
I is the indicator function.
- If
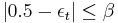 , where
, where  is a previously chosen threshold, then stop.
is a previously chosen threshold, then stop. - Choose
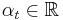 , typically
, typically 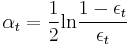 .
. - Update:
where 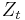 is the normalization factor:
is the normalization factor:
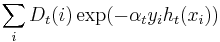
which ensures that 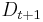 will be a probability distribution (i.e., the sum over all x equals one).
will be a probability distribution (i.e., the sum over all x equals one).
Output the final classifier:
Note that the equation to update the distribution 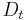 is constructed so that:
is constructed so that:
Thus, after selecting an optimal classifier 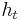 for the distribution
for the distribution 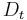 , the examples
, the examples 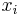 that the classifier
that the classifier 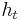 identified correctly are weighted less and those that it identified incorrectly are weighted more. Therefore, when the algorithm is testing the classifiers on the distribution
identified correctly are weighted less and those that it identified incorrectly are weighted more. Therefore, when the algorithm is testing the classifiers on the distribution 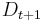 , it will select a classifier that better identifies those examples that the previous classifier missed.
, it will select a classifier that better identifies those examples that the previous classifier missed.
Statistical Understanding of Boosting
Boosting can be seen as minimization of a convex loss function over a convex set of functions.[2] Specifically, the loss being minimized is the exponential loss
and we are seeking a function
See also
- Bootstrap aggregating
- LPBoost
- GentleBoost
References
- ^ Yoav Freund, Robert E. Schapire. "A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting", 1995
- ^ T. Zhang, "Statistical behavior and consistency of classification methods based on convex risk minimization", Annals of Statistics 32 (1), pp. 56-85, 2004.
Implementations
- AdaBoost and the Super Bowl of Classifiers - A Tutorial on AdaBoost.
- Adaboost in C++, an implementation of Adaboost in C++ and boost by Antonio Gulli
- icsiboost, an open source implementation of Boostexter
- JBoost, a site offering a classification and visualization package, implementing AdaBoost among other boosting algorithms.
- MATLAB AdaBoost toolbox. Includes Real AdaBoost, Gentle AdaBoost and Modest AdaBoost implementations.
- A Matlab Implementation of AdaBoost
- milk for Python implements AdaBoost.
- MPBoost++, a C++ implementation of the original AdaBoost.MH algorithm and of an improved variant, the MPBoost algorithm.
- NPatternRecognizer , a fast machine learning algorithm library written in C#. It contains support vector machine, neural networks, bayes, boost, k-nearest neighbor, decision tree, ..., etc.
- OpenCV implementation of several boosting variants
- Into contains open source implementations of many AdaBoost and FloatBoost variants in C++.
External links
- Boosting.org, a site on boosting and related ensemble learning methods
- AdaBoost Presentation summarizing Adaboost (see page 4 for an illustrated example of performance)
- A Short Introduction to Boosting Introduction to Adaboost by Freund and Schapire from 1999
- A decision-theoretic generalization of on-line learning and an application to boosting Journal of Computer and System Sciences, no. 55. 1997 (Original paper of Yoav Freund and Robert E.Schapire where Adaboost is first introduced.)
- An applet demonstrating AdaBoost
- Ensemble Based Systems in Decision Making, R. Polikar, IEEE Circuits and Systems Magazine, vol.6, no.3, pp. 21–45, 2006. A tutorial article on ensemble systems including pseudocode, block diagrams and implementation issues for AdaBoost and other ensemble learning algorithms.
- Additive logistic regression: a statistical view of boosting by Jerome Friedman, Trevor Hastie, Robert Tibshirani. Paper introducing probabilistic theory for AdaBoost, and introducing GentleBoost