AdS/CFT correspondence
- For the relation of the AdS/CFT correspondence to the general context of string theory, see String theory.
In physics, the AdS/CFT correspondence (anti de Sitter/conformal field theory correspondence), sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more. The name suggests that the first space is the product of anti de Sitter space (AdS) with some closed manifold like sphere, orbifold, or noncommutative space, and that the quantum field theory is a conformal field theory (CFT).[1]
An example is the duality between Type IIB string theory on AdS5 × S5 space (a product of five dimensional AdS space with a five dimensional sphere) and a supersymmetric N = 4 Yang–Mills gauge theory (which is a conformal field theory) on the 4-dimensional boundary of AdS5. It is the most successful realization of the holographic principle, a speculative idea about quantum gravity originally proposed by Gerard 't Hooft and improved and promoted by Leonard Susskind.
The AdS/CFT correspondence was originally proposed by Juan Maldacena in late 1997.[2] Important aspects of the correspondence were given in articles by Steven Gubser, Igor Klebanov and Alexander Markovich Polyakov,[3] and by Edward Witten.[4] The correspondence has also been generalized to many other (non-AdS) backgrounds and their dual (non-conformal) theories. In about five years, Maldacena's article had 3000 citations and became one of the most important conceptual breakthroughs in theoretical physics of the 1990s, providing many new lines of research into both quantum gravity and quantum chromodynamics (QCD).
Contents |
Maldacena's example
Maldacena's initial observation was that a stack of N D3-branes in type IIB string theory has massless brane fields residing on it. With respect to the brane, they form Yang–Mills supermultiplets transforming under 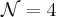 SUSY in 3+1D. The vector hypermultiplets form a gauge group
SUSY in 3+1D. The vector hypermultiplets form a gauge group  . This isn't quite a conformal field theory, even though it runs to one in the infrared once gravitation and string dynamics decouple. In the infrared, the
. This isn't quite a conformal field theory, even though it runs to one in the infrared once gravitation and string dynamics decouple. In the infrared, the 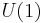 hypermultiplet decouples, but the
hypermultiplet decouples, but the  hypermultiplets remain interacting as the beta function is zero. The metric background is given by an extremal 3-brane black hole. The event horizon is infinitely far away; the distance to it diverges logarithmically. The near horizon geometry is approximately
hypermultiplets remain interacting as the beta function is zero. The metric background is given by an extremal 3-brane black hole. The event horizon is infinitely far away; the distance to it diverges logarithmically. The near horizon geometry is approximately  with the approximation becoming more and more exact closer to the horizon. Now, take the scaling limit as the string scale goes to zero with the string coupling kept fixed. All the string and gravitational dynamics decouple, and the U(1) hypermultiplet too. We are left with a bona fide
with the approximation becoming more and more exact closer to the horizon. Now, take the scaling limit as the string scale goes to zero with the string coupling kept fixed. All the string and gravitational dynamics decouple, and the U(1) hypermultiplet too. We are left with a bona fide 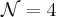 superconformal field theory. If we take the limit in which we are always in the near horizon region, the geometry becomes exactly
superconformal field theory. If we take the limit in which we are always in the near horizon region, the geometry becomes exactly  . A D3-brane has a self-dual charge under the self-dual NS 5-form flux. A stack of N of them gives rise to an integral flux of N over
. A D3-brane has a self-dual charge under the self-dual NS 5-form flux. A stack of N of them gives rise to an integral flux of N over 
Conformal boundary
A suitable Weyl transformation assures that AdS has a boundary. It turns out that this boundary is a conformal field theory having one fewer dimension. To make things more concrete, choose a particular coordinatization, the half-space coordinatization:
After a Weyl transformation ω = kz, we get
which has the Minkowski metric as the boundary at z = 0. This is called the conformal boundary.
Source fields
Basically, the correspondence runs as follows; if we deform the CFT by certain source fields by adding the source  , this will be dual to an AdS theory with a bulk field J with the boundary condition
, this will be dual to an AdS theory with a bulk field J with the boundary condition
where Δ is the conformal dimension of the local operator  and k is the number of covariant indices of
and k is the number of covariant indices of  minus the number of contravariant indices. Only gauge-invariant operators are allowed.
minus the number of contravariant indices. Only gauge-invariant operators are allowed.
Here, we have a dual source field for every gauge-invariant local operator we have.
Using generating functionals, the relation is expressed as
The left hand side is the vacuum expectation value of the time-ordered exponential of the operators over the conformal field theory. The right hand side is the quantum gravity generating functional with the given conformal boundary condition. The right hand side is evaluated by finding the classical solutions to the effective action subject to the given boundary conditions.
Some AdS5/CFT4 examples
The stress-energy operator on the CFT side is dual to the transverse components of the metric on the AdS side. Since the stress-energy operator has a conformal weight of 4, the AdS metric ought to go as 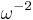 , which is true for AdS. Also, the graviton has to be massless, just as it should.
, which is true for AdS. Also, the graviton has to be massless, just as it should.
If there is a global internal symmetry G on the CFT side, its Noether current J will be dual to the transverse components of a gauge connection for a Yang–Mills gauge theory with G as the gauge group on the AdS side. Since J has a conformal weight of 3, the dual Yang–Mills gauge boson ought to have zero bulk mass, just as it should.
A scalar operator with conformal weight Δ will be dual to a scalar bulk field with a bulk mass of  .
.
Particles
A CFT bound state of size r is dual to a bulk particle approximately localized at z=r.
Supersymmetry
AdS5/CFT4
We need to match up conformal supersymmetry in 4D with AdS supersymmetry in 5D. The symmetry supergroups in both cases happen to match up, as they should. There are  real SUSY generators and the bosonic part consists of the conformal AdS group Spin(4,2) times an internal group
real SUSY generators and the bosonic part consists of the conformal AdS group Spin(4,2) times an internal group  . See superconformal algebra for more details.
. See superconformal algebra for more details.
For the case 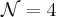 , we have 32 real SUSY generators and an internal group
, we have 32 real SUSY generators and an internal group  . Now,
. Now,  and Spin(6) is the isometry group of S5 with spinorial fields. The bosonic spatial isometry group of
and Spin(6) is the isometry group of S5 with spinorial fields. The bosonic spatial isometry group of  is
is 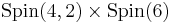 .
.
In  10D SUSY, we have 32 real SUSY generators. In a generic curved spacetime, some of the SUSY generators will be broken but in the special compactification of
10D SUSY, we have 32 real SUSY generators. In a generic curved spacetime, some of the SUSY generators will be broken but in the special compactification of  with both factors having the same radius, we are left 32 real unbroken generators. However, the bosonic spatial isometries with 55 generators in the flat case is now broken to
with both factors having the same radius, we are left 32 real unbroken generators. However, the bosonic spatial isometries with 55 generators in the flat case is now broken to 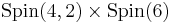 with 30 generators.
with 30 generators.  also has a
also has a 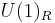 symmetry and this is identified with
symmetry and this is identified with  .
.
The source of the curvature lies in the nonzero value of a self-dual 5-form flux belonging to the SUGRA multiplet. The integral of this 5-flux over S5 has to be a nonzero integer (if it's zero, we have no stress-energy tensor). Because the part of the 5-flux lying in AdS5 contains a time component, it gives rise to negative curvature. The part of the 5-flux lying in S5 doesn't have a time component, and so, it gives rise to a positive curvature.
The SUGRA multiplet also contains a dilaton and axion field. They correspond to the gauge field coupling and theta angle of the dual superYang–Mills theory.
AdS4/CFT3
There are 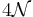 real SUSY generators with
real SUSY generators with 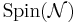 as the obligatory R-symmetry.
as the obligatory R-symmetry.
11D 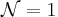 supergravity contains 32 real SUSY generators. There is a particular compactification,
supergravity contains 32 real SUSY generators. There is a particular compactification, 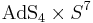 , the Freund–Rubin compactification, which preserves all 32 real generators. The bosonic isometry group is reduced to
, the Freund–Rubin compactification, which preserves all 32 real generators. The bosonic isometry group is reduced to  . After a Kaluza–Klein decomposition over S7, we get
. After a Kaluza–Klein decomposition over S7, we get  SUSY. A 7-form magnetic flux is present over S7. Its integral over S7 has to be integer and nonzero.
SUSY. A 7-form magnetic flux is present over S7. Its integral over S7 has to be integer and nonzero.
Applications
A plethora of papers is found in the literature which uses techniques of ADS CFT to understand strongly coupled system such as RHIC and condensed matter systems.
Other topics
Certain "higher spin gauge theories" on AdS space appear to be holographically dual to a CFT with O(N) symmetry.[5] This has been called the Klebanov–Polyakov correspondence.
The AdS/CFT correspondence should not be confused with algebraic holography or "Rehren duality"; although these are sometimes identified with AdS/CFT, string theorists agree that they are different things.[6][7][8]
See also
References
- ^ For an authoritative review, see Ofer Aharony, Steven S. Gubser, Juan Maldacena, Hirosi Ooguri and Yaron Oz (2000). "Large N field theories, string theory and gravity". Physics Reports 323: 183–386. arXiv:hep-th/9905111. doi:10.1016/S0370-1573(99)00083-6. (Shorter lectures by Maldacena, based on that review.)
- ^ Juan M. Maldacena (1998). "The Large N limit of superconformal field theories and supergravity". Advances in Theoretical and Mathematical Physics 2: 231–252. arXiv:hep-th/9711200. Bibcode 1998AdTMP...2..231M.
- ^ S. S. Gubser, I. R. Klebanov and A. M. Polyakov (1998). "Gauge theory correlators from non-critical string theory". Physics Letters B428: 105–114. arXiv:hep-th/9802109. Bibcode 1998PhLB..428..105G. doi:10.1016/S0370-2693(98)00377-3.
- ^ Edward Witten (1998). "Anti-de Sitter space and holography". Advances in Theoretical and Mathematical Physics 2: 253–291. arXiv:hep-th/9802150. Bibcode 1998hep.th....2150W.
- ^ Lubos Motl, "Holography: Vasiliev's higher-spin theories and O(N) models", The Reference Frame, 20 February 2010.
- ^ Jacques Distler, "Rehren Duality", Musings, 16 October 2006 (accessed 22 July 2009).
- ^ Urs Schreiber, "Making AdS/CFT Precise", The n-Category Café, 22 July 2007 (accessed 22 July 2009).
- ^ Karl-Henning Rehren (2005). "QFT Lectures on AdS-CFT". In B. Dragovich et al.. Proceedings of the 3rd Summer School in Modern Mathematical Physics. 2004 Zlatibor Summer School on Modern Mathematical Physics. Belgrade: Institute of Physics. pp. 95–118. arXiv:hep-th/0411086.
External links
- AdS/CFT correspondence on arxiv.org.
- The Illusion of Gravity – Juan Maldacena, Scientific American.
- University of Michigan Lecture
- Professor Hirosi Ooguri's notes
- Meeting on the subject
- Database of articles; Supersymmetric Gauge Theories and the AdS/CFT Correspondence
- Shadow World. The state of the AdS/CFT conjecture on its 10th anniversary. Science News magazine, November 17, 2007.
|
|||||||||||||||||||||||||||||||||||||||


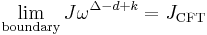
![\left\langle \mathcal{T}\left\{ \exp\left(\int d^dx J_{4D}(x)\mathcal{O}(x)\right) \right\} \right\rangle_{CFT} = Z_{AdS}\left[\lim_{\text{boundary}} J \omega^{\Delta-d%2Bk} = J_{4D}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/51af61fefe676a7d1e2f97c22b33cc2b.png)