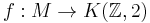Abstract nonsense
In mathematics, abstract nonsense, general abstract nonsense, and general nonsense are terms used facetiously by some mathematicians to describe certain kinds of arguments and methods related to category theory. (Very) roughly speaking, category theory is the study of the general form of mathematical theories, without regard to their content. As a result, a proof that relies on category theoretic ideas often seems slightly out of context to those who are not used to such abstraction, sometimes to the extent that it resembles a comical non sequitur. Such proofs are sometimes dubbed “abstract nonsense” as a light-hearted way of alerting people to their abstract nature.
More generally, “abstract nonsense” may refer to any proof (humorous or not) that uses primarily category theoretic methods, or even to the study of category theory itself. Note that referring to an argument as "abstract nonsense" is not supposed to be a derogatory expression, and is actually often a compliment regarding the sophistication of the argument.[1][2]
Contents |
History
The term predates the foundation of category theory as a subject itself. Referring to a joint paper with Samuel Eilenberg that introduced the notion of a "category" in 1942, Saunders Mac Lane wrote the subject was 'then called "general abstract nonsense"'.[3] The term is often used to describe the application of category theory and its techniques to less abstract domains.[4][5]
The term is believed to have been coined by the mathematician Norman Steenrod,[6][7][8] himself one of the developers of the categorical point of view. This term is used by practitioners as an indication of mathematical sophistication (or possession of a deeper perspective) rather than as a derogatory designation.[2]
Certain ideas and constructions in mathematics display a uniformity throughout many domains. The unifying theme is category theory. When their audience can be assumed to be familiar with the general form of such arguments, mathematicians will use the expression Such and such is true by abstract nonsense rather than provide an elaborate explanation of particulars.[1]
Examples
Typical instances are arguments involving diagram chasing, application of the definition of universal property, definition of natural transformations between functors, use of the Yoneda lemma, arguments exploiting classifying spaces, and so on.
To spell out a concrete example, consider a 3-manifold M with positive Betti number. One would like to show that M admits a map to the 2-sphere which is "non-trivial", i.e. non-homotopic to the constant map. By a general nonsense argument, there is a map
to the Eilenberg-MacLane space, corresponding to a non-trivial element in H2(M). Since K(Z,2) is a complex projective space and the latter admits a skeleton structure with no cells in odd dimensions, we can apply the cellular approximation theorem to conclude that the map f can be pushed down to the 2-skeleton, which happens to be the 2-sphere.
Though this proof establishes the truth of the statement in question, the proof technique has little to do with the topology or geometry of the 2-sphere, let alone 3-manifolds. The result is that the proof offers little geometric insight into the nature of such a map. On the other hand, the proof is surprisingly short and clean, and a “hands-on” approach involving the physical construction of such a map would be potentially laborious. A reader expecting a long, difficult proof might be surprised—or even delighted—by this bit of general nonsense.
Notes and references
- ^ a b Macura, Wiktor K., "Abstract Nonsense" from MathWorld.
- ^ a b Michael Monastyrsky, Some Trends in Modern Mathematics and the Fields Medal. Can. Math. Soc. Notes, March and April 2001, Volume 33, nos. 2 and 3. Online version available at http://www.fields.utoronto.ca/aboutus/FieldsMedal_Monastyrsky.pdf.
- "In algebra, the term “abstract nonsense” has a definite meaning without any pejorative connotation."
- ^ Saunders Mac Lane. "The PNAS way back then". Proc. Natl. Acad. Sci. USA Vol. 94, pp. 5983–5985, June 1997.
- "The first of these papers is a more striking case; it introduced the very abstract idea of a "category"—a subject then called "general abstract nonsense"!"
- ^ An Application of Abstract Nonsense to Surface Area, Harriet Lord
- ^ Abstract Nonsense for Functional Programmers, Edsko de Vries
- ^ Colin McLarty, The Uses and Abuses of the History of Topos Theory, Brit. J. Phil. Sci, 41 (1990) p 355.
- "Steenrod jokingly tagged category theory 'abstract nonsense' and made it central to his axiomatics for homology"
- ^ Joseph Rotman, "An Introduction to Homological Algebra, by Charles A. Weibel" (book review), Bull. Amer. Math. Soc., 33:4 (Oct. 1996) 473–476.
- "The self-deprecating phrase general abstract nonsense (due to Steenrod) was promulgated by Eilenberg and Mac Lane, two of the major innovators of homological algebra, to highlight this aspect of the subject."
- ^ Serge Lang, "Algebra" Second Edition, Addison Wesley, 1984, p 175