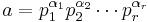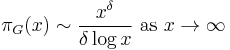Abstract analytic number theory
Abstract analytic number theory is a branch of mathematics which takes the ideas and techniques of classical analytic number theory and applies them to a variety of different mathematical fields. The classical prime number theorem serves as a prototypical example, and the emphasis is on abstract asymptotic distribution results. The theory was invented and developed by John Knopfmacher in the early 1970s.
Contents |
Arithmetic semigroups
The fundamental notion involved is that of an arithmetic semigroup, which is a commutative monoid G satisfying the following properties:
- There exists a countable subset (finite or countably infinite) P of G, such that every element a ≠ 1 in G has a unique factorisation of the form
- where the pi are distinct elements of P, the αi are positive integers, r may depend on a, and two factorisations are considered the same if they differ only by the order of the factors indicated. The elements of P are called the primes of G.
- There exists a real-valued norm mapping
 on G such that
on G such that
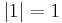
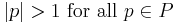
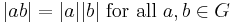
- The total number
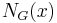 of elements
of elements 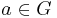 of norm
of norm 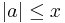 is finite, for each real
is finite, for each real 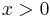 .
.
Examples
- The prototypical example of an arithmetic semigroup is the multiplicative semigroup of positive integers G = Z+ = {1, 2, 3, ...}, with subset of rational primes P = {2, 3, 5, ...}. Here, the norm of an integer is simply
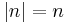 , so that
, so that 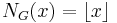 , the greatest integer not exceeding x.
, the greatest integer not exceeding x. - If K is an algebraic number field, i.e. a finite extension of the field of rational numbers Q, then the set G of all nonzero ideals in the ring of integers OK of K forms an arithmetic semigroup with identity element OK and the norm of an ideal I is given by the cardinality of the quotient ring OK/I. In this case, the appropriate generalisation of the prime number theorem is the Landau prime ideal theorem, which describes the asymptotic distribution of the ideals in OK.
- Various arithmetical categories which satisfy a theorem of Krull-Schmidt type can be considered. In all these cases, the elements of G are isomorphism classes in an appropriate category, and P consists of all isomorphism classes of indecomposable objects, i.e. objects which cannot be decomposed as a direct product of nonzero objects. Some typical examples are the following.
- The category of all finite abelian groups under the usual direct product operation and norm mapping
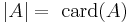 . The indecomposable objects are the cyclic groups of prime power order.
. The indecomposable objects are the cyclic groups of prime power order. - The category of all compact simply-connected globally symmetric Riemannian manifolds under the Riemannian product of manifolds and norm mapping
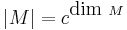 , where c > 1 is fixed, and dim M denotes the manifold dimension of M. The indecomposable objects are the compact simply-connected irreducible symmetric spaces.
, where c > 1 is fixed, and dim M denotes the manifold dimension of M. The indecomposable objects are the compact simply-connected irreducible symmetric spaces. - The category of all pseudometrisable finite topological spaces under the topological sum and norm mapping
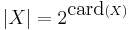 . The indecomposable objects are the connected spaces.
. The indecomposable objects are the connected spaces.
- The category of all finite abelian groups under the usual direct product operation and norm mapping
Methods and techniques
The use of arithmetic functions and zeta functions is extensive. The idea is to extend the various arguments and techniques of arithmetic functions and zeta functions in classical analytic number theory to the context of an arbitrary arithmetic semigroup which may satisfy one or more additional axioms. Such a typical axiom is the following, usually called "Axiom A" in the literature:
- Axiom A. There exist positive constants A and
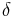 , and a constant
, and a constant  with
with 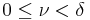 , such that
, such that 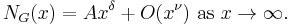
For any arithmetic semigroup which satisfies Axiom A, we have the following abstract prime number theorem:
where πG(x) = total number of elements p in P of norm |p| ≤ x.
The notion of arithmetical formation provides a generalisation of the ideal class group in algebraic number theory and allows for abstract asymptotic distribution results under constraints. In the case of number fields, for example, this is Chebotarev's density theorem.
References
- John Knopfmacher (1975). Abstract Analytic Number Theory. Dover Publishing. ISBN 0-486-66344-2.
- Hugh L. Montgomery; Robert C. Vaughan (2007). Multiplicative number theory I. Classical theory. Cambridge tracts in advanced mathematics. 97. p. 278. ISBN 0-521-84903-9.