Abstract Wiener space
An abstract Wiener space is a mathematical object in measure theory, used to construct a "decent" (strictly positive and locally finite) measure on an infinite-dimensional vector space. It is named after the American mathematician Norbert Wiener. Wiener's original construction only applied to the space of real-valued continuous paths on the unit interval, known as classical Wiener space; Leonard Gross provided the generalization to the case of a general separable Banach space.
Contents |
Definition
Let H be a separable Hilbert space. Let E be a separable Banach space. Let i : H → E be an injective continuous linear map with dense image (i.e., the closure of i(H) in E is E itself) that radonifies the canonical Gaussian cylinder set measure γH on H. Then the triple (i, H, E) (or simply i : H → E) is called an abstract Wiener space. The measure γ induced on E is called the abstract Wiener measure of i : H → E.
The Hilbert space H is sometimes called the Cameron–Martin space or reproducing kernel Hilbert space.
Some sources (e.g. Bell (2006)) consider H to be a densely embedded Hilbert subspace of the Banach space E, with i simply the inclusion of H into E. There is no loss of generality in taking this "embedded spaces" viewpoint instead of the "different spaces" viewpoint given above.
Properties
- γ is a Borel measure: it is defined on the Borel σ-algebra generated by the open subsets of E.
- γ is a Gaussian measure in the sense that f∗(γ) is a Gaussian measure on R for every linear functional f ∈ E∗, f ≠ 0.
- Hence, γ is strictly positive and locally finite.
- If E is a finite-dimensional Banach space, we may take E to be isomorphic to Rn for some n ∈ N. Setting H = Rn and i : H → E to be the canonical isomorphism gives the abstract Wiener measure γ = γn, the standard Gaussian measure on Rn.
- The behaviour of γ under translation is described by the Cameron–Martin theorem.
- Given two abstract Wiener spaces i1 : H1 → E1 and i2 : H2 → E2, one can show that γ12 = γ1 ⊗ γ2. In full:
- i.e., the abstract Wiener measure γ12 on the Cartesian product E1 × E2 is the product of the abstract Wiener measures on the two factors E1 and E2.
- If H (and E) are infinite dimensional, then the image of H has measure zero: γ(i(H)) = 0. This fact is a consequence of Kolmogorov's zero-one law.
Example: Classical Wiener space
Arguably the most frequently-used abstract Wiener space is the space of continuous paths, and is known as classical Wiener space. This is the abstract Wiener space with
with inner product
E = C0([0, T]; Rn) with norm
and i : H → E the inclusion map. The measure γ is called classical Wiener measure or simply Wiener measure.
See also
References
- Bell, Denis R. (2006). The Malliavin calculus. Mineola, NY: Dover Publications Inc.. p. x+113. ISBN 0-486-44994-7. MR2250060. (See section 1.1)
- Gross, Leonard (1967). "Abstract Wiener spaces". Proc. Fifth Berkeley Sympos. Math. Statist. and Probability (Berkeley, Calif., 1965/66), Vol. II: Contributions to Probability Theory, Part 1. Berkeley, Calif.: Univ. California Press. pp. 31–42. MR0212152. http://projecteuclid.org/euclid.bsmsp/1200513262.
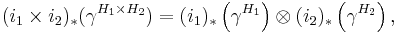
![H�:= L_{0}^{2, 1} ([0, T]; \mathbb{R}^{n})�:= \{ \text{paths starting at 0 with first derivative} \in L^{2} \}](/2012-wikipedia_en_all_nopic_01_2012/I/057d2005d691194bc3a39212e0adb785.png)
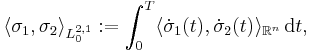
![\| \sigma \|_{C_{0}}�:= \sup_{t \in [0, T]} \| \sigma (t) \|_{\mathbb{R}^{n}},](/2012-wikipedia_en_all_nopic_01_2012/I/17a9fa993d90a0be7ae5dffd2caa8ab5.png)