Absolutely convex set
A set C in a real or complex vector space is said to be absolutely convex if it is convex and balanced.
Contents |
Properties
A set  is absolutely convex if and only if for any points
is absolutely convex if and only if for any points 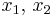 in
in  and any numbers
and any numbers 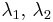 satisfying
satisfying 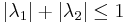 the sum
the sum 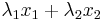 belongs to
belongs to  .
.
Since the intersection of any collection of absolutely convex sets is absolutely convex then for any subset A of a vector space one can define its absolutely convex hull to be the intersection of all absolutely convex sets containing A.
Absolutely convex hull
The absolutely convex hull of the set A assumes the following representation
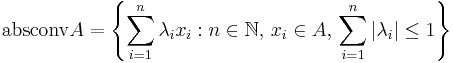 .
.
References
- Robertson, A.P.; W.J. Robertson (1964). Topological vector spaces. Cambridge Tracts in Mathematics. 53. Cambridge University Press. pp. 4–6.
See also
- vector (geometric), for vectors in physics
- Vector field