n-sphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in (n + 1)-dimensional Euclidean space which are at distance r from a central point, where the radius r may be any positive real number. In symbols:
It is an n-dimensional manifold in Euclidean (n + 1)-space. In particular, a 0-sphere is a pair of points that are the ends of a line segment, a 1-sphere is a circle in the plane, and a 2-sphere is an ordinary sphere in three-dimensional space. Spheres of dimension n > 2 are sometimes called hyperspheres, with 3-spheres sometimes known as glomes. The n-sphere of unit radius centered at the origin is called the unit n-sphere, denoted Sn. The unit n-sphere is often referred to as the n-sphere. An n-sphere is the surface or boundary of an (n + 1)-dimensional ball, and is an n-dimensional manifold. For n ≥ 2, the n-spheres are the simply connected n-dimensional manifolds of constant, positive curvature. The n-spheres admit several other topological descriptions: for example, they can be constructed by gluing two n-dimensional Euclidean spaces together, by identifying the boundary of an n-cube with a point, or (inductively) by forming the suspension of an (n − 1)-sphere.
Contents |
Description
For any natural number n, an n-sphere of radius r is defined as the set of points in (n + 1)-dimensional Euclidean space that are at distance r from some fixed point c, where r may be any positive real number and where c may be any point in (n + 1)-dimensional space. In particular:
- a 0-sphere is a pair of points {c − r, c + r}, and is the boundary of a line segment (1-ball).
- a 1-sphere is a circle of radius r centered at c, and is the boundary of a disk (2-ball).
- a 2-sphere is an ordinary 2-dimensional sphere in 3-dimensional Euclidean space, and is the boundary of an ordinary ball (3-ball).
- a 3-sphere is a sphere in 4-dimensional Euclidean space.
Euclidean coordinates in (n + 1)-space
The set of points in (n + 1)-space: (x1,x1,x2,…,xn+1) that define an n-sphere, (Sn) is represented by the equation:
where c is a center point, and r is the radius.
The above n-sphere exists in (n + 1)-dimensional Euclidean space and is an example of an n-manifold. The volume form ω of an n-sphere of radius r is given by
where * is the Hodge star operator; see Flanders (1989, §6.1) for a discussion and proof of this formula in the case r = 1. As a result, 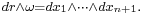
n-ball
-
Main article: ball (mathematics)
The space enclosed by an n-sphere is called an (n + 1)-ball. An (n + 1)-ball is closed if it includes the n-sphere, and it is open if it does not include the n-sphere.
Specifically:
- A 1-ball, a line segment, is the interior of a (0-sphere).
- A 2-ball, a disk, is the interior of a circle (1-sphere).
- A 3-ball, an ordinary ball, is the interior of a sphere (2-sphere).
- A 4-ball, is the interior of a 3-sphere, etc.
Topological description
Topologically, an n-sphere can be constructed as a one-point compactification of n-dimensional Euclidean space. Briefly, the n-sphere can be described as 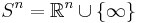 , which is n-dimensional Euclidean space plus a single point representing infinity in all directions. In particular, if a single point is removed from an n-sphere, it becomes homeomorphic to
, which is n-dimensional Euclidean space plus a single point representing infinity in all directions. In particular, if a single point is removed from an n-sphere, it becomes homeomorphic to 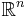 . This forms the basis for stereographic projection. [1]
. This forms the basis for stereographic projection. [1]
Volume and surface area
The  -volume of an
-volume of an  -sphere of radius
-sphere of radius  or, equivalently, the surface area of an
or, equivalently, the surface area of an 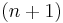 -ball of radius
-ball of radius  is:
is:
The  -volume of a
-volume of a  -ball of radius
-ball of radius  :
:
The 1-sphere of radius R is the circle of radius R in the Euclidean plane, and this has circumference (1-dimensional measure)
The region enclosed by the 1-sphere is the 2-ball, or disk of radius R, and this has area (2-dimensional measure)
Analogously, in 3-dimensional Euclidean space, the surface area (2-dimensional measure) of the 2-sphere of radius R is given by
and the volume enclosed is the volume (3-dimensional measure) of the 3-ball, and is given by
In general, the volume, in n-dimensional Euclidean space, of the n-ball of radius R is proportional to the nth power of the R:
where the constant of proportionality, the volume of the unit n-ball, is given by
where 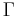 is the gamma function. For even n, this reduces to
is the gamma function. For even n, this reduces to
and since
for odd n,
where 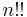 denotes the double factorial.
denotes the double factorial.
The "surface area", or properly the (n − 1)-dimensional volume, of the (n−1)-sphere at the boundary of the n-ball is
The following relationships hold between the n-spherical surface area and volume:
This leads to the recurrence relations:
The recurrence relation for 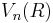 can be proved via integration with 2-dimensional polar coordinates:
can be proved via integration with 2-dimensional polar coordinates:
Hyperspherical coordinates
We may define a coordinate system in an n-dimensional Euclidean space which is analogous to the spherical coordinate system defined for 3-dimensional Euclidean space, in which the coordinates consist of a radial coordinate, 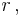 and n − 1 angular coordinates
and n − 1 angular coordinates  where
where 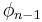 ranges over
ranges over 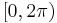 radians (or over [0, 360) degrees) and the other angles range over
radians (or over [0, 360) degrees) and the other angles range over ![[0, \pi] \,](/2012-wikipedia_en_all_nopic_01_2012/I/034433dd3d56b07927de450b1a2b0acd.png) radians (or over [0, 180] degrees). If
radians (or over [0, 180] degrees). If 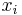 are the Cartesian coordinates, then we may compute
are the Cartesian coordinates, then we may compute  from
from  with:
with:
Except in the special cases described below, the inverse transformation is unique:
where if 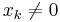 for some
for some  but all of
but all of  are zero then
are zero then 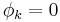 when
when 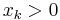 , and
, and 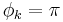 radians (180 degrees) when
radians (180 degrees) when 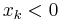 .
.
There are some special cases where the inverse transform is not unique; 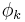 for any
for any  will be ambiguous whenever all of
will be ambiguous whenever all of 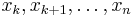 are zero; in this case
are zero; in this case 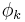 may be chosen to be zero.
may be chosen to be zero.
Note that a half-angle formula is used for 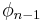 because the more straightforward
because the more straightforward 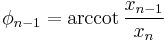 is too small by an addend of π when
is too small by an addend of π when 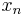 < 0.
< 0.
Hyperspherical volume element
Expressing the angular measures in radians, the volume element in n-dimensional Euclidean space will be found from the Jacobian of the transformation:
and the above equation for the volume of the n-ball can be recovered by integrating:
The volume element of the (n-1)–sphere, which generalizes the area element of the 2-sphere, is given by
The natural choice of an orthogonal basis over the angular coordinates is a product of ultraspherical polynomials,
for j = 1, 2, ..., n − 2, and the e isφj for the angle j = n − 1 in concordance with the spherical harmonics.
Stereographic projection
-
Main article: Stereographic projection
Just as a two dimensional sphere embedded in three dimensions can be mapped onto a two-dimensional plane by a stereographic projection, an n-sphere can be mapped onto an n-dimensional hyperplane by the n-dimensional version of the stereographic projection. For example, the point ![\ [x,y,z]](/2012-wikipedia_en_all_nopic_01_2012/I/96155b1bc331454ce48057c12f9596a1.png) on a two-dimensional sphere of radius 1 maps to the point
on a two-dimensional sphere of radius 1 maps to the point ![\left[\frac{x}{1-z},\frac{y}{1-z}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/3250235e1791f957399ea682325dd273.png) on the
on the 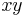 plane. In other words,
plane. In other words,
Likewise, the stereographic projection of an n-sphere 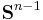 of radius 1 will map to the
of radius 1 will map to the 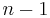 dimensional hyperplane
dimensional hyperplane 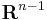 perpendicular to the
perpendicular to the 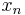 axis as
axis as
Generating random points
Uniformly at random from the (n − 1)-sphere
To generate uniformly distributed random points on the (n − 1)-sphere (i.e., the surface of the n-ball), Marsaglia (1972) gives the following algorithm.
Generate an n-dimensional vector of normal deviates (it suffices to use N(0, 1), although in fact the choice of the variance is arbitrary), 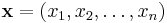 .
.
Now calculate the "radius" of this point, 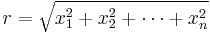 .
.
The vector 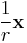 is uniformly distributed over the surface of the unit n-ball.
is uniformly distributed over the surface of the unit n-ball.
Examples
For example, when n = 2 the normal distribution exp(−x12) when expanded over another axis exp(−x22) after multiplication takes the form exp(−x12−x22) or exp(−r2) and so is only dependent on distance from the origin.
Alternatives
Another way to generate a random distribution on a hypersphere is to make a uniform distribution over a hypercube that includes the unit hyperball, exclude those points that are outside the hyperball, then project the remaining interior points outward from the origin onto the surface. This will give a uniform distribution, but it is necessary to remove the exterior points. As the relative volume of the hyperball to the hypercube decreases very rapidly with dimension, this procedure will succeed with high probability only for fairly small numbers of dimensions.
Wendel's theorem gives the probability that all of the points generated will lie in the same half of the hypersphere.
Uniformly at random from the n-ball
With a point selected from the surface of the n-ball uniformly at random, one needs only a radius to obtain a point uniformly at random within the n-ball. If u is a number generated uniformly at random from the interval [0, 1] and x is a point selected uniformly at random from the surface of the n-ball then u1/nx is uniformly distributed over the entire unit n-ball.
Specific spheres
- 0-sphere
- The pair of points {±R} with the discrete topology for some R > 0. The only sphere that is disconnected. Has a natural Lie group structure; isomorphic to O(1). Parallelizable.
- 1-sphere
- Also known as the circle. Has a nontrivial fundamental group. Abelian Lie group structure U(1); the circle group. Topologically equivalent to the real projective line, RP1. Parallelizable. SO(2) = U(1).
- 2-sphere
- Also known as the sphere. Complex structure; see Riemann sphere. Equivalent to the complex projective line, CP1. SO(3)/SO(2).
- 3-sphere
- Parallelizable, Principal U(1)-bundle over the 2-sphere, Lie group structure Sp(1), where also
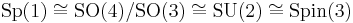 .
.- 4-sphere
- Equivalent to the quaternionic projective line, HP1. SO(5)/SO(4).
- 5-sphere
- Principal U(1)-bundle over CP2. SO(6)/SO(5) = SU(3)/SU(2).
- 6-sphere
- Almost complex structure coming from the set of pure unit octonions. SO(7)/SO(6) = G2/SU(3).
- 7-sphere
- Topological quasigroup structure as the set of unit octonions. Principal Sp(1)-bundle over S4. Parallelizable. SO(8)/SO(7) = SU(4)/SU(3) = Sp(2)/Sp(1) = Spin(7)/G2 = Spin(6)/SU(3). The 7-sphere is of particular interest since it was in this dimension that the first exotic spheres were discovered.
- 8-sphere
- Equivalent to the octonionic projective line OP1.
- 23-sphere
- A highly dense sphere-packing is possible in 24 dimensional space, which is related to the unique qualities of the Leech lattice.
See also
- Affine sphere
- Conformal geometry
- Deriving the volume of an n-ball
- Inversive geometry
- Homology sphere
- Homotopy groups of spheres
- Homotopy sphere
- Hyperbolic group
- Hypercube
- Loop (topology)
- Manifold
- Möbius transformation
- Orthogonal group
- Spherical cap
Notes
- ^ James W. Vick (1994). Homology theory, p. 60. Springer
References
- Flanders, Harley (1989). Differential forms with applications to the physical sciences. New York: Dover Publications. ISBN 978-0-486-66169-8..
- Moura, Eduarda; Henderson, David G. (1996). Experiencing geometry: on plane and sphere. Prentice Hall. ISBN 978-0-13-373770-7. http://www.math.cornell.edu/~henderson/books/eg00 (Chapter 20: 3-spheres and hyperbolic 3-spaces.)
- Weeks, Jeffrey R. (1985). The Shape of Space: how to visualize surfaces and three-dimensional manifolds. Marcel Dekker. ISBN 978-0-8247-7437-0 (Chapter 14: The Hypersphere)
- Marsaglia, G. (1972). "Choosing a Point from the Surface of a Sphere". Ann. Math. Stat. 43 (2): 645–646. doi:10.1214/aoms/1177692644.
- Huber, Greg (1982). "Gamma function derivation of n-sphere volumes". Am. Math. Monthly 89 (5): 301–302. doi:10.2307/2321716. JSTOR 2321716. MR1539933.
External links
|
|||||||||||||||||
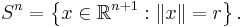
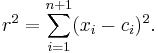
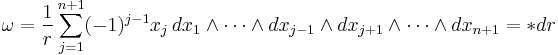
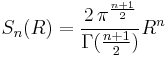
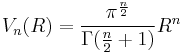

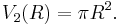
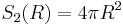
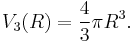

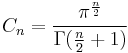
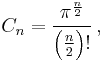
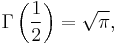
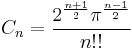
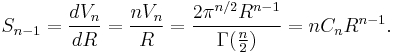
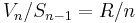
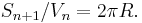
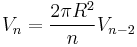
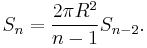
![\begin{align}
V_n (R)
& = \int_0^R \int_0^{2\pi} V_{n-2}(\sqrt{R^2-r^2}) \, r \, d\theta \, dr \\[6pt]
& = \int_0^R \int_0^{2\pi} C_{n-2} (R^2-r^2)^{n/2-1}\, r \, d\theta \, dr \\[6pt]
& = 2 \pi C_{n-2} \int_{0}^{R} (R^2-r^2)^{n/2-1}\, r \, dr \\[6pt]
& = 2 \pi C_{n-2} \left[ -\frac{1}{n}(R^2-r^2)^{n/2} \right]^{r=R}_{r=0} \\[6pt]
& = 2 \pi C_{n-2} \frac{R^n}{n} = \frac{2 \pi R^2}{n} V_{n-2}(R).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/02dd5df12c797436eea012b186d52ebe.png)
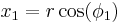
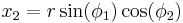
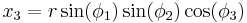

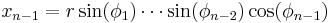
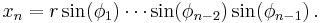
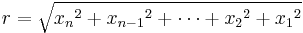
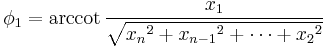
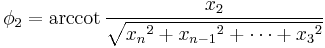
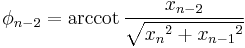
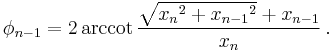
![\begin{align}
d_{\mathbb{R}^n}V & =
\left|\det\frac{\partial (x_i)}{\partial(r,\phi_j)}\right|
dr\,d\phi_1 \, d\phi_2\cdots d\phi_{n-1} \\[6pt]
& = r^{n-1}\sin^{n-2}(\phi_1)\sin^{n-3}(\phi_2)\cdots \sin(\phi_{n-2})\,
dr\,d\phi_1 \, d\phi_2\cdots d\phi_{n-1}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3a7e3278519f92f1b40e0b2c4b673e51.png)
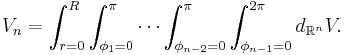
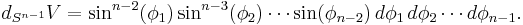
![\begin{align}
& {} \quad \int_0^\pi \sin^{n-j-1}(\phi_j) C_s^{((n-j-1)/2)}(\cos \phi_j)C_{s'}^{((n-j-1)/2)}(\cos\phi_j) \, d\phi_j \\[6pt]
& = \frac{\pi 2^{3-n%2Bj}\Gamma(s%2Bn-j-1)}{s!(2s%2Bn-j-1)\Gamma^2((n-j-1)/2)}\delta_{s,s'}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/04f260e10ce9625af6e38fdd25c42333.png)
![\ [x,y,z] \mapsto \left[\frac{x}{1-z},\frac{y}{1-z}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/95c84f377fabe5ebd1e04589631ad42f.png)
![[x_1,x_2,\ldots,x_n] \mapsto \left[\frac{x_1}{1-x_n},\frac{x_2}{1-x_n},\ldots,\frac{x_{n-1}}{1-x_n}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/70fe520ba200d5143473a38d28070972.png)