600-cell

600-cell

Schlegel diagram, vertex-centered
(vertices and edges)
Type Convex regular 4-polytope
Schläfli symbol {3,3,5}
Coxeter-Dynkin diagram
Cells 600 (3.3.3)
Faces 1200 {3}
Edges 720
Vertices 120
Vertex figure
icosahedron
Petrie polygon 30-gon
Coxeter group H4, [3,3,5]
Dual 120-cell
Properties convex, isogonal, isotoxal, isohedral
Uniform index 35

In geometry, the 600-cell (or hexacosichoron) is the convex regular 4-polytope, or polychoron, with Schläfli symbol {3,3,5}. Its boundary is composed of 600 tetrahedral cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. The edges form 72 flat regular decagons. Each vertex of the 600-cell is a vertex of six such decagons.

The mutual distances of the vertices, measured in degrees of arc on the circumscribed hypersphere, only have the values 36° = 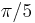\pi/5, 60°= 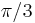\pi/3, 72° = 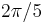2\pi/5, 90° = 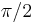\pi/2, 108° = 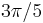3\pi/5, 120° = 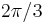2\pi/3, 144° = 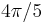4\pi/5, and 180° = \pi. Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron, at 60° and 120° the 20 vertices of a dodecahedron, at 72° and 108° again the 12 vertices of an icosahedron, at 90° the 30 vertices of an icosadodecahedron, and finally at 180° the antipodal vertex of V. References: S.L. van Oss (1899); F. Buekenhout and M. Parker (1998).

The 600-cell is regarded as the 4-dimensional analog of the icosahedron, since it has five tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex. It is also called a tetraplex (abbreviated from "tetrahedral complex") and polytetrahedron, being bounded by tetrahedral cells.

Its vertex figure is an icosahedron, and its dual polytope is the 120-cell.

Each cell touches, in some manner, 56 other cells. One cell contacts each of the four faces; two cells contact each of the six edges, but not a face; and ten cells contact each of the four vertices, but not a face or edge.

Contents

Coordinates

The vertices of a 600-cell centered at the origin of 4-space, with edges of length 1/φ (where φ = (1+√5)/2 is the golden ratio), can be given as follows: 16 vertices of the form:[1]

(±½,±½,±½,±½),

and 8 vertices obtained from

(0,0,0,±1)

by permuting coordinates. The remaining 96 vertices are obtained by taking even permutations of

½(±1,±φ,±1/φ,0).

Note that the first 16 vertices are the vertices of a tesseract, the second eight are the vertices of a 16-cell, and that all 24 vertices together are vertices of a 24-cell. The final 96 vertices are the vertices of a snub 24-cell, which can be found by partitioning each of the 96 edges of another 24-cell (dual to the first) in the golden ratio in a consistent manner.

When interpreted as quaternions, the 120 vertices of the 600-cell form a group under quaternionic multiplication. This group is often called the binary icosahedral group and denoted by 2I as it is the double cover of the ordinary icosahedral group I. It occurs twice in the rotational symmetry group RSG of the 600-cell as an invariant subgroup, namely as the subgroup 2IL of quaternion left-multiplications and as the subgroup 2IR of quaternion right-multiplications. Each rotational symmetry of the 600-cell is generated by specific elements of 2IL and 2IR; the pair of opposite elements generate the same element of RSG. The centre of RSG consists of the non-rotation Id and the central inversion -Id. We have the isomorphism RSG ≅ (2IL × 2IR) / {Id, -Id}. The order of RSG equals 120 × 120 / 2 = 7200.

The binary icosahedral group is isomorphic to SL(2,5).

The full symmetry group of the 600-cell is the Weyl group of H4. This is a group of order 14400. It consists of 7200 rotations and 7200 rotation-reflections. The rotations form an invariant subgroup of the full symmetry group. The rotational symmetry group was described by S.L. van Oss (1899); see References.

Visualization

The symmetries of the 3-D surface of the 600-cell are somewhat difficult to visualize due to both the large number of tetrahedral cells, and the fact that the tetrahedron has no opposing faces or vertices. One can start by realizing the 600-cell is the dual of the 120-cell.

Union of two tori

The 120-cell can be decomposed into two disjoint tori. Since it is the dual of the 600-cell, this same dual tori structure exists in the 600-cell, although it is somewhat more complex. The 10-cell geodesic path in the 120-cell corresponds to a 10-vertex decagon path in the 600-cell. Start by assembling five tetrahedrons around a common edge. This structure looks somewhat like an angular "flying saucer". Stack ten of these, vertex to vertex, "pancake" style. Fill in the annular ring between each "saucer" with 10 tetrahedrons forming an icosahedron. You can view this as five, vertex stacked, icosahedra, with the five extra annular ring gaps also filled in. You now have a torus consisting of 150 cells, ten edges long, with 100 exposed triangular faces. Stack another tetrahedron on each exposed face. This will give you a somewhat spiny torus of 250 cells with 50 raised vertices and 100 valley edges. Build a second identical torus of 250 cells that interlinks with the first. This accounts for 500 cells. These two tori mate together, leaving 100 tetrahedral voids that are filled with the remaining 100 tetrahedra.

Images

2D projections

Orthographic projections by Coxeter planes
H4 - F4

[30]
[20]
[12]
H3 A2 / B3 / D4 A3 / B2

[10]
[6]
[4]

3D projections

Vertex-first projection
This image shows a vertex-first perspective projection of the 600-cell into 3D. The 600-cell is scaled to a vertex-center radius of 1, and the 4D viewpoint is placed 5 units away. Then the following enhancements are applied:
  • The 20 tetrahedra meeting at the vertex closest to the 4D viewpoint are rendered in solid color. Their icosahedral arrangement is clearly shown.
  • The tetrahedra immediately adjoining these 20 cells are rendered in transparent yellow.
  • The remaining cells are rendered in edge-outline.
  • Cells facing away from the 4D viewpoint (those lying on the "far side" of the 600-cell) have been culled, to reduce visual clutter in the final image.
Cell-first projection
This image shows the 600-cell in cell-first perspective projection into 3D. Again, the 600-cell to a vertex-center radius of 1 and the 4D viewpoint is placed 5 units away. The following enhancements are then applied:
  • The nearest cell to the 4d viewpoint is rendered in solid color, lying at the center of the projection image.
  • The cells surrounding it (sharing at least 1 vertex) are rendered in transparent yellow.
  • The remaining cells are rendered in edge-outline.
  • Cells facing away from the 4D viewpoint have been culled for clarity.

This particular viewpoint shows a nice outline of 5 tetrahedra sharing an edge, towards the front of the 3D image.
Stereographic projection (on 3-sphere)
Cell-Centered
Simple Rotation
A 3D projection of a 600-cell performing a simple rotation.

Frame synchronized animated comparison of the 600 cell using orthogonal isometric (left) and perspective (right) projections.

Related polychora

The snub 24-cell may be obtained from the 600-cell by removing the vertices of an inscribed 24-cell and taking the convex hull of the remaining vertices. This process is a diminishing of the 600-cell.

The grand antiprism may be obtained by another diminishing of the 600-cell: removing 20 vertices that lie on two mutually orthogonal rings and taking the convex hull of the remaining vertices.

H4 family polytopes by name, Coxeter-Dynkin diagram, and Schläfli symbol
120-cell rectified
120-cell		 truncated
120-cell		 cantellated
120-cell		 runcinated
120-cell		 bitruncated
120-cell		 cantitruncated
120-cell		 runcitruncated
120-cell		 omnitruncated
120-cell
{5,3,3} t1{5,3,3} t0,1{5,3,3} t0,2{5,3,3} t0,3{5,3,3} t1,2{5,3,3} t0,1,2{5,3,3} t0,1,3{5,3,3} t0,1,2,3{5,3,3}
600-cell rectified
600-cell		 truncated
600-cell		 cantellated
600-cell		 runcinated
600-cell		 bitruncated
600-cell		 cantitruncated
600-cell		 runcitruncated
600-cell		 omnitruncated
600-cell
{3,3,5} t1{3,3,5} t0,1{3,3,5} t0,2{3,3,5} t0,3{3,3,5} t1,2{3,3,5} t0,1,2{3,3,5} t0,1,3{3,3,5} t0,1,2,3{3,3,5}

See also

Notes

  1. ^ Weisstein, Eric W., "600-cell" from MathWorld.

References

External links

5-cell 8-cell 16-cell 24-cell 120-cell 600-cell

{3,3,3}
pentachoron

{4,3,3}
tesseract

{3,3,4}
hexadecachoron

{3,4,3}
icositetrachoron

{5,3,3}
hecatonicosachoron

{3,3,5}
hexacosichoron