5-simplex honeycomb
| 5-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb |
| Family | Simplectic honeycomb |
| Schläfli symbol | {3[6]} |
| Coxeter–Dynkin diagrams | |
| 5-face types | {3,3,3,3} t1{3,3,3,3} t2{3,3,3,3} |
| 4-face types | {3,3,3} t1{3,3,3} |
| Cell types | {3,3} t1{3,3} |
| Face types | {3} |
| Vertex figure | t04{34} |
| Coxeter groups | 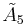 , [3[6]] , [3[6]] |
| Properties | vertex-transitive |
In five-dimensional Euclidean geometry, the 5-simplex honeycomb or hexateric honeycomb is a space-filling tessellation (or honeycomb or pentacomb). Each vertex is shared by 12 5-simplexes, 30 rectified 5-simplexes, and 20 birectified 5-simplexes. These facet types occur in proportions of 2:2:1 respectively in the whole honeycomb.
This vertex arrangement is called the A5 lattice or 5-simplex lattice. The 30 vertices of the stericated 5-simplex vertex figure represent the 30 roots of the 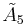 Coxeter group.[1]
Coxeter group.[1]
Contents |
Related polytopes and honeycombs
This honeycomb is one of 12 unique uniform honycombs[2] constructed by the 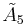 Coxeter group. The Coxeter–Dynkin diagrams of the other 11 are: , , , , , , , , , , .
Coxeter group. The Coxeter–Dynkin diagrams of the other 11 are: , , , , , , , , , , .
Projection by folding
The 5-simplex honeycomb can be projected into the 3-dimensional cubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:
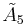 |
|
|---|---|
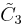 |
See also
- Regular and uniform honeycombs in 5-space:
Notes
- ^ http://www2.research.att.com/~njas/lattices/A5.html
- ^ [1], A000029 13-1 cases, skipping one with zero marks
References
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]