521 honeycomb
| E8 honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Family | k21 polytope |
| Schläfli symbol | {3,3,3,3,3,32,1} |
| Coxeter symbol | 521 |
| Coxeter-Dynkin diagram | |
| 8-faces | 511 {37} |
| 7-faces | {36} |
| 6-faces | {35} |
| 5-faces | {34} |
| 4-faces | {33} |
| Cells | {32} |
| Faces | {3} |
| Cell figure | 121 |
| Face figure | 221 |
| Edge figure | 321 |
| Vertex figure | 421 |
| Symmetry group | 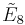 , [35,2,1] , [35,2,1] |
In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.
This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure[1] (Gosset regarded honeycombs in n dimensions as degenerate n+1 polytopes). In Coxeter's notation,[2] Gosset's honeycomb is denoted by 521.
Each vertex of the 521 honeycomb is surrounded by 2160 8-orthoplexes and 17280 8-simplices.
The vertex figure of Gosset's honeycomb is the semiregular 421 polytope. It is the final figure in the k21 family.
Its vertex arrangement is called the E8 lattice.[3]
This honeycomb is highly regular in the sense that its symmetry group (the affine E8 Weyl group) acts transitively on the k-faces for k ≤ 6. All of the k-faces for k ≤ 7 are simplices.
Contents |
Construction
It is created by a Wythoff construction upon a set of 9 hyperplane mirrors in 8-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram.
Removing the node on the end of the 2-length branch leaves the 8-orthoplex, 611.
Removing the node on the end of the 1-length branch leaves the 8-simplex.
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 421 polytope.
The edge figure is determined from the vertex figure by removing the ringed node and ringing the neighboring node. This makes the 321 polytope.
The face figure is determined from the edge figure by removing the ringed node and ringing the neighboring node. This makes the 221 polytope.
The cell figure is determined from the face figure by removing the ringed node and ringing the neighboring node. This makes the 121 polytope.
See also
Notes
- ^ Gosset, Thorold (1900). "On the regular and semi-regular figures in space of n dimensions". Messenger of Mathematics 29: 43–48.
- ^ Coxeter, H. S. M. (1973). Regular Polytopes ((3rd ed.) ed.). New York: Dover Publications. ISBN 0-486-61480-8.
- ^ http://www2.research.att.com/~njas/lattices/E8.html
References
- Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Coxeter Regular Polytopes (1963), Macmillian Company
- Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]