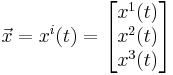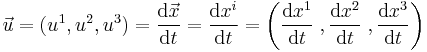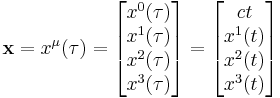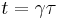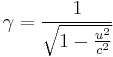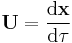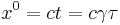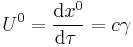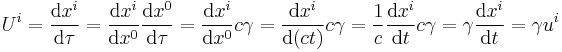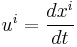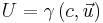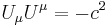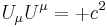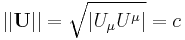Four-velocity

In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector (vector in four-dimensional spacetime) that replaces classical velocity (a three-dimensional vector). It is chosen in such a way that the velocity of light is a constant as measured in every inertial reference frame.

In relativity theory events are described in time and space, together forming four-dimensional spacetime. The history of an object traces a curve in spacetime, parametrized by a curve parameter, the proper time of the object. This curve is called its world line. The four-velocity is the rate of change of both time and space coordinates with respect to the proper time of the object. The four-velocity is a tangent vector to the world line.

For comparison: in classical mechanics events are described by their (three-dimensional) position at each moment in time. The path of an object is a curve in three-dimensional space, parametrized by the time. The classical velocity is the rate of change of the space coordinates of the object with respect to the time. The classical velocity of an object is a tangent vector to its path.

The length of the four-velocity (in the sense of the metric used in special relativity) is always equal to c (it is a normalized vector). For an object at rest (with respect to the coordinate system) its four-velocity points in the direction of the time coordinate.

1 Classical mechanics
2 Theory of relativity
3 Interpretation
4 See also
5 References

Classical mechanics

In classical mechanics the path of an object in three-dimensional space is determined by three coordinate functions 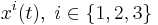$x^i(t),\; i \in \{1,2,3\}$ as a function of (absolute) time t:

$\vec{x} = x^i(t) = \begin{bmatrix} x^1(t) \\ x^2(t) \\ x^3(t) \\ \end{bmatrix}$

where the 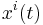$x^i(t)$ denote the three spatial positions of the object at time t.

The components of the classical velocity 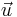${\vec{u}}$ at a point p (tangent to the curve) are

${\vec{u}} = (u^1,u^2,u^3) = {\mathrm{d} \vec{x} \over \mathrm{d}t} = {\mathrm{d}x^i \over \mathrm{d}t} = \left(\frac{\mathrm{d}x^1}{\mathrm{d}t}\;,\frac{\mathrm{d}x^2}{\mathrm{d}t}\;,\frac{\mathrm{d}x^3}{\mathrm{d}t}\right)$

where the derivatives are taken at the point p. So they are the difference in two nearby positions 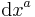$\mathrm{d}x^a$ divided by the time interval $\mathrm{d}t$ .

Theory of relativity

In Einstein's theory of relativity, the path of an object moving relative to a particular frame of reference is defined by four coordinate functions 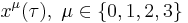$x^{\mu}(\tau),\; \mu \in \{0,1,2,3\}$ (where 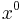$x^{0}$ denotes the time coordinate multiplied by c), each function depending on one parameter $\tau$ , called its proper time.

$\mathbf{x} = x^{\mu}(\tau) = \begin{bmatrix} x^0(\tau)\\ x^1(\tau) \\ x^2(\tau) \\ x^3(\tau) \\ \end{bmatrix} = \begin{bmatrix} ct \\ x^1(t) \\ x^2(t) \\ x^3(t) \\ \end{bmatrix}$

Time dilation

From time dilation, we know that

$t = \gamma \tau \,$

where $\gamma$ is the Lorentz factor, which is defined as:

$\gamma = \frac{1}{\sqrt{1-\frac{u^2}{c^2}}}$

and u is the Euclidean norm of the classical velocity vector 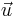$\vec{u}$ :

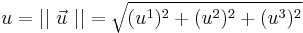$u = || \ \vec{u} \ || = \sqrt{ (u^1)^2 %2B (u^2)^2 %2B (u^3)^2}$ .

Definition of the four-velocity

The four-velocity is the tangent four-vector of a world line. The four velocity of world line 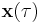$\mathbf{x}(\tau)$ is defined as:

$\mathbf{U} = \frac{\mathrm{d}\mathbf{x}}{\mathrm{d} \tau}$

where

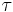$\tau \,$ is the proper time.

Components of the four-velocity

The relationship between the time t and the coordinate time 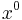$x^0$ is given by

$x^0 = ct = c \gamma \tau \,$

Taking the derivative with respect to the proper time 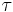$\tau \,$ , we find the 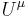$U^\mu \,$ velocity component for μ = 0:

$U^0 = \frac{\mathrm{d}x^0}{\mathrm{d}\tau\;} = c \gamma$

Using the chain rule, for 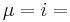$\mu = i =$ 1, 2, 3, we have

$U^i = \frac{\mathrm{d}x^i}{\mathrm{d}\tau} = \frac{\mathrm{d}x^i}{\mathrm{d}x^0} \frac{\mathrm{d}x^0}{\mathrm{d}\tau} = \frac{\mathrm{d}x^i}{\mathrm{d}x^0} c\gamma = \frac{\mathrm{d}x^i}{\mathrm{d}(ct)} c\gamma = {1 \over c} \frac{\mathrm{d}x^i}{\mathrm{d}t} c\gamma = \gamma \frac{\mathrm{d}x^i}{\mathrm{d}t} = \gamma u^i$

where we have used the relationship

$u^i = {dx^i \over dt }$

from classical mechanics. Thus, we find for the four-velocity $U$ :

$U = \gamma \left( c, \vec{u} \right)$

In terms of the yardsticks (and synchronized clocks) associated with a particular slice of flat spacetime, the three spacelike components of 4-velocity define a traveling object's proper velocity 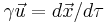$\gamma \vec{u} = d\vec{x}/d\tau$ i.e. the rate at which distance is covered in the reference map-frame per unit proper time elapsed on clocks traveling with the object.

Interpretation

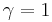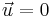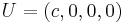For a rest frame, of course, $\gamma = 1$ and $\vec{u} = 0$ , hence $U = (c,0,0,0) \,$ thus justifying the statement about traveling in the time direction.

In every frame of reference, in both special and general relativity, we have

$U_\mu U^\mu = -c^2 \,$

if the signature of the metric is (-1,1,1,1).

Otherwise, if the signature is taken to be (1,-1,-1,-1), we have

$U_\mu U^\mu = %2Bc^2 \,$

However, in both cases:

$|| \mathbf{U} || = \sqrt{ | U_\mu U^\mu | } = c$

In other words, the norm or magnitude of the four-velocity of a rest-massive object is always exactly equal to the speed of light. Thus all rest-massive objects can be thought of as moving through spacetime at the speed of light.

This provides a way of understanding time-dilation. As an object like a rocket accelerates from our perspective, it moves not only faster through space, but also faster through time in order to keep the magnitude of the four-velocity constant. As the speed through time $dt/dτ$ increases, the rate of aging $dτ/dt$ decreases. Thus to an observer, a clock on the rocket moves slower, as do the clocks in any reference frame that is not comoving with them.^[1]

The four-velocity defined above via the rest frame of an object does not exist for rest-massless objects such as light, since light does not have a Lorentz inertial rest frame. However, the four-velocity can also be thought of as the tangent vector to an object's spacetime path. With this definition, the 4-velocity of light has zero spacetime "length". Formally, this is equivalent to a photon's path being a null geodesic. Heuristically, a photon always travels "equally" in coordinate space and time, its path being the diagonal in a spacetime diagram in which a particular Lorentz inertial coordinate system has been chosen. The two pictures are equivalent, since the diagonal is a null geodesic.

References

^ Grøn, Øyvind; Næss, Arne (2011), Einstein's Theory: A Rigorous Introduction for the Mathematically Untrained, Springer, pp. 202–203, doi:10.1007/978-1-4614-0706-5, ISBN 978-1-4614-0705-8

Einstein, Albert; translated by Robert W. Lawson (1920). Relativity: The Special and General Theory. New York: Original: Henry Holt, 1920; Reprinted: Prometheus Books, 1995.
Rindler, Wolfgang (1991). Introduction to Special Relativity (2nd). Oxford: Oxford University Press. ISBN 0-19-853952-5.