142857 (number)
142857 is the six repeating digits of 1/7, 0.142857, and is the best-known cyclic number in base 10.[1][2][3][4] If it is multiplied by 2, 3, 4, 5, or 6, the answer will be a cyclic permutation of itself, and will correspond to the repeating digits of 2/7, 3/7, 4/7, 5/7, or 6/7, respectively.
Contents |
Calculations
| List of numbers 100000 142857 1000000 |
|
|---|---|
| Cardinal | One hundred forty-two thousand, eight hundred fifty-seven |
| Ordinal | 142,857th |
| Roman numeral | CXLMMDCCCLVII |
| Factorization | 142857 = 33 • 11 • 13 • 37 |
| Binary | 100010111000001001 |
| Hexadecimal | 22E09 |
| Octal | 427011 |
- 1 × 142,857 = 142,857
- 2 × 142,857 = 285,714
- 3 × 142,857 = 428,571
- 4 × 142,857 = 571,428
- 5 × 142,857 = 714,285
- 6 × 142,857 = 857,142
- 7 × 142,857 = 999,999
If you multiply by an integer greater than 7, there is a simple process to get to a cyclic permutation of 142857. By adding the first six digits (ones through hundred thousands) to the remaining digits and repeating this process until you have only the six digits left, it will result in a cyclic permutation of 142857
- 142857 × 8 = 1142856
- 1 + 142856 = 142857
- 142857 × 815 = 116428455
- 116 + 428455 = 428571
- 1428572 = 142857 × 142857 = 20408122449
- 20408 + 122449 = 142857
Multiplying by a multiple of 7 will result in 999999 through this process
- 142857 × 74 = 342999657
- 342 + 999657 = 999999
If you square the last three digits and subtract the square of the first three digits, you also get back a cyclic permutation of the number.
- 8572 = 734449
- 1422 = 20164
- 734449 − 20164 = 714285
It is the repeating part in the decimal expansion of the rational number 1/7 = 0.142857. Thus, multiples of 1/7 are simply repeated copies of the corresponding multiples of 142857:
- 1 ÷ 7 = 0.142857
- 2 ÷ 7 = 0.285714
- 3 ÷ 7 = 0.428571
- 4 ÷ 7 = 0.571428
- 5 ÷ 7 = 0.714285
- 6 ÷ 7 = 0.857142
- 7 ÷ 7 = 0.999999
- 8 ÷ 7 = 1.142857
- 9 ÷ 7 = 1.285714
- …
In base 10, 142,857 is a Harshad number and a Kaprekar number.
1/7 as an infinite sum
There is an interesting pattern of doubling, shifting and addition that gives 1/7.
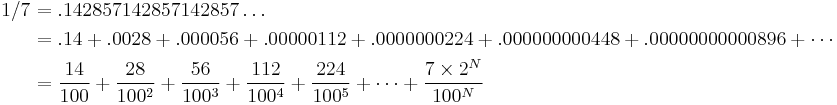
Each term is double the prior term shifted two places to the right.
22/7 as π
This ancient approximation to π, 22 ÷ 7 = 3.142857, has been associated with Jewish mysticism. In particular, it is known in certain circles of Kabbalists such as the "Mediogegnians", that the twenty two characters of the Hebrew language represent a complete circumference that when divided by seven (the sacred number of cycles) produces the Kabbalistic π, also known within this circle of practitioners as the "perfect π".
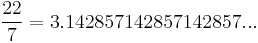
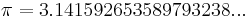
The difference between these two numbers is
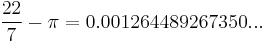
Other bases
In some other bases, six-digit numbers with similar properties exist, given by (base6 − 1)/7. E.g. in base 12 it is 186A35 and base 24 3A6LDH.
Connection to the enneagram
142857 is the number used to construct the Enneagram, a sacred symbol of the Gurdjieff Work, that is used to explain and visualize the dynamics of the interaction between the two great laws of the Universe (according to Gurdjieff), the Law of Three and the Law of Seven. The movement of the numbers of 142857 divided by 1/7,2/7. etc., and the subsequent movement of the Enneagram, are portrayed in Gurdjieffs Sacred Dances, known as the Movements.
References
- ^ "Cyclic number", The Internet Encyclopedia of Science
- ^ Michael W. Ecker, "The Alluring Lore of Cyclic Numbers", The Two-Year College Mathematics Journal, Vol.14, No.2 (March 1983), pp.105-109
- ^ Cyclic number, PlanetMath
- ^ Hogan, Kathryn (August 2005). "Go figure (cyclic numbers)". Australian Doctor. Archived from the original on 24 December 2007. http://web.archive.org/web/20071224191059/http://findarticles.com/p/articles/mi_hb4870/is_200508/ai_n17913296.
- Leslie, John. "The Philosophy of Arithmetic: Exhibiting a Progressive View of the Theory and Practice of ....", Longman, Hurst, Rees, Orme, and Brown, 1820, ISBN 1-4020-1546-1
- Wells, D. The Penguin Dictionary of Curious and Interesting Numbers Revised Edition. London: Penguin Group. (1997): 171 - 175