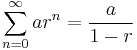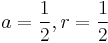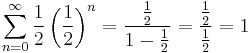1/2 + 1/4 + 1/8 + 1/16 + · · ·
In mathematics, the infinite series 1/2 + 1/4 + 1/8 + 1/16 + · · · is an elementary example of a series that converges absolutely.
Its sum is
By factoring 1/2 out of every term in this series this infinite sum can be rewritten as:
This is a special case of the geometric series:
where a is the common ratio (gcd) between all terms
These series are known to converge to a finite point given the following condition:
If a series can be written in the general form stated above and satisfies the preceding condition the series converges to a computable value at infinity given by the following formula:
where a is the common ratio
Considering our special case where:
We yield the following result:
History
This series was used as a representation of one of Zeno's paradoxes.[1] The parts of the Eye of Horus represent the first six summands of the series.
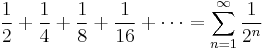
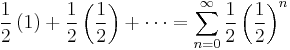
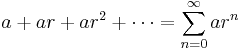
![r \in \ ]-1,1[](/2012-wikipedia_en_all_nopic_01_2012/I/58e1a3b43c58043e0429cfd1112392fc.png)