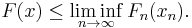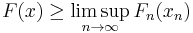Γ-convergence

In the calculus of variations, Γ-convergence (Gamma-convergence) is a notion of convergence for functionals. It was introduced by Ennio de Giorgi.

Definition

Let X be a topological space and F_n:X→[0,∞] a sequence of functionals on X. Then F_n are said to Γ-converge to the Γ-limit F:X→[0,∞] if the following two conditions hold:

• Lower bound inequality: For every sequence x_n in X such that x_n→x as n→∞,

• Upper bound inequality: For every x∈X, there is a sequence x_n converging to x such that

The first condition means that F provides an asymptotic common lower bound for the F_n. The second condition means that this lower bound is optimal.

Properties

• Minimizers converge to minimizers: If F_n Γ-converge to F, and x_n is a minimizer for F_n, then every cluster point of the sequence x_n is a minimizer of F.
• Γ-limits are always lower semicontinuous.
• Γ-convergence is stable under continuous perturbations: If F_n Γ-converges to F and G:X→[0,∞] is continuous, then F_n+G will Γ-converge to F+G.
• A constant sequence of functionals F_n=F does not necessarily Γ-converge to F, but to the relaxation of F, the largest lower semicontinuous functional below F.

Applications

An important use for Γ-convergence is in homogenization theory. It can also be used to rigorously justify the passage from discrete to continuum theories for materials, e.g. in elasticity theory.

See also

• Mosco convergence

References

• A. Braides: Γ-convergence for beginners. Oxford University Press, 2002.
• G. Dal Maso: An introduction to Γ-convergence. Birkhäuser, Basel 1993.