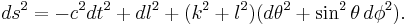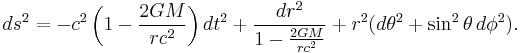Wormhole

Analogy to a wormhole in a curved 2-D space (see Embedding Diagram)
An artist's impression of a wormhole from an observer's perspective, crossing the event horizon of a Schwarzschild wormhole which bridges two different universes. The observer originates from the right, and another universe becomes visible in the center of the wormhole’s shadow once the horizon is crossed, the observer seeing light that has fallen into the black hole interior region from the other universe; however, this other universe is unreachable in the case of a Schwarzschild wormhole, as the bridge always collapses before the observer has time to cross it, and everything that has fallen through the event horizon of either universe is inevitably crushed in the black hole singularity. See White Holes and Wormholes for a technical discussion and animation of what an observer sees when falling into a Schwarzschild wormhole (also see Approaching the Black Hole from the same site for background, and perhaps also the more detailed renderings at Journey into a Schwarzschild black hole)
Image of a traversable wormhole which connects the place in front of the physical institutes of Tübingen university with the sand dunes near Boulogne sur Mer in the north of France. The image is calculated with 4D raytracing in a Morris-Thorne wormhole metric. Other computer-rendered images and animations of traversable wormholes can be seen on this page and this one.

In physics and fiction, a wormhole is a hypothetical topological feature of spacetime that would be, fundamentally, a "shortcut" through spacetime. For a simple visual explanation of a wormhole, consider spacetime visualized as a two-dimensional (2-D) surface (see illustration, right). If this surface is "folded" along a (non-existent) third dimension, it allows one to picture a wormhole "bridge". (Please note, though, that this image is merely a visualization displayed to convey an essentially unvisualisable structure existing in 4 or more dimensions. The parts of the wormhole could be higher-dimensional analogues for the parts of the curved 2D surface; for example, instead of mouths which are circular holes in a 2D plane, a real wormhole's mouths could be spheres in 3D space.) A wormhole is, in theory, much like a tunnel with two ends each in separate points in spacetime.

There is no observational evidence for wormholes, but on a theoretical level there are valid solutions to the equations of the theory of general relativity which contain wormholes. The first type of wormhole solution discovered was the Schwarzschild wormhole which would be present in the Schwarzschild metric describing an eternal black hole, but it was found that this type of wormhole would collapse too quickly for anything to cross from one end to the other. Wormholes which could actually be crossed, known as traversable wormholes, would only be possible if exotic matter with negative energy density could be used to stabilize them (many physicists such as Stephen Hawking[1], Kip Thorne[2], and others[3][4][5] believe that the Casimir effect is evidence that negative energy densities are possible in nature). Physicists have also not found any natural process which would be predicted to form a wormhole naturally in the context of general relativity, although the quantum foam hypothesis is sometimes used to suggest that tiny wormholes might appear and disappear spontaneously at the Planck scale.[6][7] It has also been proposed that if a tiny wormhole held open by a negative-mass cosmic string had appeared around the time of the Big Bang, it could have been inflated to macroscopic size by cosmic inflation.[8]

The American theoretical physicist John Archibald Wheeler coined the term wormhole in 1957; however, in 1921, the German mathematician Hermann Weyl already had proposed the wormhole theory, in connection with mass analysis of electromagnetic field energy.[9]

This analysis forces one to consider situations...where there is a net flux of lines of force, through what topologists would call "a handle" of the multiply-connected space, and what physicists might perhaps be excused for more vividly terming a "wormhole".
—John Wheeler in Annals of Physics

Contents

Definition

The basic notion of an intra-universe wormhole is that it is a compact region of spacetime whose boundary is topologically trivial but whose interior is not simply connected. Formalizing this idea leads to definitions such as the following, taken from Matt Visser's Lorentzian Wormholes.

If a Minkowski spacetime contains a compact region Ω, and if the topology of Ω is of the form Ω ~ R x Σ, where Σ is a three-manifold of the nontrivial topology, whose boundary has topology of the form dΣ ~ S2, and if, furthermore, the hypersurfaces Σ are all spacelike, then the region Ω contains a quasipermanent intra-universe wormhole.

Characterizing inter-universe wormholes is more difficult. For example, one can imagine a 'baby' universe connected to its 'parent' by a narrow 'umbilicus'. One might like to regard the umbilicus as the throat of a wormhole, but the spacetime is simply connected.

Schwarzschild wormholes

Embedded diagram of a Schwarzschild wormhole.

Lorentzian wormholes known as Schwarzschild wormholes or Einstein-Rosen bridges are bridges between areas of space that can be modeled as vacuum solutions to the Einstein field equations, and which are now understood to be intrinsic parts of the maximally extended version of the Schwarzschild metric describing an eternal black hole with no charge and no rotation. Here, "maximally extended" refers to the idea that the spacetime should not have any "edges": for any possible trajectory of a free-falling particle (following a geodesic) in the spacetime, it should be possible to continue this path arbitrarily far into the particle's future or past, unless the trajectory hits a gravitational singularity like the one at the center of the black hole's interior. In order to satisfy this requirement, it turns out that in addition to the black hole interior region which particles enter when they fall through the event horizon from the outside, there must be a separate white hole interior region which allows us to extrapolate the trajectories of particles which an outside observer sees rising up away from the event horizon. And just as there are two separate interior regions of the maximally extended spacetime, there are also two separate exterior regions, sometimes called two different "universes", with the second universe allowing us to extrapolate some possible particle trajectories in the two interior regions. This means that the interior black hole region can contain a mix of particles that fell in from either universe (and thus an observer who fell in from one universe might be able to see light that fell in from the other one), and likewise particles from the interior white hole region can escape into either universe. All four regions can be seen in a spacetime diagram which uses Kruskal–Szekeres coordinates, as discussed and illustrated on the page White Holes and Wormholes.

In this spacetime, it is possible to come up with coordinate systems such that if you pick a hypersurface of constant time (a set of points that all have the same time coordinate, such that every point on the surface has a space-like separation, giving what is called a 'space-like surface') and draw an "embedding diagram" depicting the curvature of space at that time (see the discussion of embedding diagrams on this page), the embedding diagram will look like a tube connecting the two exterior regions, known as an "Einstein-Rosen bridge". For example, see the diagrams on this page which show the maximally extended Schwarzschild solution in Kruskal–Szekeres coordinates along with white hypersurfaces of constant time drawn on (time in some other coordinate system besides Kruskal–Szekeres coordinates, since a hypersurface of constant Kruskal–Szekeres time would just look like a horizontal line when drawn in a Kruskal–Szekeres diagram), and the corresponding embedding diagram for that hypersurface. Note that the Schwarzschild metric describes an idealized black hole that exists eternally from the perspective of external observers; a more realistic black hole that forms at some particular time from a collapsing star would require a different metric. When the infalling stellar matter is added to a diagram of a black hole's history, it removes the part of the diagram corresponding to the white hole interior region, along with the part of the diagram corresponding to the other universe.[10]

The Einstein-Rosen bridge was discovered by Albert Einstein and his colleague Nathan Rosen, who first published the result in 1935. However, in 1962 John A. Wheeler and Robert W. Fuller published a paper showing that this type of wormhole is unstable, and that it will pinch off too quickly for light (or any particle moving slower than light) that falls in from one exterior region to make it to the other exterior region.

Before the stability problems of Schwarzschild wormholes were apparent, it was proposed that quasars were white holes forming the ends of wormholes of this type.

While Schwarzschild wormholes are not traversable, their existence inspired Kip Thorne to imagine traversable wormholes created by holding the 'throat' of a Schwarzschild wormhole open with exotic matter (material that has negative mass/energy).

Traversable wormholes

Lorentzian traversable wormholes would allow travel from one part of the universe to another part of that same universe very quickly or would allow travel from one universe to another. The possibility of traversable wormholes in general relativity was first demonstrated by Kip Thorne and his graduate student Mike Morris in a 1988 paper; for this reason, the type of traversable wormhole they proposed, held open by a spherical shell of exotic matter, is referred to as a Morris-Thorne wormhole. Later, other types of traversable wormholes were discovered as allowable solutions to the equations of general relativity, including a variety analyzed in a 1989 paper by Matt Visser, in which a path through the wormhole can be made in which the traversing path does not pass through a region of exotic matter. However in the pure Gauss-Bonnet theory (a modification to general relativity involving extra spatial dimensions which is sometimes studied in the context of brane cosmology) exotic matter is not needed in order for wormholes to exist- they can exist even with no matter.[11] A type held open by negative mass cosmic strings was put forth by Visser in collaboration with Cramer et al.,[8] in which it was proposed that such wormholes could have been naturally created in the early universe.

Wormholes connect two points in spacetime, which means that they would in principle allow travel in time, as well as in space. In 1988, Morris, Thorne and Yurtsever worked out explicitly how to convert a wormhole traversing space into one traversing time.[12] However, according to general relativity it would not be possible to use a wormhole to travel back to a time earlier than when the wormhole was first converted into a time machine by accelerating one of its two mouths.[13]

Raychaudhuri's theorem and exotic matter

To see why exotic matter is required, consider an incoming light front traveling along geodesics, which then crosses the wormhole and re-expands on the other side. The expansion goes from negative to positive. As the wormhole neck is of finite size, we would not expect caustics to develop, at least within the vicinity of the neck. According to the optical Raychaudhuri's theorem, this requires a violation of the averaged null energy condition. Quantum effects such as the Casimir effect cannot violate the averaged null energy condition in any neighborhood of space with zero curvature[14], but calculations in semiclassical gravity suggest that quantum effects may be able to violate this condition in curved spacetime.[15] Even if they can, it may be that quantum effects cannot violate a weaker condition known as the "achronal averaged null energy condition", and that this could rule out the possibility of traversable wormholes.[16]

Faster-than-light travel

The impossibility of faster-than-light relative speed only applies locally. Wormholes allow superluminal (faster-than-light) travel by ensuring that the speed of light is not exceeded locally at any time. While traveling through a wormhole, subluminal (slower-than-light) speeds are used. If two points are connected by a wormhole, the time taken to traverse it would be less than the time it would take a light beam to make the journey if it took a path through the space outside the wormhole. However, a light beam traveling through the wormhole would always beat the traveler. As an analogy, running around to the opposite side of a mountain at maximum speed may take longer than walking through a tunnel crossing it.

Time travel

The theory of general relativity predicts that if traversable wormholes exist, they could allow time travel.[12] This would be accomplished by accelerating one end of the wormhole to a high velocity relative to the other, and then sometime later bringing it back; relativistic time dilation would result in the accelerated wormhole mouth aging less than the stationary one as seen by an external observer, similar to what is seen in the twin paradox. However, time connects differently through the wormhole than outside it, so that synchronized clocks at each mouth will remain synchronized to someone traveling through the wormhole itself, no matter how the mouths move around.[17] This means that anything which entered the accelerated wormhole mouth would exit the stationary one at a point in time prior to its entry.

For example, consider two clocks at both mouths both showing the date as 2000. After being taken on a trip at relativistic velocities, the accelerated mouth is brought back to the same region as the stationary mouth with the accelerated mouth's clock reading 2005 while the stationary mouth's clock read 2010. A traveller who entered the accelerated mouth at this moment would exit the stationary mouth when its clock also read 2005, in the same region but now five years in the past. Such a configuration of wormholes would allow for a particle's world line to form a closed loop in spacetime, known as a closed timelike curve.

It is thought that it may not be possible to convert a wormhole into a time machine in this manner; the predictions are made in the context of general relativity, but general relativity does not include quantum effects. Some analyses using the semiclassical approach to incorporating quantum effects into general relativity indicate that a feedback loop of virtual particles would circulate through the wormhole with ever-increasing intensity, destroying it before any information could be passed through it, in keeping with the chronology protection conjecture. This has been called into question by the suggestion that radiation would disperse after traveling through the wormhole, therefore preventing infinite accumulation. The debate on this matter is described by Kip S. Thorne in the book Black Holes and Time Warps, and a more technical discussion can be found in The quantum physics of chronology protection by Matt Visser. There is also the Roman ring, which is a configuration of more than one wormhole. This ring seems to allow a closed time loop with stable wormholes when analyzed using semiclassical gravity, although without a full theory of quantum gravity it is uncertain whether the semiclassical approach is reliable in this case.

Metrics

Theories of wormhole metrics describe the spacetime geometry of a wormhole and serve as theoretical models for time travel. An example of a (traversable) wormhole metric is the following:

ds^2= - c^2 dt^2 + dl^2 + (k^2 + l^2)(d \theta^2 + \sin^2 \theta \, d\phi^2).

One type of non-traversable wormhole metric is the Schwarzschild solution:

ds^2= - c^2 \left(1 - \frac{2GM}{rc^2}\right)dt^2 + \frac{dr^2}{1 - \frac{2GM}{rc^2}} + r^2(d \theta^2 + \sin^2 \theta \, d\phi^2).

In fiction

Wormholes are a common element in science fiction as they allow interstellar (and sometimes interuniversal) travel within human timescales.

Wormholes also play pivotal roles in science fiction where faster-than-light travel is possible though limited, allowing connections between regions that would be otherwise unreachable within conventional timelines. Several examples appear in the Star Trek franchise, using wormholes, artificial wormholes and transwarp conduits, allowing ships to move nearly instantaneously to any part of the galaxy in which an exit aperture exists. Other fictional universes using or referring to wormholes are:

See also

Notes

  1. ↑ http://www.hawking.org.uk/index.php/lectures/63
  2. ↑ M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition, Physical Review, 61, 13, September 1988, pp. 1446 - 1449
  3. ↑ http://arxiv.org/pdf/quant-ph/0204125
  4. ↑ http://arxiv.org/pdf/gr-qc/9410043
  5. ↑ http://arxiv.org/pdf/gr-qc/9805003
  6. ↑ Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. pp. 494–496. ISBN 0-393-31276-3. 
  7. ↑ Ian H., Redmount; Wai-Mo Suen (1994). "Quantum Dynamics of Lorentzian Spacetime Foam". Physical Review D 49: 5199. doi:10.1103/PhysRevD.49.5199.  arXiv:gr-qc/9309017
  8. ↑ 8.0 8.1 John G. Cramer, Robert L. Forward, Michael S. Morris, Matt Visser, Gregory Benford, and Geoffrey A. Landis, "Natural Wormholes as Gravitational Lenses," Phys. Rev. D51 (1995) 3117-3120
  9. ↑ Coleman, Korte, Hermann Weyl's Raum - Zeit - Materie and a General Introduction to His Scientific Work, p. 199
  10. ↑ http://casa.colorado.edu/~ajsh/collapse.html#kruskal
  11. ↑ gr-qc/0701152 (January 2007) `Mass without mass' from thin shells in Gauss-Bonnet gravity Elias Gravanis and Steven Willison
  12. ↑ 12.0 12.1 M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition, Physical Review, 61, 13, September 1988, pp. 1446 - 1449
  13. ↑ Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. pp. 504. ISBN 0-393-31276-3. 
  14. ↑ Fewster, Christopher J.; Ken D. Olum, Michael J. Pfenning (10 January 2007). "Averaged null energy condition in spacetimes with boundaries". Physical Review D 75 (2): 025007. doi:10.1103/PhysRevD.75.025007. http://arxiv.org/abs/gr-qc/0609007. 
  15. ↑ Visser, Matt (15 October 1996). "Gravitational vacuum polarization. II. Energy conditions in the Boulware vacuum". Physical Review D 54 (8): 5116. doi:10.1103/PhysRevD.54.5116. http://arxiv.org/abs/gr-qc/9604008. 
  16. ↑ Graham, Noah; Ken D. Olum (4 September 2007). "Achronal averaged null energy condition". Physical Review D 76 (6): 064001. doi:10.1103/PhysRevD.76.064001. http://arxiv.org/abs/0705.3193. 
  17. ↑ Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. pp. 502. ISBN 0-393-31276-3. 

References

External links