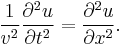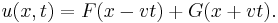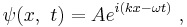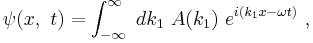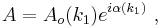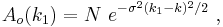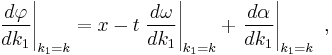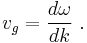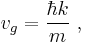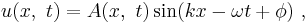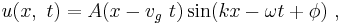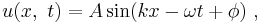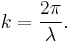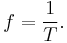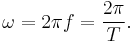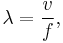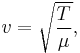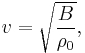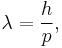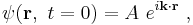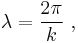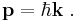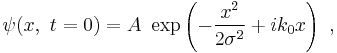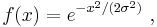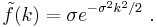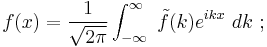Wave

Amplitude modulation and frequency modulation of a "Carrier wave" by a signal

In mathematics and science, a wave is a disturbance that travels through space and time, usually by the transfer of energy. Waves are described by a wave equation that can take on many forms depending on the type of wave. A mechanical wave is a wave that propagates through a medium owing to restoring forces resulting from its deformation. For example, sound waves propagate via air molecules bumping into their neighbors. This transfers some energy to these neighbors, which will cause a cascade of collisions between neighbouring molecules. When air molecules collide with their neighbors, they also bounce away from them (restoring force). This keeps the molecules from actually traveling with the wave.

Waves travel and transfer energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass transport. They consist instead of oscillations or vibrations around almost fixed locations. For example, a cork on rippling water will bob up and down while staying in about the same place while the wave itself moves onwards. Waves carry energy but not mass because even as a wave travels outward from the center (carrying energy of motion), the medium itself does not flow with it.

There are also waves capable of travelling through a vacuum, e.g. electromagnetic radiation (including visible light, ultraviolet radiation, infrared radiation, gamma rays, X-rays, and radio waves). They consist of period oscillations in electrical and magnetic properties that grow, reach a peak, and diminish to zero in a periodic fashion.

Researchers believe that gravitational waves travel through space, although gravitational waves have never been directly detected. (See gravitational radiation.)

General features

A single, all-encompassing definition for the term wave is not straightforward. A vibration can be defined as a back-and-forth motion around a reference value. However, a vibration is not necessarily a wave. Defining the necessary and sufficient characteristics that qualify a phenomenon to be called a wave is flexible.

The term wave is often understood intuitively as the transport of disturbances in space, these disturbances generally not associated with motion of the medium occupying this space as a whole. In a wave, the energy of a vibration is moving away from the source in the form of a disturbance within the surrounding medium (Hall 1980, p. 8). However, this notion is problematic for a standing wave (for example, a wave on a string), where energy is moving in both directions equally, or for electromagnetic / light waves in a vacuum, where the concept of medium does not apply. There are water waves in the ocean; light waves from the sun; microwaves inside the microwave oven; radio waves transmitted to the radio; and sound waves from the radio, telephone, and person.

It may be seen that the description of waves is accompanied by a heavy reliance on physical origin when describing any specific instance of a wave process. For example, acoustics is distinguished from optics in that sound waves are related to a mechanical rather than an electromagnetic wave-like transfer / transformation of vibratory energy. Concepts such as mass, momentum, inertia, or elasticity, become therefore crucial in describing acoustic (as distinct from optic) wave processes. This difference in origin introduces certain wave characteristics particular to the properties of the medium involved (for example, in the case of air: vortices, radiation pressure, shock waves, etc., in the case of solids: Rayleigh waves, dispersion, etc., and so on).

Other properties, however, although they are usually described in an origin-specific manner, may be generalized to all waves. For such reasons, wave theory represents a particular branch of physics that is concerned with the properties of wave processes independently from their physical origin.^[1] For example, based on the mechanical origin of acoustic waves there can be a moving disturbance in space–time if and only if the medium involved is neither infinitely stiff nor infinitely pliable. If all the parts making up a medium were rigidly bound, then they would all vibrate as one, with no delay in the transmission of the vibration and therefore no wave motion. On the other hand, if all the parts were independent, then there would not be any transmission of the vibration and again, no wave motion. Although the above statements are meaningless in the case of waves that do not require a medium, they reveal a characteristic that is relevant to all waves regardless of origin: within a wave, the phase of a vibration (that is, its position within the vibration cycle) is different for adjacent points in space because the vibration reaches these points at different times.

Similarly, wave processes revealed from the study of waves other than sound waves can be significant to the understanding of sound phenomena. A relevant example is Thomas Young's principle of interference (Young, 1802, in Hunt 1992, p. 132). This principle was first introduced in Young's study of light and, within some specific contexts (for example, scattering of sound by sound), is still a researched area in the study of sound.

Mathematical description

Wave equation

Main articles: Wave equation and D'Alembert's formula

For a wave moving in one dimension travelling along the x-axis whose shape stays the same, whether or not it be a pulse, the wave function takes one of the forms,

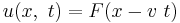$u(x, \ t) = F(x - v \ t)$ (travelling to the right)

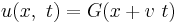$u(x, \ t) = G(x + v \ t)$ (travelling to the left)

It can be shown that both these wave functions satisfy the wave equation,

$\frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}=\frac{\partial^2 u}{\partial x^2}. \,$

The wave equation is a partial differential equation that describes the evolution of a wave over time in a medium where the wave propagates at the same speed independent of wavelength (no dispersion), and independent of amplitude (linear media, not nonlinear).^[2] General solutions are based upon Duhamel's principle.^[3]

In particular, consider the wave equation in one dimension, for example, as applied to a string. Suppose a one-dimensional wave is traveling along the x axis with velocity 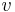$v$ and amplitude $u$ (which generally depends on both x and t), the wave equation is

The velocity v will depend on the medium through which the wave is moving.

The general solution for the wave equation in one dimension was given by d'Alembert; it is known as d'Alembert's formula:^[4]

$u(x,t)=F(x-vt)+G(x+vt). \,$

This formula represents two shapes traveling through the medium in opposite directions; F in the positive x direction, and G in the negative x direction, of arbitrary functional shapes F and G.

Wavelength λ, can be measured between any two corresponding points.

Wave forms

Sine, square, triangle and sawtooth waveforms.

The form of the forward propagating wave F in d'Alembert's formula involves the argument x − vt. Constant values of this argument correspond to constant values of F, and these constant values occur if x increases at the same rate that vt increases. That is, the wave shaped like the function F will move in the positive x-direction at velocity v (and G will propagate at the same speed in the negative x-direction).^[5]

In the case of a periodic function F with period λ, that is, F(x + λ − vt) = F(x − vt), the periodicity of F in space means that a snapshot of the wave at a given time t finds the wave varying periodically in space with period λ (sometimes called the wavelength of the wave). In a similar fashion, this periodicity of F implies a periodicity in time as well: F(x − v(t + T)) = F(x − vt) provided vT = λ, so an observation of the wave at a fixed location x finds the wave undulating periodically in time with period T = λ/v.^[6]

Phase velocity and group velocity

Frequency dispersion in groups of gravity waves on the surface of deep water. The red dot moves with the phase velocity, and the green dots propagate with the group velocity.

There are two velocities that are associated with waves, the phase velocity and the group velocity. To understand them, one must consider several types of waveform. For simplification, examination is restricted to one dimension.

The most basic wave (a form of plane wave) may be expressed in the form:

$\psi (x, \ t) = A e^{i \left( kx - \omega t \right)} \ ,$

which can be related to the usual sine and cosine forms using Euler's formula. Rewriting the argument, 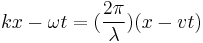$kx-\omega t = (\frac{2\pi}{\lambda})(x - vt)$ , makes clear that this expression describes a vibration of wavelength 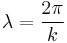$\lambda = \frac{2\pi}{k}$ traveling in the x-direction with a constant phase velocity 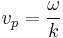$v_p = \frac{\omega}{k}\,$ ^[7].

The other type of wave to be considered is one with localized structure described by an envelope, which may be expressed mathematically as, for example:

$\psi (x, \ t) = \int_{-\infty} ^{\infty}\ dk_1 \ A(k_1)\ e^{i\left(k_1x - \omega t \right)} \ ,$

where now A(k₁) (the integral is the inverse fourier transform of A(k1)) is a function exhibiting a sharp peak in a region of wave vectors Δk surrounding the point k₁ = k. In exponential form:

$A = A_o (k_1) e^ {i \alpha (k_1)} \ ,$

with A_o the magnitude of A. For example, a common choice for A_o is a Gaussian wave packet:^[8]

$A_o (k_1) = N\ e^{-\sigma^2 (k_1-k)^2 / 2} \ ,$

where σ determines the spread of k₁-values about k, and N is the amplitude of the wave.

The exponential function inside the integral for ψ oscillates rapidly with its argument, say φ(k₁), and where it varies rapidly, the exponentials cancel each other out, interfere destructively, contributing little to ψ.^[7] However, an exception occurs at the location where the argument φ of the exponential varies slowly. (This observation is the basis for the method of stationary phase for evaluation of such integrals.^[9]) The condition for φ to vary slowly is that its rate of change with k₁ be small; this rate of variation is:^[7]

$\left . \frac{d \varphi }{d k_1} \right | _{k_1 = k } = x - t \left . \frac{d \omega}{dk_1}\right | _{k_1 = k } +\left . \frac{d \alpha}{d k_1}\right | _{k_1 = k } \ ,$

where the evaluation is made at k₁ = k because A(k₁) is centered there. This result shows that the position x where the phase changes slowly, the position where ψ is appreciable, moves with time at a speed called the group velocity:

$v_g = \frac{d \omega}{dk} \ .$

The group velocity therefore depends upon the dispersion relation connecting ω and k. For example, in quantum mechanics the energy of a particle represented as a wave packet is E = ħω = (ħk)²/(2m). Consequently, for that wave situation, the group velocity is

$v_g = \frac {\hbar k}{m} \ ,$

showing that the velocity of a localized particle in quantum mechanics is its group velocity.^[7] Because the group velocity varies with k, the shape of the wave packet broadens with time, and the particle becomes less localized.^[10] In other words, the velocity of the constituent waves of the wave packet travel at a rate that varies with their wavelength, so some move faster than others, and they cannot maintain the same interference pattern as the wave propagates.

Modulated waves

Illustration of the envelope (the slowly varying red curve) of an amplitude modulated wave. The fast varying blue curve is the carrier wave, which is being modulated.

Main article: Amplitude modulation

See also: Frequency modulation and Phase modulation

The amplitude of a wave may be constant (in which case the wave is a c.w. or continuous wave), or may be modulated so as to vary with time and/or position. The outline of the variation in amplitude is called the envelope of the wave. Mathematically, the modulated wave can be written in the form:^[11]^[12]^[13]

$u(x, \ t) = A(x, \ t)\sin (kx - \omega t + \phi) \ ,$

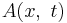where $A(x,\ t)$ is the amplitude envelope of the wave, 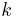$k$ is the wave number and $\phi$ is the phase. If the group velocity (see below) is wavelength independent, this equation can be simplified as:^[14]

$u(x, \ t) = A(x - v_g \ t)\sin (kx - \omega t + \phi) \ ,$

where v_g is the group velocity, showing that the envelope moves with velocity v_g and retains its shape. Otherwise, in cases where the group velocity varies with wavelength, the pulse shape changes in a manner often described using an envelope equation.^[14]^[15]

Sinusoidal waves

Mathematically, the most basic wave is the sine wave (or harmonic wave or sinusoid), with an amplitude u described by the equation:

$u(x, \ t)= A \sin (kx - \omega t + \phi) \ ,$

Graphic of the $y=\sin[2\pi(\frac{x}{2\pi}-\frac{t}{2\pi})]$ progressive sinusoidal wave.

where A is the amplitude of the wave – the maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave; x is the space coordinate, t is the time coordinate, k is the wavenumber (spatial frequency), ω is the temporal frequency, and φ is a phase offset.

The units of the amplitude depend on the type of wave — waves on a string have an amplitude expressed as a distance (meters), sound waves as pressure (pascals) and electromagnetic waves as the amplitude of the electric field (volts/meter).

The wavelength (denoted as λ) is the distance between two sequential crests (or troughs), and generally is measured in meters.

A wavenumber k, the spatial frequency of the wave in radians per unit distance (typically per meter), can be associated with the wavelength by the relation

$k = \frac{2 \pi}{\lambda}. \,$

Sine waves correspond to simple harmonic motion.

The period T is the time for one complete cycle of an oscillation of a wave. The frequency f (also frequently denoted as ν ) is the number of periods per unit time (per second) and is measured in hertz. These are related by:

$f=\frac{1}{T}. \,$

In other words, the frequency and period of a wave are reciprocals.

The angular frequency ω represents the frequency in radians per second. It is related to the frequency by

$\omega = 2 \pi f = \frac{2 \pi}{T}. \,$

The wavelength λ of a sinusoidal waveform traveling at constant speed v is given by:^[16]

$\lambda = \frac{v}{f},$

where v is called the phase speed (magnitude of the phase velocity) of the wave and f is the wave's frequency.

Wavelength can be a useful concept even if the wave is not periodic in space. For example, in an ocean wave approaching shore, shown in the figure, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The analysis of the wave can be based upon comparison of the local wavelength with the local water depth.^[17]

Although arbitrary wave shapes will propagate unchanged in lossless linear time-invariant systems, in the presence of dispersion the sine wave is the unique shape that will propagate unchanged but for phase and amplitude, making it easy to analyze.^[18] Due to the Kramers–Kronig relations, a linear medium with dispersion also exhibits loss, so the sine wave propagating in a dispersive medium is attenuated in certain frequency ranges that depend upon the medium.^[19] The sine function is periodic, so the sine wave or sinusoid has a wavelength in space and a period in time.^[20]^[21]

The sinusoid is defined for all times and distances, whereas in physical situations we usually deal with waves that exist for a limited span in space and duration in time. Fortunately, an arbitrary wave shape can be decomposed into an infinite set of sinusoidal waves by the use of Fourier analysis. As a result, the simple case of a single sinusoidal wave can be applied to more general cases.^[22]^[23] In particular, many media are linear, or nearly so, so the calculation of arbitrary wave behavior can be found by adding up responses to individual sinusoidal waves using the superposition principle to find the solution for a general waveform.^[24] When a medium is nonlinear, the response to complex waves cannot be determined from a sine-wave decomposition.

Plane waves

Standing waves

Main article: Standing wave

Standing wave in stationary medium. The red dots represent the wave nodes

A standing wave, also known as a stationary wave, is a wave that remains in a constant position. This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling in opposite directions.

The sum of two counter-propagating waves (of equal amplitude and frequency) creates a standing wave. Standing waves commonly arise when a boundary blocks further propagation of the wave, thus causing wave reflection, and therefore introducing a counter-propagating wave. For example when a violin string is displaced, longitudinal waves propagate out to where the string is held in place at the bridge and the "nut", whereupon the waves are reflected back. At the bridge and nut, the two opposed waves are in antiphase and cancel each other, producing a node. Halfway between two nodes there is an antinode, where the two counter-propagating waves enhance each other maximally. There is on average no net propagation of energy.

Also see: Acoustic resonance, Helmholtz resonator, and organ pipe

Physical properties

Light beam exhibiting reflection, refraction, transmission and dispersion when encountering a prism

Periodic waves are characterized by crests (highs) and troughs (lows), and may usually be categorized as either longitudinal or transverse. Transverse waves are those with vibrations perpendicular to the direction of the propagation of the wave; examples include waves on a string, and electromagnetic waves. Longitudinal waves are those with vibrations parallel to the direction of the propagation of the wave; examples include most sound waves.

When an object bobs up and down on a ripple in a pond, it experiences an orbital trajectory because ripples are not simple transverse sinusoidal waves.

All waves have common behavior under a number of standard situations. All waves can undergo the following:

Reflection — change in wave direction after it strikes a reflective surface, causing the angle the wave makes with the reflective surface in relation to a normal line to the surface to equal the angle the reflected wave makes with the same normal line

Rectilinear propagation — the movement of waves in a straight line, in the absence of any obstacles or change in media

Interference

Main article: Interference (wave propagation)

Waves that encounter each other combine through superposition to create a new wave called an interference pattern. Important interference patterns occur for waves that are in phase

Reflection, absorption and transmission

Main articles: Reflection, Absorption (acoustics), Absorption (electromagnetic radiation), Transmission, and Transmission medium

The medium that carries a wave is called a transmission medium. It can be classified into one or more of the following categories:

A bounded medium if it is finite in extent, otherwise an unbounded medium
A linear medium if the amplitudes of different waves at any particular point in the medium can be added
A uniform medium or homogeneous medium if its physical properties are unchanged at different locations in space
An isotropic medium if its physical properties are the same in different directions

Refraction

Main article: Refraction

Sinusoidal traveling plane wave entering a region of lower wave velocity at an angle, illustrating the decrease in wavelength and change of direction (refraction) that results.

Refraction is the phenomenon of a wave changing it's speed. Mathematically, this means that the size of the phase velocity changes. Typically, refraction occurs when a wave passes from one medium into another. The amount by which a wave is refracted by a material is given by the refractive index of the material. The directions of incidence and refraction are related to the refractive indices of the two materials by Snell's law.

Diffraction

Main article: Diffraction

A wave exhibits diffraction when it encounters an obstacle that bends the wave or when it spreads after emerging from an opening. Diffraction effects are more pronounced when the size of the obstacle or opening is comparable to the wavelength of the wave.

Polarization

Main article: Polarization (waves)

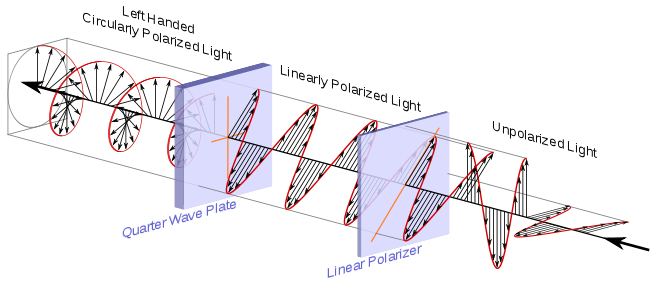
A wave is polarized if it oscillates in one direction or plane. A wave can be polarized by the use of a polarizing filter. The polarization of a transverse wave describes the direction of oscillation in the plane perpendicular to the direction of travel.

Longitudinal waves such as sound waves do not exhibit polarization. For these waves the direction of oscillation is along the direction of travel.

Dispersion

Main articles: Dispersion (optics) and Dispersion (water waves)

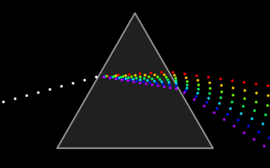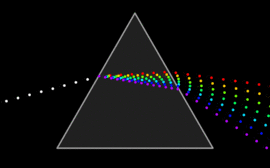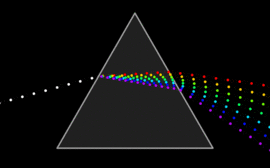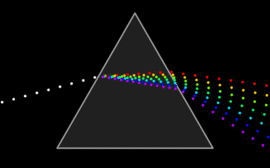
A wave undergoes dispersion when either the phase velocity or the group velocity depends on the wave frequency. Dispersion is most easily seen by letting white light pass through a prism, the result of which is to produce the spectrum of colours of the rainbow. Isaac Newton performed experiments with light and prisms, presenting his findings in the Opticks (1704) that white light consists of several colours and that these colours cannot be decomposed any further. ^[25]

Mechanical waves

Waves on strings

The speed of a wave traveling along a vibrating string ( v ) is directly proportional to the square root of the tension of the string ( T ) over the linear mass density ( μ ):

$v=\sqrt{\frac{T}{\mu}}, \,$

where the linear density μ is the mass per unit length of the string.

Acoustic waves

Acoustic or sound waves travel at speed given by

$v=\sqrt{\frac{B}{\rho_0}}, \,$

or the square root of the adiabatic bulk modulus divided by the ambient fluid density (see speed of sound).

Water waves

Main article: Water waves

Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
Sound — a mechanical wave that propagates through gases, liquids, solids and plasmas
Inertial waves, which occur in rotating fluids and are restored by the Coriolis effect
Ocean surface waves, which are perturbations that propagate through water

Seismic waves

Main article: Seismic waves

Seismic waves in earthquakes, of which there are three types, called S, P, and L

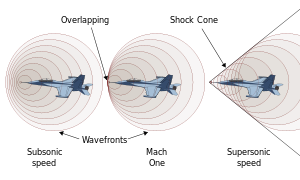
Shock waves

Main article: Shock wave

See also: Sonic boom and Cerenkov radiation

Other

Waves of traffic, that is, propagation of different densities of motor vehicles, and so forth, which can be modeled as kinematic waves^[26]

Electromagnetic waves

Main articles: Electromagnetic radiation and Electromagnetic spectrum

(infrared, micro, radio, visible, uv)

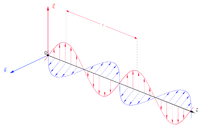
An electromagnetic wave consists of two waves that are oscillations of the electric and magnetic fields. An electromagnetic wave travels in a direction that is at right angles to the oscillation direction of both fields. In the 19th century, James Clerk Maxwell showed that, in vacuum, the electric and magnetic fields satisfy the wave equation both with speed equal to that of the speed of light. From this emerged the idea that light is an electromagnetic wave. Electromagnetic waves can have different frequencies (and thus wavelengths), giving rise to various types of radiation such as, infrared, radio waves, visible light, ultraviolet, microwaves and X-rays.

Quantum mechanical waves

Main article: Schrödinger equation

de Broglie waves

Main articles: Wave packet and Matter wave

Louis de Broglie postulated that all particles with momentum have a wavelength

$\lambda = \frac{h}{p},$

where h is Planck's constant, and p is the magnitude of the momentum of the particle. This hypothesis was at the basis of quantum mechanics. Nowadays, this wavelength is called the de Broglie wavelength. For example, the electrons in a CRT display have a de Broglie wavelength of about 10⁻¹³ m.

A wave representing such a particle traveling in the k-direction is expressed by the wave function:

$\psi (\mathbf{r}, \ t=0) =A\ e^{i\mathbf{k \cdot r}} \ ,$

where the wavelength is determined by the wave vector k as:

$\lambda = \frac {2 \pi}{k} \ ,$

and the momentum by:

$\mathbf p = \hbar \mathbf{k} \ .$

However, a wave like this with definite wavelength is not localized in space, and so cannot represent a particle localized in space. To localize a particle, de Broglie proposed a superposition of different wavelengths ranging around a central value in a wave packet,^[28] a waveform often used in quantum mechanics to describe the wave function of a particle. In a wave packet, the wavelength of the particle is not precise, and the local wavelength deviates on either side of the main wavelength value.

In representing the wave function of a localized particle, the wave packet is often taken to have a Gaussian shape and is called a Gaussian wave packet.^[29] Gaussian wave packets also are used to analyze water waves.^[30]

For example, a Gaussian wavefunction ψ might take the form:^[31]

$\psi(x,\ t=0) = A\ \exp \left( -\frac{x^2}{2\sigma^2} + i k_0 x \right) \ ,$

at some initial time t = 0, where the central wavelength is related to the central wave vector k₀ as λ₀ = 2π / k₀. It is well known from the theory of Fourier analysis,^[32] or from the Heisenberg uncertainty principle (in the case of quantum mechanics) that a narrow range of wavelengths is necessary to produce a localized wave packet, and the more localized the envelope, the larger the spread in required wavelengths. The Fourier transform of a Gaussian is itself a Gaussian.^[33] Given the Gaussian:

$f(x) = e^{-x^2 / (2\sigma^2)} \ ,$

the Fourier transform is:

$\tilde{ f} (k) = \sigma e^{-\sigma^2 k^2 / 2} \ .$

The Gaussian in space therefore is made up of waves:

$f(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \ \tilde{f} (k) e^{ikx} \ dk \�;$

that is, a number of waves of wavelengths λ such that kλ = 2 π.

The parameter σ decides the spatial spread of the Gaussian along the x-axis, while the Fourier transform shows a spread in wave vector k determined by 1/σ. That is, the smaller the extent in space, the larger the extent in k, and hence in λ = 2π/k.

Gravitational waves

Main article: Gravitational wave

Animation showing the effect of a cross-polarized gravitational wave on a ring of test particles

Not to be confused with gravity waves, gravitational waves are disturbances in the curvature of spacetime, predicted by Einstein's theory of General Relativity.

WKB method

Main article: WKB method

In a nonuniform medium, in which the wavenumber k can depend on the location as well as the frequency, the phase term kx is typically replaced by the integral of k(x)dx, according to the WKB method. Such nonuniform traveling waves are common in many physical problems, including the mechanics of the cochlea and waves on hanging ropes.

Notes

↑ Lev A. Ostrovsky & Alexander I. Potapov (2002). Modulated waves: theory and application. John Hopkins University Press. ISBN 0801873258. http://www.amazon.com/gp/product/0801873258.
↑ Michael A. Slawinski, Klause Helbig (2003). "Wave equations". Seismic waves and rays in elastic media. Elsevier. pp. 131 ff. ISBN 0080439306. http://books.google.com/?id=s7bp6ezoRhcC&pg=PA134.
↑ Jalal M. Ihsan Shatah, Michael Struwe (2000). "The linear wave equation". Geometric wave equations. American Mathematical Society Bookstore. pp. 37 ff. ISBN 0821827499. http://books.google.com/?id=zsasG2axbSoC&pg=PA37.
↑ Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13–14. http://books.google.com/?id=5cZFRwLuhdQC&printsec=frontcover.
↑ Louis Lyons (1998). All you wanted to know about mathematics but were afraid to ask. Cambridge University Press. pp. 128 ff. ISBN 052143601X. http://books.google.com/?id=WdPGzHG3DN0C&pg=PA128.
↑ Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 ed.). Wiley. p. 77. ISBN 0470185902. http://books.google.com/?id=o7sXm2GSr9IC&pg=PA77.
↑ ^7.0 ^7.1 ^7.2 ^7.3 Albert Messiah (1999). Quantum Mechanics (Reprint of two-volume Wiley 1958 ed.). Courier Dover. pp. 50–52. ISBN 9780486409245. http://books.google.com/?id=mwssSDXzkNcC&pg=PA52&dq=intitle:quantum+inauthor:messiah+%22group+velocity%22+%22center+of+the+wave+packet%22.
↑ See, for example, Eq. 2(a) in Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics: An introduction (2nd ed.). Springer. pp. 60–61. ISBN 3540674586. http://books.google.com/?id=7qCMUfwoQcAC&pg=PA61.
↑ John W. Negele, Henri Orland (1998). Quantum many-particle systems (Reprint in Advanced Book Classics ed.). Westview Press. p. 121. ISBN 0738200522. http://books.google.com/?id=mx5CfeeEkm0C&pg=PA121.
↑ Donald D. Fitts (1999). Principles of quantum mechanics: as applied to chemistry and chemical physics. Cambridge University Press. pp. 15 ff. ISBN 0521658411. http://books.google.com/?id=8t4DiXKIvRgC&pg=PA15.
↑ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. p. 9. ISBN 3865374190. http://books.google.com/?id=6kOoT_AX2CwC&pg=PA9.
↑ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. p. 365. ISBN 354062001X. http://books.google.com/?id=geYKPFoLgoMC&pg=PA365.
↑ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. p. 33. ISBN 0521631343. http://books.google.com/?id=FTdDMtpkSkIC&pg=PA33.
↑ ^14.0 ^14.1 Chin-Lin Chen (2006). "§13.7.3 Pulse envelope in nondispersive media". Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/?id=LxzWPskhns0C&pg=PA363.
↑ Stefano Longhi, Davide Janner (2008). "Localization and Wannier wave packets in photonic crystals". In Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami. Localized Waves. Wiley-Interscience. p. 329. ISBN 0470108851. http://books.google.com/?id=xxbXgL967PwC&pg=PA329.
↑ David C. Cassidy, Gerald James Holton, Floyd James Rutherford (2002). Understanding physics. Birkhäuser. pp. 339 ff. ISBN 0387987568. http://books.google.com/?id=rpQo7f9F1xUC&pg=PA340.
↑ Paul R Pinet. op. cit.. p. 242. ISBN 0763759937. http://books.google.com/?id=6TCm8Xy-sLUC&pg=PA242.
↑ Mischa Schwartz, William R. Bennett, and Seymour Stein (1995). Communication Systems and Techniques. John Wiley and Sons. p. 208. ISBN 9780780347151. http://books.google.com/?id=oRSHWmaiZwUC&pg=PA208&dq=sine+wave+medium++linear+time-invariant.
↑ See Eq. 5.10 and discussion in A. G. G. M. Tielens (2005). The physics and chemistry of the interstellar medium. Cambridge University Press. pp. 119 ff. ISBN 0521826349. http://books.google.com/?id=wMnvg681JXMC&pg=PA119. ; Eq. 6.36 and associated discussion in Otfried Madelung (1996). Introduction to solid-state theory (3rd ed.). Springer. pp. 261 ff. ISBN 354060443X. http://books.google.com/?id=yK_J-3_p8_oC&pg=PA261. ; and Eq. 3.5 in F Mainardi (1996). "Transient waves in linear viscoelastic media". In Ardéshir Guran, A. Bostrom, Herbert Überall, O. Leroy. Acoustic Interactions with Submerged Elastic Structures: Nondestructive testing, acoustic wave propagation and scattering. World Scientific. p. 134. ISBN 9810242719. http://books.google.com/?id=UfSk45nCVKMC&pg=PA134.
↑ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. p. 106. ISBN 0817636358. http://books.google.com/?id=TC4MCYBSJJcC&pg=PA106.
↑ Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. p. 31. ISBN 0865420785. http://books.google.com/?id=Kf8fyvRd280C&pg=PA31.
↑ Seth Stein, Michael E. Wysession. op. cit.. p. 32. ISBN 0865420785. http://books.google.com/?id=Kf8fyvRd280C&pg=PA32.
↑ Kimball A. Milton, Julian Seymour Schwinger (2006). Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer. p. 16. ISBN 3540293043. http://books.google.com/?id=x_h2rai2pYwC&pg=PA16. "Thus, an arbitrary function f(r, t) can be synthesized by a proper superposition of the functions exp[i (k·r−ωt)]…"
↑ Raymond A. Serway and John W. Jewett (2005). "§14.1 The Principle of Superposition". Principles of physics (4th ed.). Cengage Learning. p. 433. ISBN 053449143X. http://books.google.com/?id=1DZz341Pp50C&pg=PA433.
↑ Newton, Isaac (1704). "Prop VII Theor V". Opticks: Or, A treatise of the Reflections, Refractions, Inflexions and Colours of Light. Also Two treatises of the Species and Magnitude of Curvilinear Figures. 1. London. p. 118. http://gallica.bnf.fr/ark:/12148/bpt6k3362k.image.f128.pagination. "All the Colours in the Universe which are made by Light... are either the Colours of homogeneal Lights, or compounded of these..."
↑ M. J. Lighthill; G. B. Whitham (1955). "On kinematic waves. II. A theory of traffic flow on long crowded roads". Proceedings of the Royal Society of London. Series A 229: 281–345. And: P. I. Richards (1956). "Shockwaves on the highway". Operations Research 4: 42–51. doi:10.1287/opre.4.1.42.
↑ A. T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN 0486667413. http://books.google.com/?id=3SOwc6npkIwC&pg=PA59. "(p. 61) …the individual waves move more slowly than the packet and therefore pass back through the packet as it advances"
↑ Ming Chiang Li (1980). "Electron Interference". In L. Marton & Claire Marton. Advances in Electronics and Electron Physics. 53. Academic Press. p. 271. ISBN 0120146533. http://books.google.com/?id=g5q6tZRwUu4C&pg=PA271.
↑ See for example Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2 ed.). Springer. p. 60. ISBN 3540674586. http://books.google.com/?id=7qCMUfwoQcAC&pg=PA60. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. p. 57. ISBN 0521620058. http://books.google.com/?id=YWd7zHU0U7UC&pg=PA57. ,Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Press. p. 17. ISBN 0521658411. http://books.google.com/?id=8t4DiXKIvRgC&pg=PA17. .
↑ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2nd ed.). World Scientific. p. 47. ISBN 9971507897. http://books.google.com/?id=WHMNEL-9lqkC&pg=PA47.
↑ Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2nd ed.). Springer. p. 60. ISBN 3540674586. http://books.google.com/?id=7qCMUfwoQcAC&pg=PA60.
↑ Siegmund Brandt, Hans Dieter Dahmen (2001). The picture book of quantum mechanics (3rd ed.). Springer. p. 23. ISBN 0387951415. http://books.google.com/?id=VM4GFlzHg34C&pg=PA23.
↑ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. p. 677. ISBN 0521598273. http://books.google.com/?id=QKsiFdOvcwsC&pg=PA677.

Bibliography

Sources

Campbell, M. and Greated, C. (1987). The Musician’s Guide to Acoustics. New York: Schirmer Books.
French, A.P. (1971). Vibrations and Waves (M.I.T. Introductory physics series). Nelson Thornes. ISBN 0-393-09936-9. OCLC 163810889.
Hall, D. E. (1980). Musical Acoustics: An Introduction. Belmont, California: Wadsworth Publishing Company. ISBN 0534007589. .
Hunt, F. V. (1992). Origins in Acoustics. New York: Acoustical Society of America Press. http://asa.aip.org/publications.html#pub17. .
Ostrovsky, L. A.; Potapov, A. S. (1999). Modulated Waves, Theory and Applications. Baltimore: The Johns Hopkins University Press. ISBN 0801858704. .
Vassilakis, P.N. (2001). Perceptual and Physical Properties of Amplitude Fluctuation and their Musical Significance. Doctoral Dissertation. University of California, Los Angeles.

External links

Velocities of waves
Phase velocity • Group velocity • Front velocity • Signal velocity