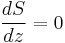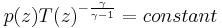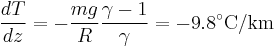Troposphere

Earth atmosphere diagram showing the exosphere and other layers. The layers are to scale. From Earth's surface to the top of the stratosphere (50km) is just under 1% of Earth's radius.

A view of Earth's troposphere from an airplane.

Atmospheric circulation shown with three large cells.

The troposphere is the lowest portion of Earth's atmosphere. It contains approximately 75% of the atmosphere's mass and 99% of its water vapor and aerosols.

The average depth of the troposphere is approximately 17 km (11 mi) in the middle latitudes. It is deeper in the tropical regions, up to 20 km (12 mi), and shallower near the poles, at 7 km (4.3 mi) in summer, and indistinct in winter. The lowest part of the troposphere, where friction with the Earth's surface influences air flow, is the planetary boundary layer. This layer is typically a few hundred meters to 2 km (1.2 mi) deep depending on the landform and time of day. The border between the troposphere and stratosphere, called the tropopause, is a temperature inversion.^[1]

The word troposphere derives from the Greek: tropos for "turning" or "mixing," reflecting the fact that turbulent mixing plays an important role in the troposphere's structure and behavior. Most of the phenomena we associate with day-to-day weather occur in the troposphere.^[1]

1 Pressure and temperature structure
2 References
3 External links

Pressure and temperature structure

Composition

The chemical composition of the troposphere is essentially uniform, with the notable exception of water vapor. The source of water vapor is at the surface through the processes of evaporation and transpiration. Furthermore the temperature of the troposphere decreases with height, and saturation vapor pressure decreases strongly as temperature drops, so the amount of water vapor that can exist in the atmosphere decreases strongly with height. Thus the proportion of water vapor is normally greatest near the surface and decreases with height.

Pressure

The pressure of the atmosphere is maximum at sea level and decreases with higher altitude. This is because the atmosphere is very nearly in hydrostatic equilibrium, so that the pressure is equal to the weight of air above a given point. The change in pressure with height therefore can be equated to the density with this hydrostatic equation:^[2]

$\frac{dp}{dz} = -\rho g_n = - \frac {mpg}{RT}$

where:

g_n stands for the standard gravity
ρ stands for density
z stands for height
p stands for pressure
R stands for the gas constant
T stands for temperature in kelvins
m stands for the molar mass

Since temperature in principle also depends on altitude, one needs a second equation to determine the pressure as a function of height, as discussed in the next section.*

Temperature

The temperature of the troposphere generally decreases as altitude increases. The rate at which the temperature decreases, $-dT/dz$ , is called the environmental lapse rate (ELR). The ELR is nothing more the difference in temperature between the surface and the tropopause divided by the height. The reason for this temperature difference is the absorption of the suns energy occurs at the ground which heats the lower levels of the atmosphere, and the radiation of heat occurs at the top of the atmosphere cooling the earth, this process maintaining the overall heat balance of the earth.

As parcels of air in the atmosphere rise and fall, they also undergo changes in temperature for reasons described below. The rate of change of the temperature in the parcel may be less than or more than the ELR. When a parcel of air rises, it expands, because the pressure is lower at higher altitudes. As the air parcel expands, it pushes on the air around it, doing work; but generally it does not gain heat in exchange from its environment, because its thermal conductivity is low (such a process is called adiabatic). Since the parcel does work and gains no heat, it loses energy, and so its temperature decreases. (The reverse, of course, will be true for a sinking parcel of air.) ^[1]

Since the heat exchanged dQ is related to the entropy change dS by dQ=T dS, the equation governing the temperature as a function of height for a thoroughly mixed atmosphere is

$\frac{dS}{dz} = 0$

where S is the entropy. The rate at which temperature decreases with height under such conditions is called the adiabatic lapse rate.

For dry air, which is approximately an ideal gas, we can proceed further. The adiabatic equation for an ideal gas is ^[3]

$p(z)T(z)^{-\frac{\gamma}{\gamma-1}}=constant$

where $\gamma$ is the heat capacity ratio ( $\gamma$ =7/5, for air). Combining with the equation for the pressure, one arrives at the dry adiabatic lapse rate,^[4]

$\frac{dT}{dz}=- \frac{mg}{R} \frac{\gamma-1}{\gamma}=-9.8^{\circ}\mathrm{C}/\mathrm{km}$

If the air contains water vapor, then cooling of the air can cause the water to condense, and the behavior is no longer that of an ideal gas. If the air is at the saturated vapor pressure, then the rate at which temperature drops with height is called the saturated adiabatic lapse rate. More generally, the actual rate at which the temperature drops with altitude is called the environmental lapse rate. In the troposphere, the average environmental lapse rate is a drop of about 6.5 °C for every 1 km (1000 meters) increase in height. ^[1]

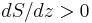The environmental lapse rate (the actual rate at which temperature drops with height, $dT/dz$ ) is not usually equal to the adiabatic lapse rate (or correspondingly, $dS/dz \ne 0$ ). If the upper air is warmer than predicted by the adiabatic lapse rate ( $dS/dz > 0$ ), then when a parcel of air rises and expands, it will arrive at the new height at a lower temperature than its surroundings. In this case, the air parcel is denser than its surroundings, so it sinks back to its original height, and the air is stable against being lifted. If, on the contrary, the upper air is cooler than predicted by the adiabatic lapse rate, then when the air parcel rises to its new height it will have a higher temperature and a lower density than its surroundings, and will continue to accelerate upward.^[1]^[2]

Temperatures decrease at middle latitudes from an average of 15°C at sea level to about -55°C at the top of the tropopause. At the poles, the troposphere is thinner and the temperature only decreases to -45°C, while at the equator the temperature at the top of the troposphere can reach -75°C.

Tropopause

The tropopause is the boundary region between the troposphere and the stratosphere.

Measuring the temperature change with height through the troposphere and the stratosphere identifies the location of the tropopause. In the troposphere, temperature decreases with altitude. In the stratosphere, however, the temperature remains constant for a while and then increases with altitude. The region of the atmosphere where the lapse rate changes from positive (in the troposphere) to negative (in the stratosphere), is defined as the tropopause.^[1] Thus, the tropopause is an inversion layer, and there is little mixing between the two layers of the atmosphere.

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 Danielson, Levin, and Abrams, Meteorology, McGraw Hill, 2003
↑ ^2.0 ^2.1 Landau and Lifshitz, Fluid Mechanics, Pergamon, 1979
↑ Landau and Lifshitz, Statistical Physics Part 1, Pergamon, 1980
↑ Kittel and Kroemer, Thermal Physics, Freeman, 1980; chapter 6, problem 11

External links

Composition of the Atmosphere, from the University of Tennessee Physics dept.
Chemical Reactions in the Atmosphere

Earth's atmosphere

Troposphere • Stratosphere • Mesosphere • Thermosphere • Exosphere

Tropopause • Stratopause • Mesopause • Thermopause / Exobase

Ozone layer • Turbopause • Ionosphere