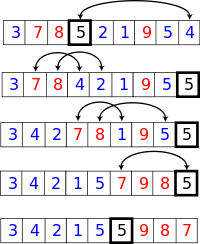
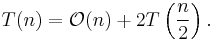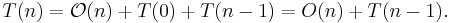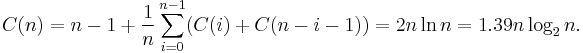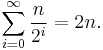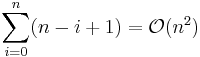Quicksort

Quicksort
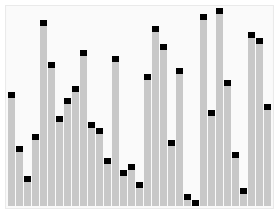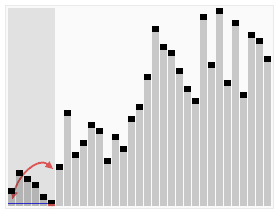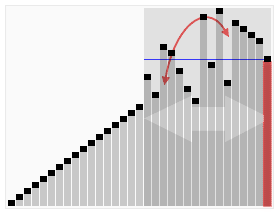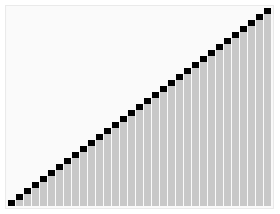Visualization of the quicksort algorithm. The horizontal lines are pivot values.
Class	Sorting algorithm
Worst case performance	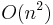${O}(n^2)$
Best case performance	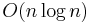${O}(n\log n)$
Average case performance	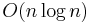${O}(n\log n)$
Worst case space complexity	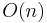${O}(n)$

Quicksort is a sorting algorithm developed by C. A. R. Hoare that, on average, makes 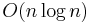${O}(n\log n)$ (big O notation) comparisons to sort n items. In the worst case, it makes 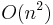${O}(n^2)$ comparisons, though if implemented correctly this behavior is rare. Typically, quicksort is significantly faster in practice than other 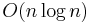${O}(n\log n)$ algorithms, because its inner loop can be efficiently implemented on most architectures, and in most real-world data, it is possible to make design choices that minimize the probability of requiring quadratic time. Additionally, quicksort tends to make excellent usage of the memory hierarchy, taking perfect advantage of virtual memory and available caches. Coupled with the fact that quicksort is an in-place sort and uses no temporary memory, it is very well suited to modern computer architectures.

Quicksort (also known as "partition-exchange sort") is a comparison sort and, in efficient implementations, is not a stable sort.

1 History
2 Algorithm
- 2.1 Parallelizations
3 Formal analysis
4 Selection-based pivoting
5 Variants
6 Comparison with other sorting algorithms
7 See also
8 Notes
9 References
10 External links

History

The quicksort algorithm was developed in 1960 by C. A. R. Hoare while in the Soviet Union, as a visiting student at Moscow State University. At that time, Hoare worked in a project on machine translation for the National Physical Laboratory. He developed the algorithm in order to sort the words to be translated, to make them more easily matched to an already-sorted Russian-to-English dictionary that was stored on magnetic tape.^[1]

Algorithm

Full example of quicksort on a random set of numbers. The boxed element is the pivot. It is always chosen as the last element of the partition. However, always choosing the last element in the partition as the pivot in this way results in poor performance ( $O(n^2)$ ) on already sorted lists, or lists of identical elements. Since sub-lists of sorted / identical elements crop up a lot towards the end of a sorting procedure on a large set, versions of the quicksort algorithm which choose the pivot as the middle element run much more quickly than the algorithm described in this diagram on large sets of numbers.

Quicksort sorts by employing a divide and conquer strategy to divide a list into two sub-lists.

The steps are:

Pick an element, called a pivot, from the list.
Reorder the list so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
Recursively sort the sub-list of lesser elements and the sub-list of greater elements.

The base case of the recursion are lists of size zero or one, which never need to be sorted.

In simple pseudocode, the algorithm might be expressed as this:

 function quicksort(array)
     var list less, greater
     if length(array) ≤ 1  
         return array  
     select and remove a pivot value pivot from array
     for each x in array
         if x < pivot then append x to less
         else if x > pivot then append x to greater
     return concatenate(quicksort(less), pivot, quicksort(greater))

Notice that we only examine elements by comparing them to other elements. This makes quicksort a comparison sort. This version is also a stable sort (assuming that the "for each" method retrieves elements in original order, and the pivot selected is the last among those of equal value).

The correctness of the partition algorithm is based on the following two arguments:

At each iteration, all the elements processed so far are in the desired position: before the pivot if less than the pivot's value, after the pivot if greater than the pivot's value (loop invariant).
Each iteration leaves one fewer element to be processed (loop variant).

The correctness of the overall algorithm follows from inductive reasoning: for zero or one element, the algorithm leaves the data unchanged; for a larger data set it produces the concatenation of two parts, elements less than the pivot and elements greater than it, themselves sorted by the recursive hypothesis.

The disadvantage of the simple version above is that it requires 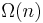$\Omega(n)$ extra storage space, which is as bad as merge sort. The additional memory allocations required can also drastically impact speed and cache performance in practical implementations. There is a more complex version which uses an in-place partition algorithm and can achieve the complete sort using 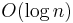$O(\log n)$ space (not counting the input) use on average (for the call stack):

  function partition(array, left, right, pivotIndex)
     pivotValue := array[pivotIndex]
     swap array[pivotIndex] and array[right] // Move pivot to end
     storeIndex := left
     for i  from  left to right - 1 // left ≤ i < right  
         if array[i] ≤ pivotValue 
             swap array[i] and array[storeIndex]
             storeIndex := storeIndex + 1
     swap array[storeIndex] and array[right] // Move pivot to its final place
     return storeIndex

In-place partition in action on a small list. The boxed element is the pivot element, blue elements are less or equal, and red elements are larger.

This is the in-place partition algorithm. It partitions the portion of the array between indexes left and right, inclusively, by moving all elements less than or equal to array[pivotIndex] to the beginning of the subarray, leaving all the greater elements following them. In the process it also finds the final position for the pivot element, which it returns. It temporarily moves the pivot element to the end of the subarray, so that it doesn't get in the way. Because it only uses exchanges, the final list has the same elements as the original list. Notice that an element may be exchanged multiple times before reaching its final place. Also, in case of pivot duplicates in the input array, they can be spread across left subarray, possibly in random order. This doesn't represent a partitioning failure, as further sorting will reposition and finally "glue" them together.

This form of the partition algorithm is not the original form; multiple variations can be found in various textbooks, such as versions not having the storeIndex. However, this form is probably the easiest to understand.

Once we have this, writing quicksort itself is easy:

 procedure quicksort(array, left, right)
     if right > left
         select a pivot index //(e.g. pivotIndex := left+(right-left)/2)
         pivotNewIndex := partition(array, left, right, pivotIndex)
         quicksort(array, left, pivotNewIndex - 1)
         quicksort(array, pivotNewIndex + 1, right)

However, since partition reorders elements within a partition, this version of quicksort is not a stable sort.

In very early versions of quicksort, the leftmost element of the partition would often be chosen as the pivot element. Unfortunately, this causes worst-case behavior on already sorted arrays, which is a rather common use-case. The problem was easily solved by choosing either a random index for the pivot, choosing the middle index of the partition or (especially for longer partitions) choosing the median of the first, middle and last element of the partition for the pivot (as recommended by R. Sedgewick).^[2]^[3]

Two other important optimizations, also suggested by R. Sedgewick, as commonly acknowledged, and widely used in practice^[4]^[5]^[6] are:

To make sure at most O(log N) space is used, recurse first into the smaller half of the array, and use a tail call to recurse into the other.
Use insertion sort, which has a smaller constant factor and is thus faster on small arrays, for invocations on such small arrays (i.e. where the length is less than a threshold t determined experimentally). This can be implemented by leaving such arrays unsorted and running a single insertion sort pass at the end, because insertion sort handles nearly sorted arrays efficiently. A separate insertion sort of each small segment as they are identified adds the overhead of starting and stopping many small sorts, but, avoids wasting effort comparing keys across the many segment boundaries, which keys will be in order due to the workings of the quicksort process.

Parallelizations

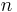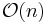Like merge sort, quicksort can also be easily parallelized due to its divide-and-conquer nature. Individual in-place partition operations are difficult to parallelize, but once divided, different sections of the list can be sorted in parallel. If we have $p$ processors, we can divide a list of $n$ elements into $p$ sublists in $\mathcal{O}(n)$ average time, then sort each of these in 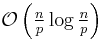$\textstyle\mathcal{O}\left(\frac{n}{p} \log\frac{n}{p}\right)$ average time. Ignoring the 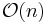$\mathcal{O}(n)$ preprocessing and the time required to merge the sorted sublists, this is linear speedup. Given 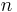$n$ processors, only 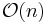$\mathcal{O}(n)$ time is required overall.

One advantage of parallel quicksort over other parallel sort algorithms is that no synchronization is required. A new thread is started as soon as a sublist is available for it to work on and it does not communicate with other threads. When all threads complete, the sort is done.

Other more sophisticated parallel sorting algorithms can achieve even better time bounds.^[7] For example, in 1991 David Powers described a parallelized quicksort that can operate in 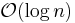$\mathcal{O}(\log n)$ time given enough processors by performing partitioning implicitly.^[8]

Formal analysis

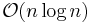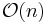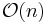From the initial description it's not obvious that quicksort takes $\mathcal{O}(n \log n)$ time on average. It's not hard to see that the partition operation, which simply loops over the elements of the array once, uses $\mathcal{O}(n)$ time. In versions that perform concatenation, this operation is also $\mathcal{O}(n)$ .

In the best case, each time we perform a partition we divide the list into two nearly equal pieces. This means each recursive call processes a list of half the size. Consequently, we can make only 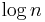$\log n$ nested calls before we reach a list of size 1. This means that the depth of the call tree is 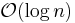$\mathcal{O}(\log n)$ . But no two calls at the same level of the call tree process the same part of the original list; thus, each level of calls needs only 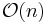$\mathcal{O}(n)$ time all together (each call has some constant overhead, but since there are only 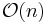$\mathcal{O}(n)$ calls at each level, this is subsumed in the 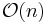$\mathcal{O}(n)$ factor). The result is that the algorithm uses only 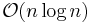$\mathcal{O}(n \log n)$ time.

An alternate approach is to set up a recurrence relation for the 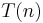$T(n)$ factor, the time needed to sort a list of size 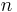$n$ . Because a single quicksort call involves 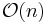$\mathcal{O}(n)$ factor work plus two recursive calls on lists of size 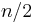$n/2$ in the best case, the relation would be:

$T(n) = \mathcal{O}(n) + 2T\left(\frac{n}{2}\right).$

The master theorem tells us that 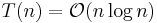$T(n) = \mathcal{O}(n \log n)$ .

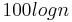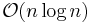In fact, it's not necessary to divide the list this precisely; even if each pivot splits the elements with 99% on one side and 1% on the other (or any other fixed fraction), the call depth is still limited to $100 log n$ , so the total running time is still $\mathcal{O}(n \log n)$ .

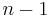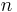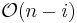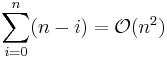In the worst case, however, the two sublists have size 1 and $n-1$ (for example, if the array consists of the same element by value), and the call tree becomes a linear chain of $n$ nested calls. The $i$ th call does $\mathcal{O}(n-i)$ work, and $\sum_{i=0}^n (n-i) = \mathcal{O}(n^2)$ . The recurrence relation is:

$T(n) = \mathcal{O}(n) + T(0) + T(n-1) = O(n) + T(n-1).$

This is the same relation as for insertion sort and selection sort, and it solves to 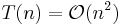$T(n) = \mathcal{O}(n^2)$ . Given knowledge of which comparisons are performed by the sort, there are adaptive algorithms that are effective at generating worst-case input for quicksort on-the-fly, regardless of the pivot selection strategy.^[9]

Randomized quicksort expected complexity

Randomized quicksort has the desirable property that, for any input, it requires only 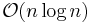$\mathcal{O}(n \log n)$ expected time (averaged over all choices of pivots). But what makes random pivots a good choice?

Suppose we sort the list and then divide it into four parts. The two parts in the middle will contain the best pivots; each of them is larger than at least 25% of the elements and smaller than at least 25% of the elements. If we could consistently choose an element from these two middle parts, we would only have to split the list at most 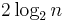$2 \log_2 n$ times before reaching lists of size 1, yielding an 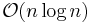$\mathcal{O}(n \log n)$ algorithm.

A random choice will only choose from these middle parts half the time. However, this is good enough. Imagine that you are flipping a coin over and over until you get 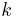$k$ heads. Although this could take a long time, on average only 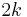$2k$ flips are required, and the chance that you won't get 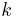$k$ heads after 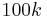$100k$ flips is highly improbable. By the same argument, quicksort's recursion will terminate on average at a call depth of only 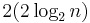$2(2\log_2 n)$ . But if its average call depth is 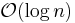$\mathcal{O}(\log n)$ , and each level of the call tree processes at most 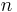$n$ elements, the total amount of work done on average is the product, 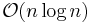$\mathcal{O}(n \log n)$ . Note that the algorithm does not have to verify that the pivot is in the middle half - if we hit it any constant fraction of the times, that is enough for the desired complexity.

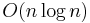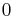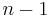The outline of a formal proof of the $O(n \log n)$ expected time complexity follows. Assume that there are no duplicates as duplicates could be handled with linear time pre- and post-processing, or considered cases easier than the analyzed. Choosing a pivot, uniformly at random from $0$ to $n-1$ , is then equivalent to choosing the size of one particular partition, uniformly at random from 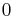$0$ to $n-1$ . 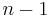With this observation, the continuation of the proof is analogous to the one given in the average complexity section.

Average complexity

Even if pivots aren't chosen randomly, quicksort still requires only 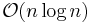$\mathcal{O}(n \log n)$ time over all possible permutations of its input. Because this average is simply the sum of the times over all permutations of the input divided by 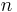$n$ factorial, it's equivalent to choosing a random permutation of the input. When we do this, the pivot choices are essentially random, leading to an algorithm with the same running time as randomized quicksort.

More precisely, the average number of comparisons over all permutations of the input sequence can be estimated accurately by solving the recurrence relation:

$C(n) = n - 1 + \frac{1}{n} \sum_{i=0}^{n-1} (C(i)+C(n-i-1)) = 2n \ln n = 1.39n \log_2 n.$

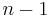Here, $n-1$ is the number of comparisons the partition uses. Since the pivot is equally likely to fall anywhere in the sorted list order, the sum is averaging over all possible splits.

This means that, on average, quicksort performs only about 39% worse than the ideal number of comparisons, which is its best case. In this sense it is closer to the best case than the worst case. This fast average runtime is another reason for quicksort's practical dominance over other sorting algorithms.

Space complexity

The space used by quicksort depends on the version used.

Quicksort has a space complexity of 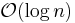$\mathcal{O}(\log n)$ , even in the worst case, when it is carefully implemented ensuring the following two properties:

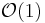in-place partitioning is used. This requires $\mathcal{O}(1)$ .
After partitioning, the partition with the fewest elements is (recursively) sorted first, requiring at most 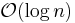$\mathcal{O}(\log n)$ space. Then the other partition is sorted using tail recursion or iteration. This idea, as discussed above, was described by R. Sedgewick). ^[2]^[3]

The version of quicksort with in-place partitioning uses only constant additional space before making any recursive call. However, if it has made 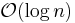$\mathcal{O}(\log n)$ nested recursive calls, it needs to store a constant amount of information from each of them. Since the best case makes at most 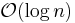$\mathcal{O}(\log n)$ nested recursive calls, it uses 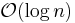$\mathcal{O}(\log n)$ space. The worst case makes 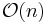$\mathcal{O}(n)$ nested recursive calls, and so needs 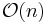$\mathcal{O}(n)$ space; Sedgewick's improved version using tail recursion requires 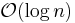$\mathcal{O}(\log n)$ space in the worst case.

We are eliding a small detail here, however. If we consider sorting arbitrarily large lists, we have to keep in mind that our variables like left and right can no longer be considered to occupy constant space; it takes 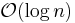$\mathcal{O}(\log n)$ bits to index into a list of 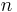$n$ items. Because we have variables like this in every stack frame, in reality quicksort requires 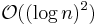$\mathcal{O}((\log n)^2)$ bits of space in the best and average case and 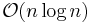$\mathcal{O}(n \log n)$ space in the worst case. This isn't too terrible, though, since if the list contains mostly distinct elements, the list itself will also occupy 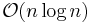$\mathcal{O}(n \log n)$ bits of space.

The not-in-place version of quicksort uses 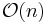$\mathcal{O}(n)$ space before it even makes any recursive calls. In the best case its space is still limited to 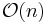$\mathcal{O}(n)$ , because each level of the recursion uses half as much space as the last, and

$\sum_{i=0}^{\infty} \frac{n}{2^i} = 2n.$

Its worst case is dismal, requiring

$\sum_{i=0}^n (n-i+1) = \mathcal{O}(n^2)$

space, far more than the list itself. If the list elements are not themselves constant size, the problem grows even larger; for example, if most of the list elements are distinct, each would require about 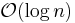$\mathcal{O}(\log n)$ bits, leading to a best-case 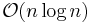$\mathcal{O}(n \log n)$ and worst-case 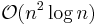$\mathcal{O}(n^2 \log n)$ space requirement.

Selection-based pivoting

A selection algorithm chooses the kth smallest of a list of numbers; this is an easier problem in general than sorting. One simple but effective selection algorithm works nearly in the same manner as quicksort, except that instead of making recursive calls on both sublists, it only makes a single tail-recursive call on the sublist which contains the desired element. This small change lowers the average complexity to linear or 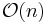$\mathcal{O}(n)$ time, and makes it an in-place algorithm. A variation on this algorithm brings the worst-case time down to 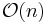$\mathcal{O}(n)$ (see selection algorithm for more information).

Conversely, once we know a worst-case 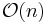$\mathcal{O}(n)$ selection algorithm is available, we can use it to find the ideal pivot (the median) at every step of quicksort, producing a variant with worst-case 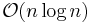$\mathcal{O}(n \log n)$ running time. In practical implementations, however, this variant is considerably slower on average.

Another variant is to choose the Median of Medians as the pivot element instead of the median itself for partitioning the elements. While maintaining the asymptotically optimal run time complexity of 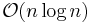$\mathcal{O}(n \log n)$ (by preventing worst case partitions), it is also considerably faster than the variant that chooses the median as pivot.

Variants

There are three well known variants of quicksort:

Balanced quicksort: choose a pivot likely to represent the middle of the values to be sorted, and then follow the regular quicksort algorithm.
External quicksort: The same as regular quicksort except the pivot is replaced by a buffer. First, read the M/2 first and last elements into the buffer and sort them. Read the next element from the beginning or end to balance writing. If the next element is less than the least of the buffer, write it to available space at the beginning. If greater than the greatest, write it to the end. Otherwise write the greatest or least of the buffer, and put the next element in the buffer. Keep the maximum lower and minimum upper keys written to avoid resorting middle elements that are in order. When done, write the buffer. Recursively sort the smaller partition, and loop to sort the remaining partition.
Three-way radix quicksort (also called multikey quicksort): is a combination of radix sort and quicksort. Pick an element from the array (the pivot) and consider the first character (key) of the string (multikey). Partition the remaining elements into three sets: those whose corresponding character is less than, equal to, and greater than the pivot's character. Recursively sort the "less than" and "greater than" partitions on the same character. Recursively sort the "equal to" partition by the next character (key).

Comparison with other sorting algorithms

Quicksort is a space-optimized version of the binary tree sort. Instead of inserting items sequentially into an explicit tree, quicksort organizes them concurrently into a tree that is implied by the recursive calls. The algorithms make exactly the same comparisons, but in a different order.

The most direct competitor of quicksort is heapsort. Heapsort's worst-case running time is always 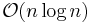$\mathcal{O}(n \log n)$ . But, heapsort is assumed to be in average somewhat slower than quicksort. This is still debated and in research, with some publications indicating the opposite.^[10]^[11] In Quicksort remains the chance of worst case performance except in the introsort variant, which switches to heapsort when a bad case is detected. If it is known in advance that heapsort is going to be necessary, using it directly will be faster than waiting for introsort to switch to it.

Quicksort also competes with mergesort, another recursive sort algorithm but with the benefit of worst-case 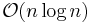$\mathcal{O}(n \log n)$ running time. Mergesort is a stable sort, unlike quicksort and heapsort, and can be easily adapted to operate on linked lists and very large lists stored on slow-to-access media such as disk storage or network attached storage. Although quicksort can be written to operate on linked lists, it will often suffer from poor pivot choices without random access. The main disadvantage of mergesort is that, when operating on arrays, it requires 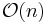$\mathcal{O}(n)$ auxiliary space in the best case, whereas the variant of quicksort with in-place partitioning and tail recursion uses only 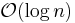$\mathcal{O}(\log n)$ space. (Note that when operating on linked lists, mergesort only requires a small, constant amount of auxiliary storage.)

Bucket sort with two buckets is very similar to quicksort; the pivot in this case is effectively the value in the middle of the value range, which does well on average for uniformly distributed inputs.

Notes

↑ "An Interview with C.A.R. Hoare". Communications of the ACM, March 2009 ("premium content"). http://cacm.acm.org/magazines/2009/3/21782-an-interview-with-car-hoare/fulltext.
↑ ^2.0 ^2.1 R. Sedgewick, Algorithms in C, Parts 1-4: Fundamentals, Data Structures, Sorting, Searching, 3rd Edition, Addison-Wesley
↑ ^3.0 ^3.1 R. Sedgewick, Implementing quicksort programs, Comm. ACM, 21(10):847-857, 1978.
↑ qsort.c in GNU libc: [1], [2]
↑ http://home.tiscalinet.ch/t_wolf/tw/ada95/sorting/index.html
↑ http://www.ugrad.cs.ubc.ca/~cs260/chnotes/ch6/Ch6CovCompiled.html
↑ R.Miller, L.Boxer, Algorithms Sequential & Parallel, A Unified Approach, Prentice Hall, NJ, 2006
↑ David M. W. Powers, Parallelized Quicksort with Optimal Speedup, Proceedings of International Conference on Parallel Computing Technologies. Novosibirsk. 1991.
↑ M. D. McIlroy. A Killer Adversary for Quicksort. Software Practice and Experience: vol.29, no.4, 341–344. 1999. At Citeseer
↑ Hsieh, Paul (2004). "Sorting revisited.". www.azillionmonkeys.com. http://www.azillionmonkeys.com/qed/sort.html. Retrieved 2010-04-26.
↑ MacKay, David (2005-12-01). "Heapsort, Quicksort, and Entropy". users.aims.ac.za/~mackay. http://users.aims.ac.za/~mackay/sorting/sorting.html. Retrieved 2010-04-26.

References

Brian C. Dean, "A Simple Expected Running Time Analysis for Randomized 'Divide and Conquer' Algorithms." Discrete Applied Mathematics 154(1): 1-5. 2006.
Hoare, C. A. R. "Partition: Algorithm 63," "Quicksort: Algorithm 64," and "Find: Algorithm 65." Comm. ACM 4(7), 321-322, 1961
Hoare, C. A. R. "Quicksort." Computer Journal 5 (1): 10-15. (1962). (Reprinted in Hoare and Jones: Essays in computing science, 1989.)
David Musser. Introspective Sorting and Selection Algorithms, Software Practice and Experience vol 27, number 8, pages 983-993, 1997
Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 113–122 of section 5.2.2: Sorting by Exchanging.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 7: Quicksort, pp. 145–164.
A. LaMarca and R. E. Ladner. "The Influence of Caches on the Performance of Sorting." Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, 1997. pp. 370-379.
Faron Moller. Analysis of Quicksort. CS 332: Designing Algorithms. Department of Computer Science, Swansea University.
Conrado Martínez and Salvador Roura, Optimal sampling strategies in quicksort and quickselect. SIAM J. Computing 31(3):683-705, 2001.
Jon L. Bentley and M. Douglas McIlroy, Engineering a Sort Function, Software—Practice and Experience, Vol. 23(11), 1249–1265, 1993

External links

Animated Sorting Algorithms: Quick Sort – graphical demonstration and discussion of quick sort
Quick Sort in C++
Animated Sorting Algorithms: 3-Way Partition Quick Sort – graphical demonstration and discussion of 3-way partition quick sort
Interactive Tutorial for Quicksort
Analyze Quicksort in an online Javascript IDE
Javascript Quicksort and Bubblesort
Quicksort applet with "level-order" recursive calls to help improve algorithm analysis
Multidimensional quicksort in Java
Literate implementations of Quicksort in various languages on LiteratePrograms
Quicksort tutorial with illustrated examples
A colored graphical Java applet which allows experimentation with initial state and shows statistics
Quicksort illustrated explanation. Java and C++ implementations.

Sorting algorithms

Theory	Computational complexity theory · Big O notation · Total order · Lists · Stability · Comparison sort

Exchange sorts	Bubble sort · Cocktail sort · Odd-even sort · Comb sort · Gnome sort · Quicksort

Selection sorts	Selection sort · Heapsort · Smoothsort · Cartesian tree sort · Tournament sort · Cycle sort

Insertion sorts	Insertion sort · Shell sort · Tree sort · Library sort · Patience sorting

Merge sorts	Merge sort · Polyphase merge sort · Strand sort · Timsort

Non-comparison sorts	Bead sort · Bucket sort · Burstsort · Counting sort · Pigeonhole sort · Proxmap sort · Radix sort

Others	Topological sorting · Sorting network · Bitonic sorter · Batcher odd-even mergesort · Pancake sorting

Ineffective/humorous sorts	Bogosort · Stooge sort