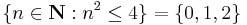Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.
In logic, quantification is the binding of a variable ranging over a domain of discourse. The variable thereby becomes bound by an operator called a quantifier. Academic discussion of quantification refers more often to this meaning of the term than the preceding one.
In grammar, a quantifier is a type of determiner, such as all or many, that indicates quantity. These items have been argued to correspond to logical quantifiers at the semantic level.
Contents |
Natural language
All known human languages make use of quantification (Wiese 2004). For example, in English:
- Every glass in my recent order was chipped.
- Some of the people standing across the river have white armbands.
- Most of the people I talked to didn't have a clue who the candidates were.
- Everyone in the waiting room had at least one complaint against Dr. Ballyhoo.
- There was somebody in his class that was able to correctly answer every one of the questions I submitted.
- A lot of people are smart.
The words in italics are quantifiers. Most quantifiers are grammatically classed as determiners.
There exists no simple way of reformulating any one of these expressions as a conjunction or disjunction of sentences, each a simple predicate of an individual such as That wine glass was chipped. These examples also suggest that the construction of quantified expressions in natural language can be syntactically very complicated. Fortunately, for mathematical assertions, the quantification process is syntactically more straightforward.
The study of quantification in natural languages is much more difficult than the corresponding problem for formal languages. This comes in part from the fact that the grammatical structure of natural language sentences may conceal the logical structure. Moreover, mathematical conventions strictly specify the range of validity for formal language quantifiers; for natural language, specifying the range of validity requires dealing with non-trivial semantic problems. For example the sentence ″Someone gets mugged in New York every 10 minutes″ does not identify whether it is the same person getting mugged every 10 minutes.
Montague grammar gives a novel formal semantics of natural languages. Its proponents argue that it provides a much more natural formal rendering of natural language than the traditional treatments of Frege, Russell and Quine.
Logic
In language and logic, quantification is a construct that specifies the quantity of specimens in the domain of discourse that apply to (or satisfy) an open formula. For example, in arithmetic, it allows the expression of the statement that every natural number has a successor. A language element which generates a quantification is called a quantifier. The resulting expression is a quantified expression; and the expression is said to be quantified over the predicate or function expression whose free variable is bound by the quantifier. Quantification is used in both natural languages and formal languages. Examples of quantifiers in English are for all, for some, many, few, a lot, and no. In formal languages, quantification is a formula constructor that produces new formulas from old ones. The semantics of the language specifies how the constructor is interpreted as an extent of validity.
The two fundamental kinds of quantification in predicate logic are universal quantification and existential quantification. The traditional symbol for the universal quantifier "all" is "∀", an inverted letter "A", and for the existential quantifier "exists" is "∃", a rotated letter "E". These quantifiers have been generalized beginning with the work of Mostowski and Lindström. See generalized quantifier and Lindström quantifier for further details.
Mathematics
Consider the following statement:
- 1·2 = 1 + 1, and 2·2 = 2 + 2, and 3 · 2 = 3 + 3, ...., and n · 2 = n + n, etc.
This has the appearance of an infinite conjunction of propositions. From the point of view of formal languages this is immediately a problem, since syntax rules are expected to generate finite objects. The example above is fortunate in that there is a procedure to generate all the conjuncts. However, if an assertion were to be made about every irrational number, there would be no way to enumerate all the conjuncts, since irrationals cannot be enumerated. A succinct formulation which avoids these problems uses universal quantification:
- For any natural number n, n·2 = n + n.
A similar analysis applies to the disjunction,
- 4 is not the sum of two primes, or 6 is not the sum of two primes, or 8 is not the sum of two primes, ...
which can be rephrased using existential quantification:
- For some even natural number n, where n is greater than 2, n is not the sum of two primes.
Goldbach's conjecture is that this statement is false, that is, that every even natural number greater than 2 is the sum of two primes.
It is possible to devise abstract algebras whose models include formal languages with quantification, but progress has been slow and interest in such algebra has been limited. Three approaches have been devised to date:
- Relation algebra, invented by DeMorgan, and developed by Ernst Schroder, Tarski, and Tarski's students. Relation algebra cannot represent any formula with quantifiers nested more than three deep. Surprisingly, the models of relation algebra include the axiomatic set theory ZFC and Peano arithmetic;
- Cylindric algebra, devised by Tarski, Henkin, and others;
- The polyadic algebra of Paul Halmos.
Notation
The traditional symbol for the universal quantifier is "∀", an inverted letter "A", which stands for the word "all"; in other schools, a  is used instead. The corresponding symbol for the existential quantifier is "∃", a rotated letter "E", which stands for the word "exists". Other schools use the symbol
is used instead. The corresponding symbol for the existential quantifier is "∃", a rotated letter "E", which stands for the word "exists". Other schools use the symbol  instead. Correspondingly, quantified expressions are constructed as follows,
instead. Correspondingly, quantified expressions are constructed as follows,
for a formula P. Variant notations include, for set X and set members x:
All of these variations also apply to universal quantification. Other variations for the universal quantifier are
Some versions of the notation explicitly mention the range of quantification. The range of quantification must always be specified; for a given mathematical theory, this can be done in several ways:
- Assume a fixed domain of discourse for every quantification, as is done in Zermelo–Fraenkel set theory,
- Fix several domains of discourse in advance and require that each variable have a declared domain, which is the type of that variable. This is analogous to the situation in statically typed computer programming languages, where variables have declared types.
- Mention explicitly the range of quantification, perhaps using a symbol for the set of all objects in that domain or the type of the objects in that domain.
One can use any variable as a quantified variable in place of any other, under certain restrictions in which variable capture does not occur. Even if the notation uses typed variables, variables of that type may be used.
Informally or in natural language, the "∀x" or "∃x" might appear after or in the middle of P(x). Formally, however, the phrase that introduces the dummy variable is placed in front.
Mathematical formulas mix symbolic expressions for quantifiers, with natural language quantifiers such as
- For any natural number x, ....
- There exists an x such that ....
- For at least one x.
Keywords for uniqueness quantification include:
- For exactly one natural number x, ....
- There is one and only one x such that ....
Further, x may be replaced by a pronoun. For example,
- For any natural number, its product with 2 equals to its sum with itself
- Some natural number is prime.
Nesting
Consider the following statement:
- For any natural number n, there is a natural number s such that s = n × n.
This is clearly true; it just asserts that every natural number has a square.
The meaning of the assertion in which the quantifiers are turned around is different:
- There is a natural number s such that for any natural number n, s = n × n.
This is clearly false; it asserts that there is a single natural number s that is at once the square of every natural number.
This illustrates that the order of alternation of quantifiers is critical to meaning.
A less trivial example is the important concept of uniform continuity from analysis, which differs from the more familiar concept of pointwise continuity only by an exchange in the positions of two quantifiers. To illustrate this, let f be a real-valued function on R.
- A: Pointwise continuity of f on R:
interchanging the universal quantifiers over the braces, this is the same as
- A': Pointwise continuity of f on R:
This differs from
- B: Uniform continuity of f on R:
by interchanging the existential and universal quantifiers over the braces in A'.
Ambiguity is avoided with the quantifiers in front:
 A:
A: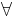 B: C – unambiguous
B: C – unambiguous- there is an A such that
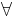 B: C – unambiguous
B: C – unambiguous - there is an A such that for all B, C – unambiguous, provided that the separation between B and C is clear
- there is an A such that C for all B – it is often clear that what is meant is
-
- there is an A such that (C for all B)
- but it could be interpreted as
- (there is an A such that C) for all B
- there is an A such that C
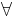 B – suggests more strongly that the first is meant; this may be reinforced by the layout, for example by putting "C
B – suggests more strongly that the first is meant; this may be reinforced by the layout, for example by putting "C 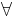 B" on a new line.
B" on a new line.
Range of quantification
Every quantification involves one specific variable and a domain of discourse or range of quantification of that variable. The range of quantification specifies the set of values that the variable takes. In the examples above, the range of quantification is the set of natural numbers. Specification of the range of quantification allows us to express the difference between, asserting that a predicate holds for some natural number or for some real number. Expository conventions often reserve some variable names such as "n" for natural numbers and "x" for real numbers, although relying exclusively on naming conventions cannot work in general since ranges of variables can change in the course of a mathematical argument.
A more natural way to restrict the domain of discourse uses guarded quantification. For example, the guarded quantification
- For some natural number n, n is even and n is prime
means
- For some even number n, n is prime.
In some mathematical theories a single domain of discourse fixed in advance is assumed. For example, in Zermelo–Fraenkel set theory, variables range over all sets. In this case, guarded quantifiers can be used to mimic a smaller range of quantification. Thus in the example above to express
- For any natural number n, n·2 = n + n
in Zermelo–Fraenkel set theory, it can be said
- For any n, if n belongs to N, then n·2 = n + n,
where N is the set of all natural numbers.
Formal semantics
Mathematical Semantics is the application of mathematics to study the meaning of expressions in a formal language. It has three elements: A mathematical specification of a class of objects via syntax, a mathematical specification of various semantic domains and the relation between the two, which is usually expressed as a function from syntactic objects to semantic ones. This article only addresses the issue of how quantifier elements are interpreted.
Given a model theoretical logical framework, the syntax of a formula can be given by a syntax tree. Quantifiers have scope and a variable x is free if it is not within the scope of a quantification for that variable. Thus in
the occurrence of both x and y in C(y,x) is free.

An interpretation for first-order predicate calculus assumes as given a domain of individuals X. A formula A whose free variables are x1, ..., xn is interpreted as a boolean-valued function F(v1, ..., vn) of n arguments, where each argument ranges over the domain X. Boolean-valued means that the function assumes one of the values T (interpreted as truth) or F (interpreted as falsehood). The interpretation of the formula
is the function G of n-1 arguments such that G(v1, ...,vn-1) = T if and only if F(v1, ..., vn-1, w) = T for every w in X. If F(v1, ..., vn-1, w) = F for at least one value of w, then G(v1, ...,vn-1) = F. Similarly the interpretation of the formula
is the function H of n-1 arguments such that H(v1, ...,vn-1) = T if and only if F(v1, ...,vn-1, w) = T for at least one w and H(v1, ..., vn-1) = F otherwise.
The semantics for uniqueness quantification requires first-order predicate calculus with equality. This means there is given a distinguished two-placed predicate "="; the semantics is also modified accordingly so that "=" is always interpreted as the two-place equality relation on X. The interpretation of
then is the function of n-1 arguments, which is the logical and of the interpretations of
Paucal, multal and other degree quantifiers
None of the quantifiers previously discussed apply to a quantification such as
- There are many integers n < 100, such that n is divisible by 2 or 3 or 5.
One possible interpretation mechanism can obtained as follows: Suppose that in addition to a semantic domain X, we have given a probability measure P defined on X and cutoff numbers 0 < a ≤ b ≤ 1. If A is a formula with free variables x1,...,xn whose interpretation is the function F of variables v1,...,vn then the interpretation of
is the function of v1,...,vn-1 which is T if and only if
and F otherwise. Similarly, the interpretation of
is the function of v1,...,vn-1 which is F if and only if
and T otherwise. See Fubini's theorem for more discussion of the measurability of the interpretation functions.
Other quantifiers
A few other quantifiers have been proposed over time. In particular, the solution quantifier,[1] noted § (section sign) and read "those". For example:
is read "those n in N such that n2 ≤ 4 are in {0,1,2}." The same construct is expressible in set-builder notation:
History
Term logic treats quantification in a manner that is closer to natural language, and also less suited to formal analysis. Aristotelian logic treated All, Some and No in the 1st century BC, in an account also touching on the alethic modalities.
Gottlob Frege, in his 1879 Begriffsschrift, was the first to employ a quantifier to bind a variable ranging over a domain of discourse and appearing in predicates. He would universally quantify a variable (or relation) by writing the variable over a dimple in an otherwise straight line appearing in his diagrammatic formulas. Frege did not devise an explicit notation for existential quantification, instead employing his equivalent of ~∀x~, or contraposition. Frege's treatment of quantification went largely unremarked until Bertrand Russell's 1903 Principles of Mathematics.
In work that culminated in Peirce (1885), Charles Sanders Peirce and his student Oscar Howard Mitchell independently invented universal and existential quantifiers, and bound variables. Peirce and Mitchell wrote Πx and Σx where we now write ∀x and ∃x. Peirce's notation can be found in the writings of Ernst Schroder, Leopold Loewenheim, Thoralf Skolem, and Polish logicians into the 1950s. Most notably, it is the notation of Kurt Gödel's landmark 1930 paper on the completeness of first-order logic, and 1931 paper on the incompleteness of Peano arithmetic.
Peirce's approach to quantification also influenced William Ernest Johnson and Giuseppe Peano, who invented yet another notation, namely (x) for the universal quantification of x and (in 1897) ∃x for the existential quantification of x. Hence for decades, the canonical notation in philosophy and mathematical logic was (x)P to express "all individuals in the domain of discourse have the property P," and "(∃x)P" for "there exists at least one individual in the domain of discourse having the property P." Peano, who was much better known than Peirce, in effect diffused the latter's thinking throughout Europe. Peano's notation was adopted by the Principia Mathematica of Whitehead and Russell, Quine, and Alonzo Church. In 1935, Gentzen introduced the ∀ symbol, by analogy with Peano's ∃ symbol. ∀ did not become canonical until the 1960s.
Around 1895, Peirce began developing his existential graphs, whose variables can be seen as tacitly quantified. Whether the shallowest instance of a variable is even or odd determines whether that variable's quantification is universal or existential. (Shallowness is the contrary of depth, which is determined by the nesting of negations.) Peirce's graphical logic has attracted some attention in recent years by those researching heterogeneous reasoning and diagrammatic inference.
Science
Some measure of the undisputed general importance of quantification in the natural sciences can be gleaned from the following comments: these are mere facts, but they are quantitative facts and the basis of science.[2] It seems to be held as universally true that the foundation of quantification is measurement.[3] There is little doubt that quantification provided a basis for the objectivity of science.[4] In ancient times, musicians and artists...rejected quantification, but merchants, by definition, quantified their affairs, in order to survive, made them visible on parchment and paper.[5] Any reasonable comparison between Aristotle and Galileo shows clearly that there can be no unique lawfulness discovered without detailed quantification.[6] Even today, universities use imperfect instruments called 'exams' to indirectly quantify something they call knowledge.[7] This meaning of quantification comes under the heading of pragmatics.
In quantitative analysis of behavior, evolutionary psychology and cognitive developmental psychology, quantification is studied as behavior.
See also
- Indefinite pronoun
- Quantifier elimination
References
- ↑ Hehner, Eric C. R., 2004, Practical Theory of Programming, 2nd edition, p. 28
- ↑ Cattell, James McKeen; and Farrand, Livingston (1896) "Physical and mental measurements of the students of Columbia University", The Psychological Review, Vol. 3, No. 6 (1896), pp. 618-648; p. 648 quoted in James McKeen Cattell (1860-1944) Psychologist, Publisher, and Editor.
- ↑ Wilks, Samuel Stanley (1961) "Some Aspects of Quantification in Science", Isis, Vol. 52, No. 2 (1961), pp. 135-142; p. 135
- ↑ Hong, Sungook (2004) "History of Science: Building Circuits of Trust", Science, Vol. 305, No. 5690 (10 September 2004), pp. 1569-1570
- ↑ Crosby, Alfred W. (1996) The Measure of Reality: Quantification and Western Society, Cambridge University Press, 1996, p. 201
- ↑ Langs, Robert J. (1987) "Psychoanalysis as an Aristotelian Science—Pathways to Copernicus and a Modern-Day Approach", Contemporary Psychoanalysis, Vol. 23 (1987), pp. 555-576
- ↑ Lynch, Aaron (1999) "Misleading Mix of Religion and Science," Journal of Memetics: Evolutionary Models of Information Transmission, Vol. 3, No. 1 (1999)
- Barwise, Jon; and Etchemendy, John, 2000. Language Proof and Logic. CSLI (University of Chicago Press) and New York: Seven Bridges Press. A gentle introduction to first-order logic by two first-rate logicians.
- Crosby, Alfred W. (1996) The Measure of Reality: Quantification and Western Society, 1250-1600. Cambridge University Press.
- Frege, Gottlob, 1879. Begriffsschrift. Translated in Jean van Heijenoort, 1967. From Frege to Gödel: A Source Book on Mathematical Logic, 1879-1931. Harvard University Press. The first appearance of quantification.
- Hilbert, David; and Ackermann, Wilhelm, 1950 (1928). Principles of Mathematical Logic. Chelsea. Translation of Grundzüge der theoretischen Logik. Springer-Verlag. The 1928 first edition is the first time quantification was consciously employed in the now-standard manner, namely as binding variables ranging over some fixed domain of discourse. This is the defining aspect of first-order logic.
- Peirce, C. S., 1885, "On the Algebra of Logic: A Contribution to the Philosophy of Notation, American Journal of Mathematics, Vol. 7, pp. 180–202. Reprinted in Kloesel, N. et al., eds., 1993. Writings of C. S. Peirce, Vol. 5. Indiana University Press. The first appearance of quantification in anything like its present form.
- Reichenbach, Hans, 1975 (1947). Elements of Symbolic Logic, Dover Publications. The quantifiers are discussed in chapters §18 "Binding of variables" through §30 "Derivations from Synthetic Premises".
- Westerståhl, Dag, 2001, "Quantifiers," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- Wiese, Heike, 2003. Numbers, language, and the human mind. Cambridge University Press. ISBN 0-521-83182-2.
External links
- Stanford Encyclopedia of Philosophy:
- "Classical Logic -- by Stewart Shapiro. Covers syntax, model theory, and metatheory for first order logic in the natural deduction style.
- "Generalized quantifiers" -- by Dag Westerståhl.
- Peters, Stanley; Westerståhl, Dag (2002). "Quantifiers."
|
|||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||

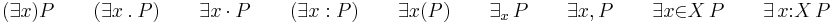
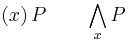
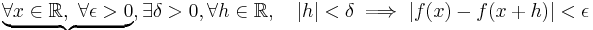
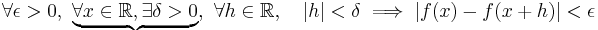




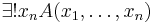



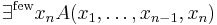

![\left [ \S n \in \mathbb{N} \quad n^2 \leq 4 \right ] = \left\{0, 1, 2\right\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6859bb71123d71a27cf0899a82d1f392.png)