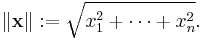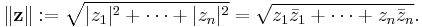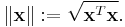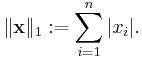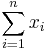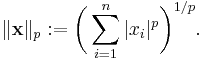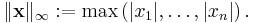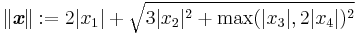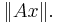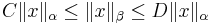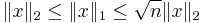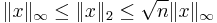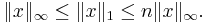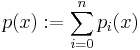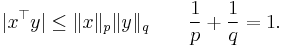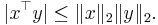Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors.

A simple example is the 2-dimensional Euclidean space R² equipped with the Euclidean norm. Elements in this vector space (e.g., (3, 7) ) are usually drawn as arrows in a 2-dimensional cartesian coordinate system starting at the origin (0, 0). The Euclidean norm assigns to each vector the length of its arrow. Because of this, the Euclidean norm is often known as the magnitude.

A vector space with a norm is called a normed vector space. Similarly, a vector space with a seminorm is called a seminormed vector space.

1 Definition
- 1.1 Notation
2 Examples
3 Properties
4 Classification of seminorms: Absolutely convex absorbing sets
5 See also
6 Notes
7 References

Definition

Given a vector space V over a subfield F of the complex numbers, including imaginary numbers or real numbers, a norm on V is a function 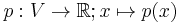$p:V\to\mathbb{R}; x\mapsto{}p(x)$ with the following properties:^[1]

For all a in F and all u and v in V,

p(a v) = |a| p(v), (positive homogeneity or positive scalability)
p(u + v) ≤ p(u) + p(v) (triangle inequality or subadditivity).
p(v) = 0 if and only if v is the zero vector (positive definiteness).

A simple consequence of the first two axioms, positive homogeneity and the triangle inequality, is p(0) = 0 and thus

p(v) ≥ 0 (positivity).

A seminorm is a norm with the requirement of positive definiteness removed.

Although every vector space is seminormed (e.g., with the trivial seminorm in the Examples section below), it may be not normed. Every vector space V with seminorm p(v) induces a normed space V/W, called the quotient space, where W is the subspace of V consisting of all vectors v in V with p(v) = 0. The induced norm on V/W is clearly well-defined and is given by:

p(W+v) = p(v).

A topological vector space is called normable (seminormable) if the topology of the space can be induced by a norm (seminorm).

Notation

The norm of a vector v is usually denoted ||v||, and sometimes |v|. However, the latter notation is generally discouraged, because it is also used to denote the absolute value of scalars and the determinant of matrices.

Examples

All norms are seminorms.
The trivial seminorm, with p(x) = 0 for all x in V.
The absolute value is a norm on the real numbers.
Every linear form f on a vector space defines a seminorm by x → |f(x)|.

Euclidean norm

On Rⁿ, the intuitive notion of length of the vector x = [x₁, x₂, ..., x_n] is captured by the formula

$\|\mathbf{x}\|�:= \sqrt{x_1^2 + \cdots + x_n^2}.$

This gives the ordinary distance from the origin to the point x, a consequence of the Pythagorean theorem. The Euclidean norm is by far the most commonly used norm on Rⁿ, but there are other norms on this vector space as will be shown below. However all these norms are equivalent in the sense that they all define the same topology.

On Cⁿ the most common norm is

$\|\mathbf{z}\|�:= \sqrt{|z_1|^2 + \cdots + |z_n|^2}= \sqrt{z_1 \bar z_1 + \cdots + z_n \bar z_n}.$

In each case we can also express the norm as the square root of the inner product of the vector and itself:

$\|\mathbf{x}\|�:= \sqrt{\mathbf{x}^{T}\mathbf{x}}.$

The Euclidean norm is also called the Euclidean length, and the L² distance, ℓ² distance, L² norm, or ℓ² norm; see L^p space.

The set of vectors whose Euclidean norm is a given constant forms the surface of an n-sphere, with n+1 being the dimension of the Euclidean space.

Euclidean norm of a complex number

The Euclidian norm of a complex number is the absolute value (also called the modulus) of it, if the complex plane is identified with the Euclidean plane R². This identification of the complex number x + iy as a vector in the Euclidian plane, makes the quantity 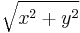$\sqrt{x^2 +y^2}$ (as first suggested by Euler) the Euclidian norm associated with the complex number.

Taxicab norm or Manhattan norm

Main article: Taxicab geometry

$\|\mathbf{x}\|_1�:= \sum_{i=1}^{n} |x_i|.$

The name relates to the distance a taxi has to drive in a rectangular street grid to get from the origin to the point x.

The set of vectors whose 1-norm is a given constant forms the surface of a cross polytope of dimension equivalent to that of the norm minus 1. The Taxicab norm is also called the L¹ norm. The distance derived from this norm is called the Manhattan distance or L₁ distance.

In contrast,

$\sum_{i=1}^{n} x_i$

is not a norm because it may yield negative results.

p-norm

Main article: L^p space

Let p ≥ 1 be a real number.

$\|\mathbf{x}\|_p�:= \bigg( \sum_{i=1}^n |x_i|^p \bigg)^{1/p}.$

Note that for p = 1 we get the taxicab norm, for p = 2 we get the Euclidean norm, and for p = $\infty$ we get the infinity norm or maximum norm.

This definition is still of some interest for 0 < p < 1, but the resulting function does not define a norm,^[2] because it violates the triangle inequality. What is true, even in the measurable analog, is that the corresponding L^p class is a vector space, and it is also true that the function 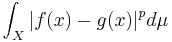$\int_X|f(x)-g(x)|^p d\mu$ (without p-th rooth) defines a distance that makes L^p(X) into a complete metric topological vector space. However, outside trivial cases, this topological vector space is not locally convex and has no continuous nonzero linear forms.

Maximum norm (special case of: infinity norm, uniform norm, or supremum norm)

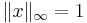
$\|x\|_\infty = 1$

$\|\mathbf{x}\|_\infty�:= \max \left(|x_1|, \ldots ,|x_n| \right).$

The set of vectors whose infinity norm is a given constant, c, forms the surface of a hypercube with edge length 2c.

Zero norm

In the machine learning and optimization literature, one often finds reference to the zero norm. The zero norm of x is simply the number of non-zero elements of x. It derives its name as being the limit of p-norms as p approaches 0. Despite its name, the zero norm is not a true norm; in particular, it is not positive homogeneous. Such a norm can be defined over arbitrary fields (besides the fields of complex numbers). In the context of the information theory, it is often called the Hamming distance in the case of the 2-element GF(2) field.

Other norms

Other norms on Rⁿ can be constructed by combining the above; for example

$\|\emph{\textbf{x}}\|�:= 2|x_1| + \sqrt{3|x_2|^2 + \max(|x_3|,2|x_4|)^2}$

is a norm on R⁴.

For any norm and any injective linear transformation A we can define a new norm of x, equal to

$\|Ax\|.$

In 2D, with A a rotation by 45° and a suitable scaling, this changes the taxicab norm into the maximum norm. In 2D, each A applied to the taxicab norm, up to inversion and interchanging of axes, gives a different unit ball: a parallelogram of a particular shape, size and orientation. In 3D this is similar but different for the 1-norm (octahedrons) and the maximum norm (prisms with parallelogram base).

All the above formulas also yield norms on Cⁿ without modification.

Infinite dimensional case

The generalization of the above norms to an infinite number of components leads to the L^p spaces, with norms

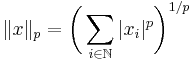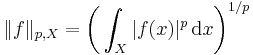
$\|x\|_p = \bigg(\sum_{i\in\mathbb N}|x_i|^p\bigg)^{1/p}$ resp. $\|f\|_{p,X} = \bigg(\int_X|f(x)|^p\,\mathrm dx\bigg)^{1/p}$

(for complex-valued sequences x resp. functions f defined on 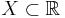$X\subset\mathbb R$ ), which can be further generalized (see Haar measure).

Any inner product induces in a natural way the norm 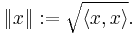$\|x\|�:= \sqrt{\langle x,x\rangle}.$

Other examples of infinite dimensional normed vector spaces can be found in the Banach space article.

Properties

Illustrations of unit circles in different norms.

The concept of unit circle (the set of all vectors of norm 1) is different in different norms: for the 1-norm the unit circle in R² is a square, for the 2-norm (Euclidean norm) it is the well-known unit circle, while for the infinity norm it is a different square. For any p-norm it is a superellipse (with congruent axes). See the accompanying illustration. Note that due to the definition of the norm, the unit circle is always convex and centrally symmetric (therefore, for example, the unit ball may be a rectangle but cannot be a triangle).

In terms of the vector space, the seminorm defines a topology on the space, and this is a Hausdorff topology precisely when the seminorm can distinguish between distinct vectors, which is again equivalent to the seminorm being a norm. The topology thus defined (by either a norm or a seminorm) can be understood either in terms of sequences or open sets. 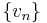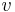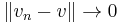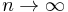A sequence of vectors $\{v_n\}$ is said to converge in norm to $v$ if $\|v_n - v\| \rightarrow 0$ as $n \to \infty$ . Equivalently, the topology consists of all sets that can be represented as a union of open balls.

Two norms ||•||_α and ||•||_β on a vector space V are called equivalent if there exist positive real numbers C and D such that

$C\|x\|_\alpha\leq\|x\|_\beta\leq D\|x\|_\alpha$

for all x in V. For instance, on 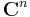$\mathbf{C}^n$ :

$\|x\|_2\le\|x\|_1\le\sqrt{n}\|x\|_2$

$\|x\|_\infty\le\|x\|_2\le\sqrt{n}\|x\|_\infty$

$\|x\|_\infty\le\|x\|_1\le n\|x\|_\infty.$

If the vector space is a finite-dimensional real/complex one, all norms are equivalent. If not, some norms are not.

Equivalent norms define the same notions of continuity and convergence and for many purposes do not need to be distinguished. To be more precise the uniform structure defined by equivalent norms on the vector space is uniformly isomorphic.

Every (semi)-norm is a sublinear function, which implies that every norm is a convex function. As a result, finding a global optimum of a norm-based objective function is often tractable.

Given a finite family of seminorms p_i on a vector space the sum

$p(x):=\sum_{i=0}^n p_i(x)$

is again a seminorm.

For any norm p on a vector space V, we have that for all u and v ∈ V:

p(u ± v) ≥ | p(u) − p(v) |

For the l^p norms, we have the Hölder's inequality^[3]

$|x^\top y|\le\| x\|_p\|y\|_q\qquad \frac{1}{p}+\frac{1}{q}=1.$

A special case of the above property is the Cauchy-Schwarz inequality:^[3]

$|x^\top y|\le\|x\|_2\|y\|_2.$

Classification of seminorms: Absolutely convex absorbing sets

All seminorms on a vector space V can be classified in terms of absolutely convex absorbing sets in V. To each such set, A, corresponds a seminorm p_A called the gauge of A, defined as

p_A(x) := inf{α : α > 0, x ∈ α A}

with the property that

{x : p_A(x) < 1} ⊆ A ⊆ {x : p_A(x) ≤ 1}.

Conversely:

Any locally convex topological vector space has a local basis consisting of absolutely convex sets. A common method to construct such a basis is to use a separating family (p) of seminorms p: the collection of all finite intersections of sets {p<1/n} turns the space into a locally convex topological vector space so that every p is continuous.

A such method is used to design weak and weak* topologies.

norm case:

Suppose now that (p) contains a single p: since (p) is separating, p is a norm, and A={p<1} is its open unit ball. Then A is an absolutely convex bounded neighbourhood of 0, and p = p_A is continuous.

The converse is due to Kolmogorov: any locally convex and locally bounded topological vector space is normable. Precisely:

If V is an absolutely convex bounded neighbourhood of 0, the gauge g_V (so that V={g_V <1}) is a norm.

Notes

↑ Eduard Prugovec̆ki (1981). Quantum mechanics in Hilbert space (2nd ed.). Academic Press. p. 20. ISBN 012566060X. http://books.google.com/books?id=GxmQxn2PF3IC&pg=PA20.
↑ Except in R¹, where it coincides with the Euclidean norm, and R⁰, where it is trivial.
↑ ^3.0 ^3.1 Golub, Gene; Charles F. Van Loan (1996). Matrix Computations - Third Edition. Baltimore: The Johns Hopkins University Press. p. 53. ISBN 0-8018-5413-X.

References

Bourbaki, N. (1987). Topological Vector Spaces, Chapters 1-5. Elements of Mathematics. Springer. ISBN 3-540-13627-4.