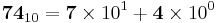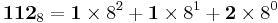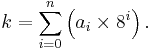Octal

Numeral systems by culture
Hindu-Arabic numerals
Western Arabic Eastern Arabic Indian family Burmese	Khmer Mongolian Thai
East Asian numerals
Chinese Japanese Suzhou	Korean Vietnamese Counting rods
Alphabetic numerals
Abjad Armenian Āryabhaṭa Cyrillic	Ge'ez Greek (Ionian) Hebrew
Other systems
Aegean Attic Babylonian Brahmi Egyptian Etruscan	Inuit Mayan Quipu Roman Sumerian Urnfield
List of numeral system topics
Positional systems by base
Decimal (10)
1, 2, 3, 4, 5, 6, 8, 12, 16, 20, 30, 36, 60 more…

The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Numerals can be made from binary numerals by grouping consecutive binary digits into groups of three (starting from the right). For example, the binary representation for decimal 74 is 1001010, which can be grouped into (00)1 001 010 — so the octal representation is 112.

In decimal systems each decimal place is a base of 10. For example:

$\mathbf{74}_{10} = \mathbf{7} \times 10^1 + \mathbf{4} \times 10^0$

In octal numerals each place is a power with base 8. For example:

$\mathbf{112}_8 = \mathbf{1} \times 8^2 + \mathbf{1} \times 8^1 + \mathbf{2} \times 8^0$

By performing the calculation above in the familiar decimal system we see why 112 in octal is equal to 64+8+2 = 74 in decimal.

Octal is sometimes used in computing instead of hexadecimal.

1 Usage
2 Conversion between bases
3 See also
4 References
5 External links

Usage

By Native Americans

The Yuki language in California and the Pamean languages^[1] in Mexico have octal systems because the speakers count using the spaces between their fingers rather than the fingers themselves^[2].

In Europe

In 1716 King Charles XII of Sweden asked Emanuel Swedenborg to elaborate a number system based on 64 instead of 10. Swedenborg however argued that for people with less intelligence than the king such a big base would be too difficult and instead proposed 8 as the base. In 1718 Swedenborg wrote a manuscript, which has not been published: "En ny räknekonst som omväxlas vid talet 8 istället för det vanliga vid talet 10" ("A new arithmetic (or art of counting) which changes at the Number 8 instead of the usual at the Number 10"). The numbers 1-7 are there denoted by the consonants l, s, n, m, t, f, u (v) and zero by the vowel o. Thus 8 = "lo", 16 = "so", 24 = "no", 64 = "loo", 512 = "looo" etc. Numbers with consecutive consonants are pronounced with vowel sounds between in accordance with a special rule.^[3]

In fiction

The fictional alien felinoid species Kilrathi of the Wing Commander universe count in octal, since their paws have four toes instead of 5.
The Octospider species of Rama Revealed and the computer game RAMA use a colour code based on octal system, and its comprehension is a puzzle of the game scenario.
The Alterans from Stargate SG-1 use octal, even though they have ten fingers. It's possible that they count the gaps between each finger, ignore the thumb on each hand, or use the thumb as a base-2 counter (as on an abacus) allowing them to count up to 30 (24 in decimal) on their hands.
The satirist Tom Lehrer famously remarked in his song parodying new math that "base 8 is just like base 10... if you're missing two fingers."
In the first-person shooter Prey, numerical codes to open doors are entered in octal.
The Tau race in the Warhammer 40,000 universe use the octal system.
In The Beekeeper's Apprentice, Laurie R. King's first Sherlock Holmes pastiche featuring Mary Russell, base eight math played a key role in solving the mystery.
In the Star Wars universe, the alien race known as the Hutts counts in base eight, as they only have eight fingers.
In the Niven/Pournelle novell Footfall the pachydermoid Fithp count in base eight and tend to group things into powers of eight, such as military divisions of 64 soldiers. Niven's Kzin species also uses octal.
The Na'vi from Avatar use octal, since they have four fingers on each hand.

In computers

Octal is sometimes used in computing instead of hexadecimal, perhaps most often in modern times in conjunction with file permissions under Unix systems (see chmod). It has the advantage of not requiring any extra symbols as digits (the hexadecimal system is base-16 and therefore needs six additional symbols beyond 0–9). It is also used for digital displays.

At the time when octal originally became widely used in computing, systems such as the PDP-8, [ICL 1900]] and IBM mainframes employed 12-bit, 24-bit or 36-bit words. Octal was an ideal abbreviation of binary for these machines because eight (or twelve) digits could concisely display an entire machine word (each octal digit covering three binary digits). It also cut costs by allowing Nixie tubes, seven-segment displays, and calculators to be used for the operator consoles, where binary displays were too complex to use, decimal displays needed complex hardware to convert radixes, and hexadecimal displays needed to display more numerals.

All modern computing platforms, however, use 16-, 32-, or 64-bit words, further divided into eight-bit bytes. On such systems three octal digits per byte would be required, with the most significant octal digit representing two binary digits (plus one bit of the next significant byte, if any). Octal representation of a 16-bit word requires 6 digits, but the most significant octal digit represents (quite inelegantly) only one bit (0 or 1). This representation offers no way to easily read the most significant byte, because it's smeared over four octal digits. Therefore, hexadecimal is more commonly used in programming languages today, since two hexadecimal digits exactly specify one byte. Some platforms with a power-of-two word size still have instruction subwords that are more easily understood if displayed in octal; this includes the PDP-11 and Motorola 68000 family. The modern-day ubiquitous x86 architecture belongs to this category as well, but octal is rarely used on this platform.

In programming languages, octal literals are typically identified with a variety of prefixes, including the digit 0, the letters o or q, or the digit–letter combination 0o. For example, the literal 73 (base 8) might be represented as 073, o73, q73, or 0o73 in various languages. Newer languages have been abandoning the prefix 0, as decimal numbers are often represented with leading zeroes. The prefix q was introduced to avoid the prefix o being mistaken for a zero, while the prefix 0o was introduced to avoid starting a numerical literal with an alphabetic character (like o or q), since these might cause the literal to be confused with a variable name. The prefix 0o also follows the model set by the prefix 0x used for hexadecimal literals in the C language.^[4]^[5]^[6]

Octal numbers that are used in some programming languages (C, Perl, PostScript…) for textual/graphical representations of byte strings when some byte values (unrepresented in a code page, non-graphical, having special meaning in current context or otherwise undesired) have to be to escaped as \nnn. Octal representation of non-ASCII bytes may be particularly handy with UTF-8, where any start byte has octal value \3nn and any continuation byte has octal value \2nn.

Conversion between bases

Decimal to Octal conversion

Method of successive division by 8

To convert integer decimals to octal, divide the original number by the largest possible power of 8 and successively divide the remainders by successively smaller powers of 8 until the power is 1. The octal representation is formed by the quotients, written in the order generated by the algorithm.

For example, to convert 125₁₀ to octal:

125 / 8^2 = 1

125 − ((8^2)*1) = 61

61 / 8^1 = 7

61 − ((8^1)*7) = 5

Thus: 125₁₀ = 175₈

Another example:

900 / 8^3 = 1

900 − ((8^3)*1) = 388

388 / 8^2 = 6

388 − ((8^2)*6) = 4

4 / 8^1 = 0

4 − ((8^1)*0) = 4

4 / 8^0 = 4

Thus: 900₁₀ = 1604₈

Method of successive multiplication by 8

To convert a decimal fraction to octal, multiply by 8; the integer part of the result is the first digit of the octal fraction. Repeat the process with the fractional part of the result, until it is null or within acceptable error bounds.

Example: Convert 0.1640625 to octal:

0.1640625 x 8 = 1.3125 = 1 + 0.3125

0.3125 x 8 = 2.5 = 2 + 0.5

0.5 x 8 = 4.0 = 4 + 0

Thus: 0.1640625₁₀ = 0.124₈

These two methods can be combined to handle decimal numbers with both integer and fractional parts, using the first on the integer part and the second on the fractional part.

Octal to Decimal conversion

To convert a number k to decimal, use the formula that defines its base-8 representation:

$k = \sum_{i=0}^n \left( a_i\times 8^i \right).$

In this formula, a_i is an individual octal digit being converted, where i is the number of the digit (counting from 0 for the right-most digit).

Example: Convert 764₈ to decimal:

764₈ = 7 x 8² + 6 x 8¹ + 4 x 8° = 448 + 48 + 4 = 500₁₀

For double-digit octal numbers this method amounts to multiplying the lead digit by 8 and adding the second digit to get the total.

Example: 65₈ = 6x8 + 5 = 53₁₀

Octal to Binary Conversion

To convert octal to binary, replace each octal digit by its binary representation.

Example: Convert 51₈ to binary:

5₈ = 101₂

1₈ = 001₂

Thus: 51₈ = 101 001₂

Binary to Octal conversion

The process is the reverse of the previous algorithm. The binary digits are grouped by threes, starting from the decimal point and proceeding to the left and to the right. Add leading 0s (or trailing zeros to the right of decimal point) to fill out the last group of three if necessary. Then replace each trio with the equivalent octal digit.

For instance, convert binary 1010111100 to octal:

001	010	111	100
1	2	7	4

Thus 1010111100₂ = 1274₈

Convert binary 11100.01001 to octal:

011	100	.	010	010
3	4	.	2	2

Thus 11100.01001₂ = 34.22₈

Octal to Hexadecimal conversion

The conversion is made in two steps using binary as an intermediate base. Octal is converted to binary and then binary to hexadecimal, grouping digits by fours, which correspond each to a hexadecimal digit.

For instance, convert octal 1057 to hexadecimal:

To binary:

1	0	5	7
001	000	101	111

then to hexadecimal:

0010	0010	1111
2	2	F

Thus 1057₈ = 22F₁₆

Hexadecimal to Octal conversion

Reverse the previous algorithm.

References

↑ Avelino, Heriberto (2006). "The typology of Pame number systems and the limits of Mesoamerica as a linguistic area". Linguistic Typology 10: 41–60. doi:10.1515/LINGTY.2006.002. http://linguistics.berkeley.edu/~avelino/Avelino_2006.pdf
↑ Marcia Ascher. "Ethnomathematics: A Multicultural View of Mathematical Ideas". The College Mathematics Journal. http://links.jstor.org/sici?sici=0746-8342%28199209%2923%3A4%3C353%3AEAMVOM%3E2.0.CO%3B2-%23&size=LARGE. Retrieved 2007-04-13.
↑ Donald Knuth, The Art of Computer Programming
↑ ECMAScript 5th Edition: http://www.ecma-international.org/publications/files/drafts/tc39-2009-025.pdf
↑ Perl 6: http://svn.pugscode.org/pugs/docs/Perl6/Spec/S02-bits.pod
↑ Python 3: http://docs.python.org/3.1/reference/lexical_analysis.html#literals

External links

Online Converter for Decimal/Octal Numerals (JavaScript, GPL)
Octomatics is a numeral system enabling simple visual calculation in octal.