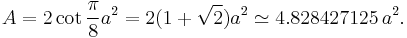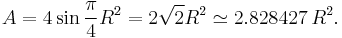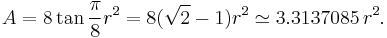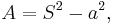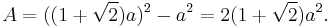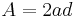Octagon
| Regular octagon | |
|---|---|
 A regular octagon |
|
| Edges and vertices | 8 |
| Schläfli symbols | {8} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D8) |
| Area (with a=edge length) |
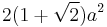 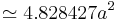 |
| Internal angle (degrees) |
135° |
| Properties | convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, an octagon is a polygon that has eight sides. A regular octagon is represented by the Schläfli symbol {8}.
Contents |
Regular octagons

A regular octagon is a closed figure with sides of the same length and internal angles of the same size. It has eight lines of reflective symmetry and rotational symmetry of order 8. The internal angle at each vertex of a regular octagon is 135° and the sum of all the internal angles is 1080° (as for any octagon). The area of a regular octagon of side length a is given by
In terms of  (circumradius), the area is
(circumradius), the area is
In terms of  (inradius), the area is
(inradius), the area is
These last two coefficients bracket the value of pi, the area of the unit circle.
The area can also be derived as follows:
where S is the span of the octagon, or the second shortest diagonal; and a is the length of one of the sides, or bases. This is easily proven if one takes an octagon, draws a square around the outside (making sure that four of the eight sides touch the four sides of the square) and then taking the corner triangles (these are 45-45-90 triangles) and placing them with right angles pointed inward, forming a square. The edges of this square are each the length of the base.
Given the span  , the length of a side
, the length of a side 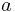 is:
is:
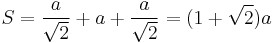
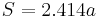 (approximately)
(approximately)
The area is then as above:
Another simple formula for the area is
where d is the distance between parallel sides (the same as span S in the diagram).
Standard coordinates
The coordinates for the vertices of a regular octagon centered at the origin and with side length 2 are:
- (±1, ±(1+√2))
- (±(1+√2), ±1).
Uses of octagons
 In many parts of the world, stop signs are in the shape of a regular octagon. |
 Umbrellas often have an octagonal outline. |
 The famous Bukhara rug design incorporates an octagonal "elephant's foot" motif. |
 The street & block layout of Barcelona's Eixample district is based on non-regular octagons |
 The famous Vichy Pastilles, octagon-shaped candies. |
Derived figures
 An eight-sided star, called an octagram, with Schläfli symbol {8/3} is contained with a regular octagon. |
 The vertex figure of the uniform polyhedron, great dirhombicosidodecahedron is contained within an irregular 8-sided star polygon, with four edges going through its center. |
 An octagonal prism contains two octagons. |
 The truncated square tiling has 2 octagons around every vertex. |
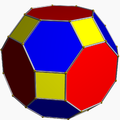 The truncated cuboctahedron contains 6 octagons. |
 An octagonal antiprism contains two octagons. |
Petrie polygons
The octagon is the Petrie polygon for eight higher dimensional polytopes, shown in these skew orthogonal projections:
| 4D | 5D | |||
|---|---|---|---|---|
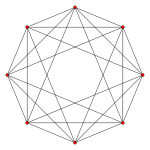 16-cell |
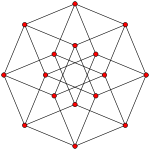 Tesseract |
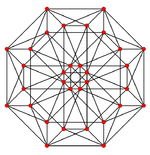 Rectified tesseract |
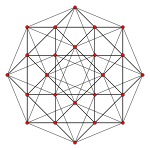 24-cell (Rectified 16-cell) |
 Demipenteract |
| 7D | 5D | |||
 7-simplex |
 Rectified 7-simplex |
 Birectified 7-simplex |
 Trirectified 7-simplex |
 Rectified demipenteract |
Construction
A regular octagon is constructible using compass and straightedge:
See also
- Octagram
- Octagonal number
- Octagon house
- Bumper pool
- Octa Star
External links
- Octagon Calculator
- Definition and properties of an octagon With interactive animation
- Weisstein, Eric W., "Octagon" from MathWorld.
|
|||||||||||||||||