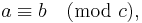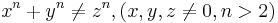Number theory

Number theory is the branch of pure mathematics concerned with the properties of numbers in general, and integers in particular, as well as the wider classes of problems that arise from their study.

Number theory may be subdivided into several fields, according to the methods used and the type of questions investigated. (See the list of number theory topics.)

The terms "arithmetic" or "the higher arithmetic" as nouns are also used to refer to elementary number theory. These are somewhat older terms, which are no longer as popular as they once were. However the word "arithmetic" is popularly used as an adjective rather than the more cumbersome phrase "number-theoretic", and also "arithmetic of" rather than "number theory of", e.g. arithmetic geometry, arithmetic functions, arithmetic of elliptic curves.

When arranging the natural numbers in a spiral and emphasizing the prime numbers, an intriguing and not fully explained pattern is observed, called the Ulam spiral.

Fields

Elementary number theory

In elementary number theory, integers are studied without use of techniques from other mathematical fields. Questions of divisibility, use of the Euclidean algorithm to compute greatest common divisors, integer factorizations into prime numbers, investigation of perfect numbers and congruences belong here. Several important discoveries of this field are Fermat's little theorem, Euler's theorem, the Chinese remainder theorem and the law of quadratic reciprocity. The properties of multiplicative functions such as the Möbius function and Euler's φ function, integer sequences, factorials, and Fibonacci numbers all also fall into this area.

Many questions in number theory can be stated in elementary number theoretic terms, but they may require very deep consideration and new approaches outside the realm of elementary number theory to solve. Examples include:

• Goldbach's conjecture concerning the expression of even numbers as sums of two primes.
• Mihăilescu's theorem (formerly Catalan's conjecture) regarding successive integer powers.
• The twin prime conjecture about the infinitude of prime pairs.
• The Collatz conjecture concerning a simple iteration.
• Fermat's Last Theorem (stated in 1637, but not proven until 1994) concerning the impossibility of finding nonzero integers x, y, z such that 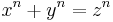for some integer n greater than 2.

The theory of Diophantine equations has even been shown to be undecidable (see Hilbert's tenth problem).

Analytic number theory

Analytic number theory employs the machinery of calculus and complex analysis to tackle questions about integers. The prime number theorem (PNT) and the related Riemann hypothesis are examples. Waring's problem (representing a given integer as a sum of squares, cubes etc.), the twin prime conjecture (finding infinitely many prime pairs with difference 2) and Goldbach's conjecture (writing even integers as sums of two primes) are being attacked with analytical methods as well. Proofs of the transcendence of mathematical constants, such as π or e, are also classified as analytical number theory. While statements about transcendental numbers may seem to be removed from the study of integers, they really study the possible values of polynomials with integer coefficients evaluated at, say, e; they are also closely linked to the field of Diophantine approximation, where one investigates "how well" a given real number may be approximated by a rational one.

Algebraic number theory

In algebraic number theory, the concept of a number is expanded to the algebraic numbers which are roots of polynomials with rational coefficients. These domains contain elements analogous to the integers, the so-called algebraic integers. In this setting, the familiar features of the integers (e.g. unique factorization) need not hold. The virtue of the machinery employed—Galois theory, group cohomology, class field theory, group representations and L-functions—is that it allows one to recover that order partly for this new class of numbers.

Many number theoretic questions are best attacked by studying them modulo p for all primes p (see finite fields). This leads to the construction of the p-adic numbers; this field of study is called local analysis and it arises from algebraic number theory.

Geometry of numbers

The geometry of numbers incorporates some basic geometric concepts, such as lattices, into number-theoretic questions. It starts with Minkowski's theorem about lattice points in convex sets, and leads to basic proofs of the finiteness of the class number and Dirichlet's unit theorem, two fundamental theorems in algebraic number theory.

Combinatorial number theory

Combinatorial number theory deals with number theoretic problems which involve combinatorial ideas in their formulations or solutions. Paul Erdős is the main founder of this branch of number theory. Typical topics include partitions, covering system, zero-sum problems, various restricted sumsets, and arithmetic progressions in a set of integers. Algebraic or analytic methods are powerful in this field. See also arithmetic combinatorics.

Computational number theory

Computational number theory studies algorithms relevant in number theory. Fast algorithms for prime testing and integer factorization have important applications in cryptography.

Arithmetic algebraic geometry

See arithmetic geometry.

Arithmetic topology

Arithmetic topology developed from a series of analogies between number fields and 3-manifolds; primes and knots pointed out by Barry Mazur and by Yuri Manin in the 1960s.

Arithmetic dynamics

Arithmetic dynamics is a field that emerged in the 1990s that amalgamates two areas of mathematics, dynamical systems and number theory. Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, p-adic, and/or algebraic points under repeated application of a polynomial or rational function.

Modular forms

Modular forms are (complex) analytic functions on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology and string theory.

History

Greek number theory

Number theory was a favorite study among the Greek mathematicians of the late Hellenistic period (3rd century AD) in Alexandria, Egypt, who were aware of the Diophantine equation concept in numerous special cases. The first Greek mathematician to study these equations was Diophantus.

Diophantus also looked for a method of finding integer solutions to linear indeterminate equations, equations that lack sufficient information to produce a single discrete set of answers. The equation 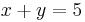is such an equation. Diophantus discovered that many indeterminate equations can be reduced to a form where a certain category of answers is known even though a specific answer is not.

Classical Indian number theory

Diophantine equations were extensively studied by mathematicians in medieval India, who were the first to systematically investigate methods for the determination of integral solutions of Diophantine equations. Aryabhata (499) gave the first explicit description of the general integral solution of the linear Diophantine equation 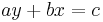, which occurs in his text Aryabhatiya. This kuttaka algorithm is considered to be one of the most significant contributions of Aryabhata in pure mathematics, which found solutions to Diophantine equations by means of continued fractions. The technique was applied by Aryabhata to give integral solutions of simultaneous linear Diophantine equations, a problem with important applications in astronomy. He also found the general solution to the indeterminate linear equation using this method.

Brahmagupta in 628 handled more difficult Diophantine equations. He used the chakravala method to solve quadratic Diophantine equations, including forms of Pell's equation, such as 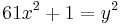. His Brahma Sphuta Siddhanta was translated into Arabic in 773 and was subsequently translated into Latin in 1126. The equation 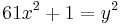was later posed as a problem in 1657 by the French mathematician Pierre de Fermat. The general solution to this particular form of Pell's equation was found over 70 years later by Leonhard Euler, while the general solution to Pell's equation was found over 100 years later by Joseph Louis Lagrange in 1767. Meanwhile, many centuries ago, the general solution to Pell's equation was recorded by Bhaskara II in 1150, using a modified version of Brahmagupta's chakravala method, which he also used to find the general solution to other indeterminate quadratic equations and quadratic Diophantine equations. Bhaskara's chakravala method for finding the general solution to Pell's equation was much simpler than the method used by Lagrange over 600 years later. Bhaskara also found solutions to other indeterminate quadratic, cubic, quartic, and higher-order polynomial equations. Narayana Pandit further improved on the chakravala method and found more general solutions to other indeterminate quadratic and higher-order polynomial equations.

Islamic number theory

From the 9th century, Islamic mathematics had a keen interest in number theory. The first of these mathematicians was Thabit ibn Qurra, who discovered an algorithm which allowed pairs of amicable numbers to be found, that is two numbers such that each is the sum of the proper divisors of the other. In the 10th century, Ibn Tahir al-Baghdadi looked at a slight variant of Thabit ibn Qurra's method.

In the 10th century, al-Haitham seems to have been the first to attempt to classify all even perfect numbers (numbers equal to the sum of their proper divisors) as those of the form 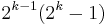where 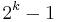is prime. Al-Haytham is also the first person to state Wilson's theorem, namely that if p is prime then 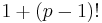is divisible by . It is unclear whether he knew how to prove this result. It is called Wilson's theorem because of a comment made by Edward Waring in 1770 that John Wilson had noticed the result. There is no evidence that Wilson knew how to prove it and most certainly Waring did not. Lagrange gave the first proof in 1771.

Amicable numbers played a large role in Islamic mathematics. In the 13th century, Persian mathematician Al-Farisi gave a new proof of Thabit ibn Qurra's theorem, introducing important new ideas concerning factorisation and combinatorial methods. He also gave the pair of amicable numbers 17296, 18416 which have been attributed to Euler, but we know that these were known earlier than al-Farisi, perhaps even by Thabit ibn Qurra himself. In the 17th century, Muhammad Baqir Yazdi gave the pair of amicable numbers 9,363,584 and 9,437,056 still many years before Euler's contribution.

Early European number theory

In the 13th century, Leonardo de Pisa (better known as Fibonacci), wrote one of his greatest works, the Liber Quadratorum. In this work he deals with Pythagorean triple. He noted that square numbers can be constructed as sums of odd numbers. He defined the concept of a congruum, a number of the form ab(a + b)(a - b), if a + b is even, and 4 times this if a + b is odd. Fibonacci proved that a congruum must be divisible by 24 and he also showed that for x, c such that x2 + c and x2 - c are both squares, then c is a congruum. He also proved that a square cannot be a congruum.^[1] His contribution to number theory were so great that it has been said that "the Liber quadratorum alone ranks Fibonacci as the major contributor to number theory between Diophantus and the 17th-century French mathematician Pierre de Fermat".^[2]

Further advances were done in the 16th and 17th centuries, with Vieta, Bachet de Meziriac, and especially Fermat, whose infinite descent method was the first general proof of diophantine questions. Fermat's Last Theorem was posed as a problem in 1637, a proof of which wasn't found until 1994. Fermat also posed the equation 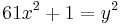as a problem in 1657.

In the eighteenth century, Euler and Lagrange made important contributions to number theory. Euler did some work on analytic number theory, and found a general solution to the equation 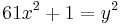. Lagrange found a solution to the more general Pell's equation. Euler and Lagrange solved these Pell equations by means of continued fractions, though this was more difficult than the Indian chakravala method.

Beginnings of modern number theory

Around the beginning of the nineteenth century books of Legendre (1798), and Gauss put together the first systematic theories in Europe. Gauss's Disquisitiones Arithmeticae (1801) may be said to begin the modern theory of numbers.

The formulation of the theory of congruences starts with Gauss's Disquisitiones. He introduced the notation

and explored most of the field. Chebyshev published in 1847 a work in Russian on the subject, and in France Serret popularised it.

Besides summarizing previous work, Legendre stated the law of quadratic reciprocity. This law, discovered by induction and enunciated by Euler, was first proved by Legendre in his Théorie des Nombres (1798) for special cases. Independently of Euler and Legendre, Gauss discovered the law about 1795, and was the first to give a general proof. The following have also contributed to the subject: Cauchy; Dirichlet whose Vorlesungen über Zahlentheorie is a classic; Jacobi, who introduced the Jacobi symbol; Liouville, Zeller, Eisenstein, Kummer, and Kronecker. The theory extends to include cubic and quartic reciprocity, (Gauss, Jacobi who first proved the law of cubic reciprocity, and Kummer).

To Gauss is also due the representation of numbers by binary quadratic forms.

Prime number theory

A recurring and productive theme in number theory is the study of the distribution of prime numbers. Carl Friedrich Gauss conjectured an asymptotic rule for such behaviour (the prime number theorem) as a teenager.

Dirichlet (1837) proved that every eligible arithmetic progression contains infinitely many prime numbers. Chebyshev (1850) gave useful bounds for the number of primes between two given limits. Riemann introduced complex analysis into the theory of the Riemann zeta function. This led to a relation between the zeros of the zeta function and the distribution of primes, eventually leading to a proof of prime number theorem independently by Hadamard and de la Vallée Poussin in 1896. However, an elementary proof was given later by Paul Erdős and Atle Selberg in 1949. Here elementary means that it does not use techniques of complex analysis; however, the proof is still very ingenious and difficult. The Riemann hypothesis, which would give much more accurate information, is still an open question.

Nineteenth-century developments

Cauchy, Poinsot (1845), and notably Hermite have added to the subject. In the theory of ternary forms, Eisenstein has been a leader, and to him and H. J. S. Smith is also due a noteworthy advance in the theory of forms in general. Smith gave a complete classification of ternary quadratic forms, and extended Gauss's researches concerning real quadratic forms to complex forms. The investigations concerning the representation of numbers by the sum of 4, 5, 6, 7, 8 squares were advanced by Eisenstein and the theory was completed by Smith.

Dirichlet was the first to lecture upon the subject in a German university. Among his contributions is the proof of Fermat's Last Theorem:

for the cases n = 5 and n = 14 (Euler and Legendre had already proved the cases n = 3 and n = 4 and therefore by implication, all multiples of 3 and 4). Among the later French writers are Borel; Poincaré, whose memoirs are numerous and valuable; Tannery, and Stieltjes. Among the leading contributors in Germany were Leopold Kronecker, Ernst Kummer, Ernst Christian Julius Schering, Paul Bachmann, and Dedekind. In Austria Stolz's Vorlesungen über allgemeine Arithmetik (1885–86), and in England Mathews' Theory of Numbers (Part I, 1892) were scholarly general works. Genocchi, Sylvester, and J. W. L. Glaisher have also added to the theory.

Late nineteenth- and early twentieth-century developments

It was the time of major advancements in number theory due to the work of Axel Thue on Diophantine equations, of David Hilbert in algebraic number theory and the solution of Waring's problem, and to the creation of geometric number theory by Hermann Minkowski, but also thanks to Adolf Hurwitz, Georgy F. Voronoy, Waclaw Sierpinski, Derrick Norman Lehmer and several others.

Twentieth-century developments

Major figures in twentieth-century number theory include Hermann Weyl, Nikolai Chebotaryov, Emil Artin, Erich Hecke, Helmut Hasse, Alexander Gelfond, Yuri Linnik, Paul Erdős, Gerd Faltings, G. H. Hardy, Edmund Landau, Louis Mordell, John Edensor Littlewood, Ivan Niven, Srinivasa Ramanujan, André Weil, Ivan Vinogradov, Atle Selberg, Carl Ludwig Siegel, Igor Shafarevich, John Tate, Robert Langlands, Goro Shimura, Kenkichi Iwasawa, Jean-Pierre Serre, Pierre Deligne, Enrico Bombieri, Alan Baker, Peter Swinnerton-Dyer, Bryan Birch, Vladimir Drinfeld, Laurent Lafforgue, Andrew Wiles, and Richard Taylor.

Milestones in twentieth-century number theory include:

• The development of class field theory, its completion—Teiji Takagi, Emil Artin, Philipp Furtwängler in the 1920s—and its extensions and reformulations—Helmut Hasse, Claude Chevalley in the 1930s.
• The Weil conjectures introduced by André Weil in the 1940s, and their proof in the work of Bernard Dwork, Alexander Grothendieck, Pierre Deligne, and others.
• Barban's theorem in 1961 and its 1965 refinement, the Bombieri–Vinogradov theorem.
• The creation of the Langlands program by Robert Langlands in the late 1960s, and subsequent progress by many mathematicians.
• Chen's theorem stated in 1966 and proved in 1973
• The proof of Fermat's Last Theorem by Andrew Wiles, and the proof of the full Taniyama–Shimura conjecture in 1999 by Christophe Breuil, Brian Conrad, Fred Diamond, and Richard Taylor.

Twenty-first-century developments

• The Green–Tao theorem, proved in 2004, which states that no matter how large n is, there is an arithmetic progression of n prime numbers.

Applied number theory

The book "Number theory for computing"^[3] says that number theory has been applied to: "physics, chemistry, biology, computing, engineering, coding and cryptography, random number generation, acoustics, communications, graphic design and even music and business." It also says that Shiing-Shen Chern "considers number theory as a branch of applied mathematics because of its strong applicability in other fields." For example, problems in the analysis of nonlinear resonances in fluid mechanics can be formulated in the form of Diophantine equations and solved by the method of q-class decomposition.^[4]

Public-key cryptography

Many public-key cryptography schemes use number theory e.g. RSA Cryptosystem, Elliptic curve cryptography.

Residue number system

A residue number system (RNS) represents a large integer using a set of smaller integers, so that computation may be performed more efficiently. It relies on the Chinese remainder theorem of modular arithmetic for its operation. RNS have applications in the field of digital computer arithmetic. By decomposing in this a large integer into a set of smaller integers, a large calculation can be performed as a series of smaller calculations that can be performed independently and in parallel. Because of this, it is particularly popular in hardware implementations.

Integer programming

The LLL algorithm is used in integer linear programming.

Quotations

• "Mathematics is the queen of the sciences and number theory is the queen of mathematics." — Gauss^[5]
• "God invented the integers; all else is the work of man." — Kronecker^[6]
• "Number is the within of all things." — Attributed to Pythagoras^[7]

Notes

References & further reading

• Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, MR0434929, ISBN 978-0-387-90163-3 
• Dedekind, Richard (1963). Essays on the Theory of Numbers. Cambridge University Press. ISBN 0-486-21010-3. 
• Davenport, Harold (1999). The Higher Arithmetic: An Introduction to the Theory of Numbers (7th ed.). Cambridge University Press. ISBN 0-521-63446-6. 
• Guy, Richard K. (1981). Unsolved Problems in Number Theory. Springer-Verlag. ISBN 0-387-90593-6. 
• Hardy, G. H. and Wright, E. M. (1980). An Introduction to the Theory of Numbers (5th ed.). Oxford University Press. ISBN 0-19-853171-0. 
• Niven, Ivan, Zuckerman, Herbert S. and Montgomery, Hugh L. (1991). An Introduction to the Theory of Numbers (5th ed.). Wiley Text Books. ISBN 0-471-62546-9. 
• Ore, Oystein (1948). Number Theory and Its History. Dover Publications, Inc.. ISBN 0-486-65620-9. 
• Smith, David. History of Modern Mathematics (1906) (adapted public domain text)
• Dutta, Amartya Kumar (2002). 'Diophantine equations: The Kuttaka', Resonance - Journal of Science Education.
• O'Connor, John J. and Robertson, Edmund F. (2004). 'Arabic/Islamic mathematics', MacTutor History of Mathematics archive.
• O'Connor, John J. and Robertson, Edmund F. (2004). 'Index of Ancient Indian mathematics', MacTutor History of Mathematics archive.
• O'Connor, John J. and Robertson, Edmund F. (2004). 'Numbers and Number Theory Index', MacTutor History of Mathematics archive.
• Kraeft, Uwe, (2000–2010). 'Studies in Number Theory', 22 vols., last vol. 'Additive Representations of Integers in Number Theory', Shaker Verlag, Aachen, ISBN 978-3-8322-8793-1.
• Important publications in number theory

External links

• Number Theory Web
• A Computational Introduction to Number Theory and Algebra by Victor Shoup