Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges. Typically, a graph is depicted in diagrammatic form as a set of dots for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
The edges may be directed (asymmetric) or undirected (symmetric). For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this is an undirected graph, because if person A shook hands with person B, then person B also shook hands with person A. On the other hand, if the vertices represent people at a party, and there is an edge from person A to person B when person A knows of person B, then this graph is directed, because knowing of someone is not necessarily a symmetric relation (that is, one person knowing of another person does not necessarily imply the reverse; for example, many fans may know of a celebrity, but the celebrity is unlikely to know of all their fans). This latter type of graph is called a directed graph and the edges are called directed edges or arcs; in contrast, a graph where the edges are not directed is called undirected.
Vertices are also called nodes or points, and edges are also called lines. Graphs are the basic subject studied by graph theory. The word "graph" was first used in this sense by James Joseph Sylvester in 1878.[1]
Contents |
Definitions
Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures.
Graph

In the most common sense of the term,[2] a graph is an ordered pair G = (V, E) comprising a set V of vertices or nodes together with a set E of edges or lines, which are 2-element subsets of V (i.e, an edge is related with two vertices, and the relation is represented as unordered pair of the vertices with respect to the particular edge). To avoid ambiguity, this type of graph may be described precisely as undirected and simple.
Other senses of graph stem from different conceptions of the edge set. In one more generalized notion,[3] E is a set together with a relation of incidence that associates with each edge two vertices. In another generalized notion, E is a multiset of unordered pairs of (not necessarily distinct) vertices. Many authors call this type of object a multigraph or pseudograph.
All of these variants and others are described more fully below.
The vertices belonging to an edge are called the ends, endpoints, or end vertices of the edge. A vertex may exist in a graph and not belong to an edge.
V and E are usually taken to be finite, and many of the well-known results are not true (or are rather different) for infinite graphs because many of the arguments fail in the infinite case. The order of a graph is 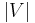 (the number of vertices). A graph's size is
(the number of vertices). A graph's size is 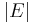 , the number of edges. The degree of a vertex is the number of edges that connect to it, where an edge that connects to the vertex at both ends (a loop) is counted twice.
, the number of edges. The degree of a vertex is the number of edges that connect to it, where an edge that connects to the vertex at both ends (a loop) is counted twice.
For an edge {u, v}, graph theorists usually use the somewhat shorter notation uv.
Adjacency relation
The edges E of an undirected graph G induce a symmetric binary relation ~ on V that is called the adjacency relation of G. Specifically, for each edge {u, v} the vertices u and v are said to be adjacent to one another, which is denoted u ~ v.
Types of graphs
Distinction in terms of the main definition
As stated above, in different contexts it may be useful to define the term graph with different degrees of generality. Whenever it is necessary to draw a strict distinction, the following terms are used. Most commonly, in modern texts in graph theory, unless stated otherwise, graph means "undirected simple finite graph" (see the definitions below).
Undirected graph
A graph in which edges have no orientation, i.e., they are not ordered pairs, but sets {u, v} (or 2-multisets) of vertices.
Directed graph
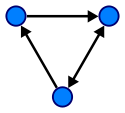
A directed graph or digraph is an ordered pair D = (V, A) with
- V a set whose elements are called vertices or nodes, and
- A a set of ordered pairs of vertices, called arcs, directed edges, or arrows.
An arc a = (x, y) is considered to be directed from x to y; y is called the head and x is called the tail of the arc; y is said to be a direct successor of x, and x is said to be a direct predecessor of y. If a path leads from x to y, then y is said to be a successor of x and reachable from x, and x is said to be a predecessor of y. The arc (y, x) is called the arc (x, y) inverted.
A directed graph D is called symmetric if, for every arc in D, the corresponding inverted arc also belongs to D. A symmetric loopless directed graph D = (V, A) is equivalent to a simple undirected graph G = (V, E), where the pairs of inverse arcs in A correspond 1-to-1 with the edges in E; thus the edges in G number |E| = |A|/2, or half the number of arcs in D.
A variation on this definition is the oriented graph, in which not more than one of (x, y) and (y, x) may be arcs.
Mixed graph
A mixed graph G is a graph in which some edges may be directed and some may be undirected. It is written as an ordered triple G = (V, E, A) with V, E, and A defined as above. Directed and undirected graphs are special cases.
Multigraph
A loop is an edge (directed or undirected) which starts and ends on the same vertex; these may be permitted or not permitted according to the application. In this context, an edge with two different ends is called a link.
The term "multigraph" is generally understood to mean that multiple edges (and sometimes loops) are allowed. Where graphs are defined so as to allow loops and multiple edges, a multigraph is often defined to mean a graph without loops,[4] however, where graphs are defined so as to disallow loops and multiple edges, the term is often defined to mean a "graph" which can have both multiple edges and loops,[5] although many use the term "pseudograph" for this meaning.[6]
Simple graph

As opposed to a multigraph, a simple graph is an undirected graph that has no loops and no more than one edge between any two different vertices. In a simple graph the edges of the graph form a set (rather than a multiset) and each edge is a pair of distinct vertices. In a simple graph with n vertices every vertex has a degree that is less than n (the converse, however, is not true - there exist non-simple graphs with n vertices in which every vertex has a degree smaller than n).
Weighted graph
A graph is a weighted graph if a number (weight) is assigned to each edge. Such weights might represent, for example, costs, lengths or capacities, etc. depending on the problem.
The weight of the graph is the sum of the weights given to all edges.
Half-edges, loose edges
In exceptional situations it is even necessary to have edges with only one end, called half-edges, or no ends (loose edges); see for example signed graphs and biased graphs.
Important graph classes
Regular graph
A regular graph is a graph where each vertex has the same number of neighbors, i.e., every vertex has the same degree or valency. A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.
Complete graph
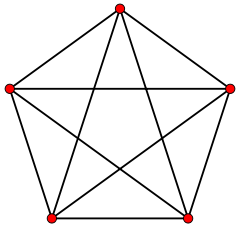
Complete graphs have the feature that each pair of vertices has an edge connecting them.
Finite and infinite graphs
A finite graph is a graph G = (V, E) such that V and E are finite sets. An infinite graph is one with an infinite set of vertices or edges or both.
Most commonly in graph theory it is implied that the graphs discussed are finite. If the graphs are infinite, that is usually specifically stated.
Graph classes in terms of connectivity
In an undirected graph G, two vertices u and v are called connected if G contains a path from u to v. Otherwise, they are called disconnected. A graph is called connected if every pair of distinct vertices in the graph is connected; otherwise, it is called disconnected.
A graph is called k-vertex-connected or k-edge-connected if removal some set of k or more vertices (respectively, edges) makes the graph disconnected. A k-vertex-connected graph is often called simply k-connected.
A directed graph is called weakly connected if replacing all of its directed edges with undirected edges produces a connected (undirected) graph. It is strongly connected or strong if it contains a directed path from u to v and a directed path from v to u for every pair of vertices u, v.
Properties of graphs
Two edges of a graph are called adjacent (sometimes coincident) if they share a common vertex. Two arrows of a directed graph are called consecutive if the head of the first one is at the nock (notch end) of the second one. Similarly, two vertices are called adjacent if they share a common edge (consecutive if they are at the notch and at the head of an arrow), in which case the common edge is said to join the two vertices. An edge and a vertex on that edge are called incident.
The graph with only one vertex and no edges is called the trivial graph. A graph with only vertices and no edges is known as an edgeless graph. The graph with no vertices and no edges is sometimes called the null graph or empty graph, but the terminology is not consistent and not all mathematicians allow this object.
In a weighted graph or digraph, each edge is associated with some value, variously called its cost, weight, length or other term depending on the application; such graphs arise in many contexts, for example in optimal routing problems such as the traveling salesman problem.
Normally, the vertices of a graph, by their nature as elements of a set, are distinguishable. This kind of graph may be called vertex-labeled. However, for many questions it is better to treat vertices as indistinguishable; then the graph may be called unlabeled. (Of course, the vertices may be still distinguishable by the properties of the graph itself, e.g., by the numbers of incident edges). The same remarks apply to edges, so that graphs which have labeled edges are called edge-labeled graphs. Graphs with labels attached to edges or vertices are more generally designated as labeled. Consequently, graphs in which vertices are indistinguishable and edges are indistinguishable are called unlabeled. (Note that in the literature the term labeled may apply to other kinds of labeling, besides that which serves only to distinguish different vertices or edges.)
Examples

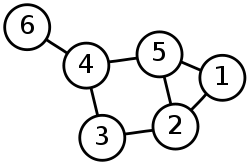
The picture is a graphic representation of the following graph
- V = {1, 2, 3, 4, 5, 6}
- E = {{1, 2}, {1, 5}, {2, 3}, {2, 5}, {3, 4}, {4, 5}, {4, 6}}.
The fact that vertex 1 is adjacent to vertex 2 is sometimes denoted by 1 ~ 2.
- In category theory a small category can be considered a directed multigraph with the objects as vertices and the morphisms as directed edges. The functors between categories induce then some, but not necessarily all, of the digraph morphisms.
- In computer science directed graphs are used to represent knowledge (e.g., Conceptual graph), finite state machines and many other discrete structures.
- A binary relation R on a set X is a directed graph. Two elements x, y of X are connected by an arrow iff xRy.
Important graphs
Basic examples are:
- In a complete graph each pair of vertices is joined by an edge, that is, the graph contains all possible edges.
- In a bipartite graph, the vertices can be divided into two sets, W and X, so that every edge has one vertex in each of the two sets.
- In a complete bipartite graph, the vertex set is the union of two disjoint subsets, W and X, so that every vertex in W is adjacent to every vertex in X but there are no edges within W or X.
- In a linear graph or path graph of length n, the vertices can be listed in order, v0, v1, ..., vn, so that the edges are vi−1vi for each i = 1, 2, ..., n. If a linear graph occurs as a subgraph of another graph, it is a path in that graph.
- In a cycle graph of length n vertices can be named v1, ..., vn with n at least 3, so that the edges are vi−1vi for each i = 2,...,n and vnv1. Cycle graphs can be characterized as connected graphs with degree 2 at every vertex. If a cycle graph occurs as a subgraph of another graph, it defines a cycle or circuit in that graph.
- A planar graph can be drawn in a plane with no crossing edges (i.e., embedded in a plane).
- A tree is a connected graph with no cycles.
- A forest is a graph with no cycles (i.e. one or more trees).
More advanced kinds of graphs are:
- The Petersen graph and its generalizations
- Perfect graphs
- Cographs
- Other graphs with large automorphism groups: vertex-transitive, arc-transitive, and distance-transitive graphs.
- Strongly regular graphs and their generalization distance-regular graphs.
Operations on graphs
There are several operations that produce new graphs from old ones, which might be classified into the following categories:
- Elementary operations, sometimes called "editing operations" on graphs, which create a new graph from the original one by a simple, local change, such as addition or deletion of a vertex or an edge, merging and splitting of vertices, etc.
- Graph rewrite operations replacing the occurrence of some pattern graph within the host graph by an instance of the corresponding replacement graph.
- Unary operations, which create a significantly new graph from the old one. Examples:
- Line graph
- Dual graph
- Complement graph
- Binary operations, which create new graph from two initial graphs. Examples:
- Disjoint union of graphs
- Cartesian product of graphs
- Tensor product of graphs
- Strong product of graphs
- Lexicographic product of graphs
Generalizations
In a hypergraph, an edge can join more than two vertices.
An undirected graph can be seen as a simplicial complex consisting of 1-simplices (the edges) and 0-simplices (the vertices). As such, complexes are generalizations of graphs since they allow for higher-dimensional simplices.
Every graph gives rise to a matroid.
In model theory, a graph is just a structure. But in that case, there is no limitation on the number of edges: it can be any cardinal number, see continuous graph.
In computational biology, power graph analysis introduces power graphs as an alternative representation of undirected graphs.
See also
- Dual graph
- Glossary of graph theory
- Graph (data structure)
- Graph database
- Graph drawing
- Graph theory publications
- List of graph theory topics
- Network theory
- Conceptual graph
- Horizontal constraint graph
- Causal dynamical triangulation
- Sage Math (software)
- NetworkX (software)
Notes
- ↑ Gross, Jonathan L.; Yellen, Jay (2004). Handbook of graph theory. CRC Press. p. 35. ISBN 9781584880905. http://books.google.com/?id=mKkIGIea_BkC
- ↑ See, for instance, Iyanaga and Kawada, 69 J, p. 234 or Biggs, p. 4.
- ↑ See, for instance, Graham et al., p. 5.
- ↑ For example, see Balakrishnan, p. 1, Gross (2003), p. 4, and Zwillinger, p. 220.
- ↑ For example, see. Bollobas, p. 7 and Diestel, p. 25.
- ↑ Gross (1998), p. 3, Gross (2003), p. 205, Harary, p.10, and Zwillinger, p. 220.
References
- Balakrishnan, V. K. (1997-02-01). Graph Theory (1st ed.). McGraw-Hill. ISBN 0-07-005489-4.
- Berge, Claude (1958) (in French). Théorie des graphes et ses applications. Dunod, Paris: Collection Universitaire de Mathématiques, II. pp. viii+277. Translation: (in English). Dover, New York: Wiley. 2001 [1962].
- Biggs, Norman (1993). Algebraic Graph Theory (2nd ed.). Cambridge University Press. ISBN 0-521-45897-8.
- Bollobas, Bela (2002-08-12). Modern Graph Theory (1st ed.). Springer. ISBN 0-387-98488-7.
- Bang-Jensen, J.; Gutin, G. (2000). Digraphs: Theory, Algorithms and Applications. Springer. http://www.cs.rhul.ac.uk/books/dbook/.
- Diestel, Reinhard (2005). Graph Theory (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-3-540-26183-4. http://diestel-graph-theory.com/GrTh.html.
- Graham, R.L., Grötschel, M., and Lovász, L, ed (1995). Handbook of Combinatorics. MIT Press. ISBN 0-262-07169-X.
- Gross, Jonathan L.; Yellen, Jay (1998-12-30). Graph Theory and Its Applications. CRC Press. ISBN 0-8493-3982-0.
- Gross, Jonathan L., & Yellen, Jay, ed (2003-12-29). Handbook of Graph Theory. CRC. ISBN 1-58488-090-2.
- Harary, Frank (January 1995). Graph Theory. Addison Wesley Publishing Company. ISBN 0-201-41033-8.
- Iyanaga, Shôkichi; Kawada, Yukiyosi (1977). Encyclopedic Dictionary of Mathematics. MIT Press. ISBN 0-262-09016-3.
- Zwillinger, Daniel (2002-11-27). CRC Standard Mathematical Tables and Formulae (31st ed.). Chapman & Hall/CRC. ISBN 1-58488-291-3.
External links
- Graph theory tutorial
- Image gallery : Some real-life graphs
- A searchable database of small connected graphs
- VisualComplexity.com — A visual exploration on mapping complex networks
- Weisstein, Eric W., "Graph" from MathWorld.
- Intelligent Graph Visualizer — IGV create and edit graph, automatically places graph, search shortest path (+coloring vertices), center, degree, eccentricity, etc.