Tuple
In mathematics and computer science a tuple is an ordered list of elements. In set theory, an (ordered) n-tuple is a sequence (or ordered list) of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair. Tuples are usually written by listing the elements within parentheses '( )' and separated by commas; for example, (2, 7, 4, 1, 7) denotes a 5-tuple. Sometimes other delimiters are used, such as brackets '[ ]' or angle brackets '⟨ ⟩'. Braces '{ }' are almost never used for tuples, as they are the standard notation for sets.
Tuples are often used to describe other mathematical objects. In algebra, for example, a ring is commonly defined as a 3-tuple (E,+,×), where E is some set, and '+', and '×' are functions from the Cartesian product E×E to E with specific properties. In computer science, tuples are directly implemented as product types in most functional programming languages. More commonly, they are implemented as record types, where the components are labeled instead of being identified by position alone. This approach is also used in relational algebra.
Contents |
Origin of name
The term originated as an abstraction of the sequence: single, double, triple, quadruple, quintuple, sextuple, septuple, octuple, ..., n-tuple, ... The unique 0-tuple is called the null tuple. A 1-tuple is called a singleton, a 2-tuple is called a pair and a 3-tuple is a triple or triplet. The n can be any nonnegative integer. For example, a complex number can be represented as a 2-tuple, a quaternion can be represented as a 4-tuple, an octonion can be represented as an octuple, (many mathematicians write the abbreviation "8-tuple") and a sedenion can be represented as a 16-tuple.
Although these uses treat -tuple as the suffix, the original suffix was -ple as in "decuple", ten-fold. This originates from a medieval Latin suffix -plus, "more", related to Greek -πλοῦς, which replaced the classical and late antique -plex "folded".[1]
Formal definitions
Characteristic properties
The main properties that distinguish a tuple from, for example, a set are that
- it can contain an object more than once;
- the objects appear in a certain order;
- it has finite size.
Note that (1) distinguishes it from an ordered set and that (2) distinguishes it from a multiset. This is often formalized by giving the following rule for the identity of two n-tuples:
- (a1, a2, …,an) = (b1, b2, …, bn) if and only if a1 = b1, a2 = b2, …, and an = bn.
Tuples as functions
An n-tuple can also be regarded as a function whose domain is the natural numbers { 1, 2, …, n } (or { 0, 1, …, n-1 }); that is, a set of index-element pairs:
- (a1, a2, …,an) ≡ { (1, a1), (2, a2), … (n, an) }
or
- (a0, a1, …,an−1) ≡ { (0, a0), (1, a1), … (n−1, an−1) }.
Tuples as nested ordered pairs
Another way of formalizing tuples is as nested ordered pairs. Namely,
- the 0-tuple (i.e. the empty tuple) is represented by the empty set Ø;
- an n-tuple, with n > 0, can be defined as an ordered pair of its first entry and an (n−1)-tuple containing the remaining entries:
- (a1, a2, …, an) = ( a1, (a2, …, an-1, an)).
Thus, for example, the tuple (3, 5, 3) would be the same as (3,(5,(3,Ø))).
This definition mirrors the most common representation of tuples as linked lists — as used, for example, in standard implementations of the Lisp programming language.
A variant of this definition starts "peeling off" elements from the other end:
- the 0-tuple is the empty set Ø;
- for n > 0,
- (a1, a2, …, an) = ((a1, a2, …, an-1), an).
Thus, for example, the tuple (3, 5, 3) would be the same as (((Ø,3),5),3).
Tuples as nested sets
Using Kuratowski's representation for an ordered pair, the second definition above can be reformulated in terms of pure set theory as:
- the 0-tuple (i.e. the empty tuple) is represented by the empty set Ø;
- if x is an n-tuple, and a is any element, then { {x}, {x,a} } is an (n + 1)-tuple.
In this formulation, the tuple (3, 5, 3) would be
- { { (3, 5) }, { (3, 5), 3 } } =
- { { { { (3) }, { (3), 5 } } }, { { { (3) }, { (3), 5 } }, 3 } } =
- { { { { { { Ø }, { Ø, 3 } } }, { { { Ø }, { Ø, 3 } }, 5 } } }, { { { { { Ø }, { Ø, 3 } } }, { { { Ø }, { Ø, 3 } }, 5 } }, 3 } }
Relational model
In database theory, the relational model uses a definition similar with tuples as functions above, but each tuple element is identified by a distinct name, called an attribute, instead of a number. A tuple in the relational model is formally defined as a finite function that maps attributes to values. Its purpose is the same as in mathematics, that is, to indicate that an object consists of certain components, but the components are identified by name instead of position, which leads to a more user-friendly and practical notation,[2] for example:
- ( player : "Harry", score : 25 )
In this notation, attribute–value pairs may appear in any order. The distinction between tuples in the relational model and those in set theory is only superficial. Imposing an arbitrary total order on the attributes, e.g. player ≤ score in the above example, and then ignoring the attribute names yields a 2-tuple. Conversely, a 2-tuple may be interpreted as relational model tuple over the attributes {1, 2}.[2]
In the relational model, a relation is a (possibly empty) finite set of tuples all having the same finite set of attributes, which is more formally called the sort of the relation, or just referred to as column names.[2] A tuple is usually implemented as a row in a database table, but see relational algebra for means of deriving tuples not physically represented in a table.
Type theory
In type theory, commonly used in programming languages, a tuple has a product type; this fixes not only the length, but also the underlying types of each component. Formally (x1, ...,xn) : T1×...×Tn, and the projections are term constructors π1(x) : T1, ..., πn(x) : Tn. The tuple with labeled elements used in the relational model (see section above) has a record type. Both of these types can be defined as simple extensions of simply typed lambda calculus.[3]
The notion of a tuple in type theory and that in set theory are related in the following way: If we consider the natural model of a type theory, and use the Scott brackets to indicate the semantic interpretation, then the model consists of some sets T1, ..., Tn (note: the use of italics here that distinguishes sets from types) such that 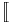 T1
T1![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) = T1, ...,
= T1, ..., 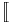 Tn
Tn![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) = Tn, and the interpretation of the basic terms is
= Tn, and the interpretation of the basic terms is 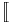 x1
x1![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png)

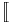 T1
T1![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) , ...,
, ..., 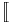 xn
xn![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png)

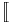 Tn
Tn![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) . The type theory tuple has the natural interpretation as a set theory n-tuple:
. The type theory tuple has the natural interpretation as a set theory n-tuple: 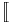 (x1, ...,xn)
(x1, ...,xn)![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) = (
= (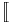 x1
x1![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) , ...,
, ...,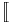 xn
xn![]\!]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71a302ebed4488ad0102291a8cf3ad13.png) ).[4] The unit type has as semantic interpretation the 0-tuple.
).[4] The unit type has as semantic interpretation the 0-tuple.
See also
- Arity
- Exponential object
- Formal language
- OLAP: Multidimensional Expressions
- Relation (mathematics)
- Tuplespace
References
- ↑ OED, s.v. "triple", "quadruple", "quintuple", "decuple"
- ↑ 2.0 2.1 2.2 Serge Abiteboul, Richard Hull, Victor Vianu, Foundations of databases, Addison-Wesley, 1995, ISBN 0201537710, p. 29–33
- ↑ Pierce, Benjamin (2002). Types and Programming Languages. MIT Press. pp. 126–132. ISBN 0-262-16209-1.
- ↑ Steve Awodey, From sets, to types, to categories, to sets, 2009, preprint
The set theory definitions herein are found in any textbook on the topic, e.g.
- Gaisi Takeuti, W. M. Zaring, Introduction to Axiomatic Set Theory, Springer GTM 1, 1971, ISBN 978-0-387-90024-7, p. 14
- Abraham Adolf Fraenkel, Yehoshua Bar-Hillel, Azriel Lévy, Foundations of set theory, Elsevier Studies in Logic Vol. 67, Edition 2, revised, 1973, ISBN 0720422701, p. 33
- Keith Devlin, The Joy of Sets. Springer Verlag, 2nd ed., 1993, ISBN 0-387-94094-4, pp. 7-8
- George J. Tourlakis, Lecture Notes in Logic and Set Theory. Volume 2: Set theory, Cambridge University Press, 2003, ISBN 978-0-521-75374-6, pp. 182-193