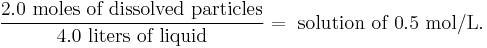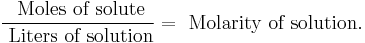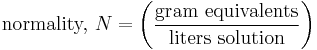Concentration

In chemistry, concentration is the measure of how much of a given substance there is mixed with another substance. This can apply to any sort of chemical mixture, but most frequently the concept is limited to homogeneous solutions, where it refers to the amount of solute in the solvent.

To concentrate a solution, one must add more solute (e.g. alcohol), or reduce the amount of solvent (e.g. water). By contrast, to dilute a solution, one must add more solvent, or reduce the amount of solute.

Unless two substances are fully miscible there exists a concentration at which no further solute will dissolve in a solution. At this point, the solution is said to be saturated. If additional solute is added to a saturated solution, it will not dissolve (except in certain circumstances, when supersaturation may occur). Instead, phase separation will occur, leading to either coexisting phases or a suspension. The point of saturation depends on many variables such as ambient temperature and the precise chemical nature of the solvent and solute.

Analytical concentration includes all the forms of that substance in the solution.

Qualitative description

These glasses containing red dye demonstrate qualitative changes in concentration. The solutions on the left are more dilute, compared to the more concentrated solutions on the right.

Often in informal, non-technical language, concentration is described in a qualitative way, through the use of adjectives such as "dilute" for solutions of relatively low concentration and of others like "concentrated" for solutions of relatively high concentration. Those terms relate the amount of a substance in a mixture to the observable intensity of effects or properties caused by that substance. For example, a practical rule is that the more concentrated a chromatic solution is, the more intensely colored it is (usually).

Quantitative notation

For scientific or technical applications, a qualitative account of concentration is almost never sufficient; therefore quantitative measures are needed to describe concentration. There are a number of different ways to quantitatively express concentration; the most common are listed below. They are based on mass, volume, or both. Depending on what they are based on it is not always trivial to convert one measure to the other, because knowledge of the density might be needed to do so. At times this information may not be available, particularly if the temperature varies.

Mass versus volume

Units of concentration — particularly the most popular one, molarity — require knowledge of a substance's volume, which unlike mass is variable depending on ambient temperature and pressure. In fact (partial) molar volume can even be a function of concentration itself. This is why volumes are not necessarily completely additive when two liquids are added and mixed. Volume-based measures for concentration are therefore not to be recommended for non-dilute solutions or problems where relatively large differences in temperature are encountered (e.g. for phase diagrams).

Unless otherwise stated, all the following measurements of volume are assumed to be at a standard state temperature and pressure (for example 0 degrees Celsius at 1 atmosphere or 101.325 kPa). The measurement of mass does not require such restrictions.

Mass can be determined at a precision of < 0.2 mg on a routine basis with an analytical balance and more precise instruments exist. Both solids and liquids are easily quantified by weighing.

The volume of a liquid is usually determined by calibrated glassware such as burrettes and volumetric flasks. For very small volumes precision syringes are available. The use of graduated beakers and cylinders is not recommended as their indication of volume is mostly for decorative rather than quantitative purposes. The volume of solids, particularly of powders, is often difficult to measure, which is why mass is the more usual measure. For gases the opposite is true: the volume of a gas can be measured in a gas burette, if care is taken to control the pressure, but the mass is not easy to measure due to buoyancy effects.

Molarity

See also: Molar concentration

Molarity (in units of mol/L, molar, or M) or molar concentration denotes the number of moles of a given substance per liter of solution. A capital letter M is used to abbreviate units of mol/L. For instance:

The actual formula for molarity is:

Such a solution may be described as "0.50 molar." It must be emphasized a 0.5 molar solution contains 0.5 moles of solute in 1.0 liter of solution. This is not equivalent to 1.0 liter of solvent. A 0.5 mol/L solution will contain either slightly more or slightly less than 1 liter of solvent because the process of dissolution causes volume of liquid to increase or decrease.

Following the SI system of units, the National Institute of Standards and Technology, the United States authority on measurement, considers the term molarity and the unit symbol M to be obsolete, and suggests instead the amount-of-substance concentration (c) with the units mol/m³ or other units used alongside the SI such as mol/L^[1]. This recommendation has not been universally implemented in academia or chemistry research yet.

Preparation of a solution of known molarity involves adding an accurately weighed amount of solute to a volumetric flask, adding some solvent to dissolve it, then adding more solvent to fill to the volume mark.

When discussing molarity of minute concentrations, such as in pharmacological research, molarity is expressed in units of millimolar (mmol/L, mM, 1 thousandth of a molar), micromolar (μmol/L, μM, 1 millionth of a molar) or nanomolar (nmol/L, nM, 1 billionth of a molar).

Although molarity is by far the most commonly used measure of concentration, particularly for dilute aqueous solutions, it does suffer from a number of disadvantages. Masses can be determined with great precision as balances are often very precise. Determining volume is often not as precise. In addition, due to a thermal expansion, molarity of a solution changes with temperature without adding or removing any mass.^[2] For non-dilute solutions another problem is the molar volume of a substance is itself a function of concentration so volume is not strictly additive.

Molality

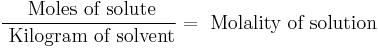
Molality (mol/kg, molal, or m) denotes the number of moles of solute per kilogram of solvent (not solution). For instance: adding 1.0 mole of solute to 2.0 kilograms of solvent constitutes a solution with a molality of 0.50 mol/kg. Such a solution may be described as "0.50 molal". The term molal solution is used as a shorthand for a "one molal solution", i.e. a solution which contains one mole of the solute per 1000 grams of the solvent.

Following the SI system of units, the National Institute of Standards and Technology, the United States authority on measurement, considers the unit symbol m to be obsolete, and suggests instead the term 'molality of substance B' (m_B) with units mol/kg or a related unit of the SI^[3]. This recommendation has not been universally implemented in academia yet.

Note: molality is sometimes represented by the symbol (m), while molarity by the symbol (M). The two symbols are not to be confused, and should not be used as symbols for units. The SI unit for molality is mol/kg. (The unit m means meter.)

Like other mass-based measures, the determination of molality only requires a good scale, because masses of both solvent and solute can be obtained by weighing, and molality is independent of physical conditions like temperature and pressure, providing advantages over molarity.

In a dilute aqueous solution near room temperature and standard atmospheric pressure, molarity and molality will be very similar in value. This is because 1 kg of water roughly corresponds to a volume of 1 L at these conditions, and because the solution is dilute, the addition of the solute makes a negligible impact on the volume of the solution.

However, in all other conditions, this is usually not the case.

Mole fraction

The mole fraction Χ, (also called molar fraction) denotes the number of moles of solute as a proportion of the total number of moles in a solution. For instance: 1 mole of solute dissolved in 9 moles of solvent has a mole fraction of 1/10 or 0.1. Mole fractions are dimensionless quantities. (The mole percentage or molar percentage, denoted "mol %" and equal to 100% times the mole fraction, is sometimes quoted instead of the mole fraction.)

This measure is used very frequently in the construction of phase diagrams. It has a number of advantages:

• the measure is not temperature dependent (such as molarity) and does not require knowledge of the densities of the phase(s) involved
• a mixture of known mole fraction can be prepared by weighing off the appropriate masses of the constituents
• the measure is symmetrical: in the mole fractions Χ=0.1 and Χ=0.9, the roles of 'solvent' and 'solute' are reversed.

As both mole fractions and molality are only based on the masses of the components it is easy to convert between these measures. This is not true for molarity, which requires knowledge of the density.

Mass percentage (fraction)

Mass percentage denotes the mass of a substance in a mixture as a percentage of the mass of the entire mixture. (Mass fraction w can be used instead of mass percentage by dividing mass percentage to 100.) Commercial concentrated aqueous reagents such as acids and bases are often labeled in concentrations of weight percentage with the specific gravity also listed. In older texts and references this is sometimes referred to as weight-weight percentage (abbreviated as w/w% ^[4] or wt%). In water pollution chemistry, a common term of measuring total mass percentage of dissolved solids in an aqueous medium is total dissolved solids.

For instance: if a bottle contains 40 grams of ethanol and 60 grams of water, then it contains 40% ethanol by mass or 0.4 mass fraction ethanol. Note that the total weight of the solution will be 100 grams, but the total volume of the solution will be less than 100 milliliters because ethanol is miscible with water.

Mass-volume percentage

Mass-volume percentage, (sometimes referred to as weight-volume percentage or percent weight per volume and often abbreviated as % m/v or % w/v) describes the mass of the solute in g per 100 mL of the resulting solution. Mass-volume percentage is often used for solutions made from a solid solute dissolved in a liquid. For example, a 40% w/v sugar solution contains 40 g of sugar per 100 mL of resulting solution.

Volume-volume percentage

Volume-volume percentage (sometimes referred to as percent volume per volume and abbreviated as % v/v) describes the volume of the solute in mL per 100 mL of the resulting solution. This is most useful when a liquid - liquid solution is being prepared, although it is used for mixtures of gases as well. For example, a 40% v/v ethanol solution contains 40 mL ethanol per 100 mL total volume. The percentages are only additive in the case of mixtures of ideal gases.

Normality

Normality highlights the chemical nature of salts: in solution, salts dissociate into distinct reactive species (ions such as H⁺, Fe³⁺, or Cl^-). Normality accounts for any discrepancy between the concentrations of the various ionic species in a solution. For example, in a salt such as MgCl₂, there are two moles of Cl^- for every mole of Mg²⁺, so the concentration of Cl^- is said to be 2 N (read: "two normal"). Further examples are given below. It may also refer to the concentration of a solute in any solution. The normality of a solution is the number of gram equivalent weight of a solute per liter of its solution. The definition of normality depends on the exact reaction intended.

For example, hydrochloric acid (HCl) is a monoprotic acid and thus has 1 mol = 1 gram equivalent. One liter of 1 M aqueous solution of HCl acid contains 36.5 grams HCl. It is called 1 N (one normal) solution of HCl. It is given by the following formula:

In contrast, for sulfuric acid, which is diprotic acid, 2 N is usually 1 M, but may be defined as 2 M if pH < 2, where the once-deprotonated species, hydrogen sulfate, does not deprotonate.

Definition

A normal is one gram equivalent of 5 solutes per liter of solution. The definition of a gram equivalent varies depending on the type of chemical reaction that is discussed in integers — it can refer to equations, bases, redox species, and ions that will precipitate and also isotopes.

Usage

It is critical to note that normality measures a single ion which takes part in an overall solute. For example, one could determine the normality of hydroxide or sodium in an aqueous solution of sodium hydroxide, but the normality of sodium hydroxide itself has no meaning. Nevertheless it is often used to describe solutions of acids or bases, in those cases it is implied that the normality refers to the H⁺ or OH⁻ ion. For example, 2 Normal sulfuric acid (H₂SO₄), means that the normality of H⁺ ions is 2, or that the molarity of the sulfuric acid is 1. Similarly for 1 molar H₃PO₄ the normality is 3 as it contains three moles of H⁺ ions for every mole of PO₄^3- .

Specific cases

As ions in solution can react through different pathways, there are three common definitions for normality as a measure of reactive species in solution:

• In acid-base chemistry, normality is used to express the concentration of protons or hydroxide ions in the solution. Here, the normality differs from the molarity by an integer value - each solute can produce n equivalents of reactive species when dissolved. For example: 1 M aqueous Ca(OH)₂ is 2 N (normal) in hydroxide.
• In redox reactions, normality measures the quantity of oxidizing or reducing agent that can accept or furnish one mole of electrons. Here, the normality scales from the molarity, most commonly, by a fractional value. Calculating the normality of redox species in solution can be challenging.
• In precipitation reactions, normality measures the concentration of ions which will precipitate in a given reaction. Here, the normality scales from the molarity again by an integer value.

Practical uses

The measure of normality is extremely useful for titrations — given two species that are known to react with a known ratio, one simply needs to scale the volumes of solutions with known normalities to get a complete reaction with the following equation:

N_aV_a=N_bV_b

However, normality cannot reliably represent an unambiguous measure of the concentration of a solution. Since the measure of normality depends on the reaction that the solute participates in, the same concentration of solute can possess two different normalities for two different reactions. For example, Mg²⁺ is 2 N with respect to a Cl^- ion, but it is only 1 N with respect to an O^2- ion.

Accordingly, normality is no longer used to represent the concentration of a solution as such. Instead, a solution should be labeled according to its molarity, and it is then possible to calculate the normality for a particular titration using the equation above. NIST has also stipulated that this unit is obsolete and recommends discontinuing its use.

Equivalents

Expression of concentration in equivalents per liter (or more commonly, milliequivalents per liter) is based on the same principle as normality. A normal solution is one equivalent per liter of solution (Eq/L). The use of equivalents and milliequivalents as a means of expressing concentration is losing favor, but medical reporting of serum concentrations in mEq/L still occurs.

Formal

The formal (F) is yet another measure of concentration similar to molarity. Formal concentrations are sometimes used when solving chemical equilibrium problems. It is calculated based on the formula weights of chemicals per liter of solution. The difference between formal and molar concentrations is that the formal concentration indicates moles of the original chemical formula in solution, without regard for the species that actually exist in solution. Molar concentration, on the other hand, is the concentration of species in solution.

For example: if one dissolves sodium carbonate (Na₂CO₃) in a liter of water, the compound dissociates into the Na⁺ and CO₃^2- ions. Some of the CO₃^2- reacts with the water to form HCO₃^- and H₂CO₃. If the pH of the solution is low, there is practically no Na₂CO₃ left in the solution. So, although we have added 1 mol of Na₂CO₃ to the solution, it does not contain 1 M of that substance. (Rather, it contains a molarity based on the other constituents of the solution.) However, it was once said that such solutions contain 1 F of Na₂CO₃.

"Parts-per" notation

The parts-per notation is used in some areas of science and engineering because it does not require conversion from weights or volumes to more chemically relevant units such as normality or molarity. It describes the amount of one substance in another, and is thus related to the mass fraction. It is the ratio of the amount of the substance of interest to the amount of that substance plus the amount of the substance it is in.

• Parts per hundred (denoted by '%' [the per cent symbol], and very rarely 'pph') - denotes the amount of a given substance in a total amount of 100 regardless of the units of measure as long as they are the same. e.g. 1 gram per 100 gram. 1 part in 10².

• Parts per thousand (denoted by '‰' [the per mille symbol], and occasionally 'ppt', but this usage can be confusing because it more often denotes parts per trillion) denotes the amount of a given substance in a total amount of 1000 regardless of the units of measure as long as they are the same. e.g. 1 milligram per gram, or 1 gram per kilogram. 1 part in 10³.

• Parts per million ('ppm') denotes the amount of a given substance in a total amount of 1,000,000 regardless of the units of measure used as long as they are the same. e.g. 1 milligram per kilogram. 1 part in 10⁶.

• Parts per billion ('ppb') denotes the amount of a given substance in a total amount of 1,000,000,000 regardless of the units of measure as long as they are the same. e.g. 1 milligram per tonne. 1 part in 10⁹.

• Parts per trillion ('ppt') denotes the amount of a given substance in a total amount of 1,000,000,000,000 regardless of the units of measure as long as they are the same. e.g. 1 milligram per kilotonne. 1 part in 10¹².

• Parts per quadrillion ('ppq') denotes the amount of a given substance in a total amount of 1,000,000,000,000,000 regardless of the units of measure as long as they are the same. e.g. 1 milligram per megatonne. 1 part in 10¹⁵.

Notes for clarity

The notation is used for convenience and the units of measure must be denoted for clarity though this is frequently not the case even in technical publications.

In atmospheric chemistry and in air pollution regulations, the parts per notation is commonly expressed with a v following, such as ppmv, to indicate parts per million by volume. This works fine for gas concentrations (e.g., ppmv of carbon dioxide in the ambient air) but, for concentrations of non-gaseous substances such as aerosols, cloud droplets, and particulate matter in the ambient air, the concentrations are commonly expressed as μg/m³ or mg/m³ (e.g., μg or mg of particulates per cubic metre of ambient air). This expression eliminates the need to take into account the impact of temperature and pressure on the density and hence weight of the gas.

The usage is generally quite fixed inside most specific branches of science, leading some researchers to believe that their own usage (mass/mass, volume/volume or others) is the only correct one. This, in turn, leads them not to specify their usage in their research, and others may therefore misinterpret their results. For example, electrochemists often use volume/volume, while chemical engineers may use mass/mass as well as volume/volume. Many academic papers of otherwise excellent level fail to specify their usage of the part-per notation. The difference between expressing concentrations as mass/mass or volume/volume is quite significant when dealing with gases and it is very important to specify which is being used. It is quite simple, for example, to distinguish ppm by volume from ppm by mass or weight by using ppmv or ppmw.

Table of concentration measures

Frequently used standards of concentration

Measurement	Notation	Generic formula	Typical units
atomic percentage (A)	at.%		%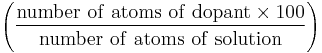
atomic percentage (B)	at.%		%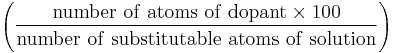
Mass percentage	wt%		%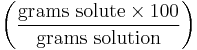
Mass-volume percentage	-		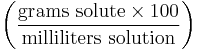% though strictly %g/mL
Volume-volume percentage	vol%		%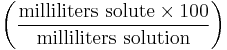
Molarity	M		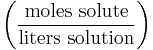mol/L (or M or mol/dm3)
Molinity	-		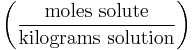mol/kg
Molality	m		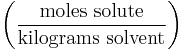mol/kg (or m**)
Molar fraction	χ (chi)		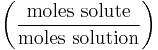(decimal)
Formal	F		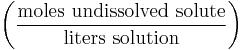mol/L (or F)
Normality	N		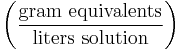N
Parts per hundred	% (or pph)		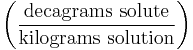dg/kg
Parts per thousand	‰ (or ppt*)		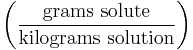g/kg
Parts per million	ppm		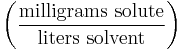mg/L
Parts per billion	ppb		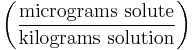µg/kg
Parts per trillion	ppt*		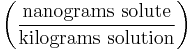ng/kg
Parts per quadrillion	ppq		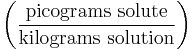pg/kg

* Although 'ppt' is usually used to denote 'parts per trillion', it is on occasion used for 'parts per thousand'. Sometimes 'ppt' is also used as an abbreviation for precipitate.

** Obsolete unit symbols.

See also

• Chemical equilibrium
• Serial dilution
• formulations for fundamentals, manipulation and datamanagement of % in a formulation

References