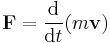Mechanics

Mechanics (Greek Μηχανική) is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment. The discipline has its roots in several ancient civilizations (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo, Kepler, and especially Newton, laid the foundation for what is now known as classical mechanics.

The system of study of mechanics is shown in the table below:

Branches of mechanics

Contents

Classical versus quantum

Classical mechanics
History of classical mechanics · Timeline of classical mechanics
Branches
Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics
Quantum mechanics
\Delta x\, \Delta p \ge \frac{\hbar}{2}
Uncertainty principle
Introduction · Mathematical formulations

The major division of the mechanics discipline separates classical mechanics from quantum mechanics.

Historically, classical mechanics came first, while quantum mechanics is a comparatively recent invention. Classical mechanics originated with Isaac Newton's Laws of motion in Principia Mathematica, while quantum mechanics didn't appear until 1900. Both are commonly held to constitute the most certain knowledge that exists about physical nature. Classical mechanics has especially often been viewed as a model for other so-called exact sciences. Essential in this respect is the relentless use of mathematics in theories, as well as the decisive role played by experiment in generating and testing them.

Quantum mechanics is of a wider scope, as it encompasses classical mechanics as a sub-discipline which applies under certain restricted circumstances. According to the correspondence principle, there is no contradiction or conflict between the two subjects, each simply pertains to specific situations. The correspondence principle states that the behavior of systems described by quantum theories reproduces classical physics in the limit of large quantum numbers. Quantum mechanics has superseded classical mechanics at the foundational level and is indispensable for the explanation and prediction of processes at molecular and (sub)atomic level. However, for macroscopic processes classical mechanics is able to solve problems which are unmanageably difficult in quantum mechanics and hence remains useful and well used.

Einsteinian versus Newtonian

Analogous to the quantum versus classical reformation, Einstein's general and special theories of relativity have expanded the scope of mechanics beyond the mechanics of Newton and Galileo, and made fundamental corrections to them, that become significant and even dominant as speeds of material objects approach the speed of light, which cannot be exceeded. Relativistic corrections are also needed for quantum mechanics, although General relativity has not been integrated; the two theories remain incompatible, a hurdle which must be overcome in developing the Grand Unified Theory.

History

Antiquity

The main theory of mechanics in antiquity was Aristotelian mechanics.[1] A later developer in this tradition was Hipparchus.[2]

Medieval age

In the Middle Ages, Aristotle's theories were criticized and modified by a number of figures, beginning with John Philoponus in the 6th century, and reaching its peak during the Golden Age of Islam. A central problem was that of projectile motion, which was discussed by Hipparchus and Philoponus. This led to the development of the theory of impetus by 14th century French Jean Buridan, which developed into the modern theories of inertia, velocity, acceleration and momentum. This work and others was developed in 14th century England by the Oxford Calculators such as Thomas Bradwardine, who studied and formulated various laws regarding falling bodies.

On the question of a body subject to a constant (uniform) force, the 12th century Jewish-Arab Nathanel (Iraqi, of Baghdad) stated that constant force imparts constant acceleration, while the main properties are uniformly accelerated motion (as of falling bodies) was worked out by the 14th century Oxford Calculators.

Early modern age

Two central figures in the early modern age are Galileo Galilei and Isaac Newton. Galileo's final statement of his mechanics, particularly of falling bodies, is his Two New Sciences (1638). Newton's 1687 Philosophiæ Naturalis Principia Mathematica provided a detailed mathematical account of mechanics, using the newly developed mathematics of calculus and providing the basis of Newtonian mechanics.[2]

There is some dispute over priority of various ideas: Newton's Principia is certainly the seminal work and has been tremendously influential, and the systematic mathematics therein did not and could not have been stated earlier because calculus had not been developed. However, many of the ideas, particularly as pertain to inertia (impetus) and falling bodies had been developed and stated by earlier researchers, both the then-recent Galileo and the less-known medieval predecessors. Precise credit is at times difficult or contentious because scientific language and standards of proof changed, so whether medieval statements are equivalent to modern statements or sufficient proof, or instead similar to modern statements and hypotheses is often debatable.

Modern age

Two main modern developments in mechanics are general relativity of Einstein, and quantum mechanics, both developed in the 20th century based in part on earlier 19th century ideas.

Types of mechanical bodies

Thus the often-used term body needs to stand for a wide assortment of objects, including particles, projectiles, spacecraft, stars, parts of machinery, parts of solids, parts of fluids (gases and liquids), etc.

Other distinctions between the various sub-disciplines of mechanics, concern the nature of the bodies being described. Particles are bodies with little (known) internal structure, treated as mathematical points in classical mechanics. Rigid bodies have size and shape, but retain a simplicity close to that of the particle, adding just a few so-called degrees of freedom, such as orientation in space.

Otherwise, bodies may be semi-rigid, i.e. elastic, or non-rigid, i.e. fluid. These subjects have both classical and quantum divisions of study.

For instance, the motion of a spacecraft, regarding its orbit and attitude (rotation), is described by the relativistic theory of classical mechanics, while the analogous movements of an atomic nucleus are described by quantum mechanics.

Sub-disciplines in mechanics

The following are two lists of various subjects that are studied in mechanics.

Note that there is also the "theory of fields" which constitutes a separate discipline in physics, formally treated as distinct from mechanics, whether classical fields or quantum fields. But in actual practice, subjects belonging to mechanics and fields are closely interwoven. Thus, for instance, forces that act on particles are frequently derived from fields (electromagnetic or gravitational), and particles generate fields by acting as sources. In fact, in quantum mechanics, particles themselves are fields, as described theoretically by the wave function.

Classical mechanics

The following are described as forming Classical mechanics:

Quantum mechanics

The following are categorized as being part of Quantum mechanics:

Professional organizations

See also

References

  1. ↑ "A history of mechanics". René Dugas (1988). p.19. ISBN 0486656322
  2. ↑ 2.0 2.1 "A Tiny Taste of the History of Mechanics". The University of Texas at Austin.

Further reading

External links