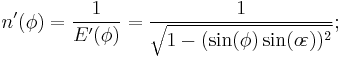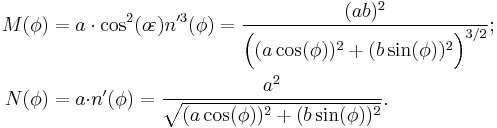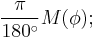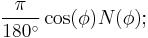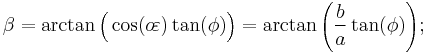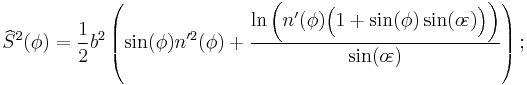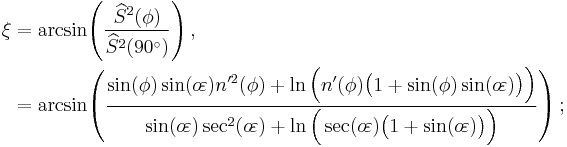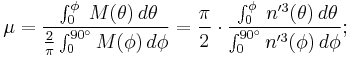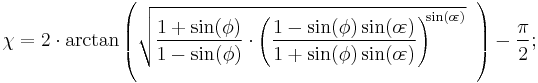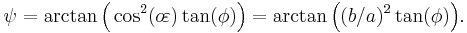Latitude
Latitude, usually denoted by the Greek letter phi (φ) gives the location of a place on Earth (or other planetary body) north or south of the equator. Lines of Latitude are the imaginary horizontal lines shown running east-to-west (or west to east) on maps (particularly so in the Mercator projection) that run either north or south of the equator. Technically, latitude is an angular measurement in degrees (marked with °) ranging from 0° at the equator (low latitude) to 90° at the poles (90° N or +90° for the North Pole and 90° S or −90° for the South Pole). The latitude is approximately the angle between straight up at the surface (the zenith) and the noonday sun when it is at the equinox. The complementary angle of a latitude is called the colatitude.
 |
|
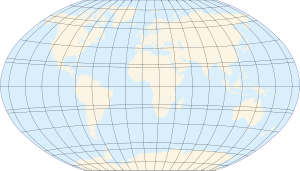
| Map of Earth | |
| Longitude (λ) | |
|---|---|
| Lines of longitude appear vertical with varying curvature in this projection, but are actually halves of great ellipses, with identical radii at a given latitude. | |
| Latitude (φ) | |
| Lines of latitude appear horizontal with varying curvature in this projection; but are actually circular with different radii. All locations with a given latitude are collectively referred to as a circle of latitude. | |
| The equator divides the planet into a Northern Hemisphere, a Southern Hemisphere and has a latitude of 0°. | |
Contents |
Circles of latitude
All locations of a given latitude are collectively referred to as a circle of latitude or line of latitude or parallel, because they are coplanar, and all such planes are parallel to the equator. Lines of latitude other than the Equator are approximately small circles on the surface of the Earth; they are not geodesics since the shortest route between two points at the same latitude is a path that (when drawn on most small-scale maps) seems to bulge toward the nearest pole, first moving farther away from and then back toward the equator (see great circle).

A specific latitude may then be combined with a specific longitude to give a precise position on the Earth's surface (see satellite navigation system).
Important named circles of latitude
Besides the equator, four other lines of latitude are named because of the role they play in the geometrical relationship with the Earth and the Sun:
- Arctic Circle: 66° 33′ 39″ N
- Tropic of Cancer: 23° 26′ 21″ N
- Equator: 0° Latitude
- Tropic of Capricorn: 23° 26′ 21″ S
- Antarctic Circle: 66° 33′ 39" S
Only at latitudes between the Tropics is it possible for the sun to be at the zenith. Only north of the Arctic Circle or south of the Antarctic Circle is the midnight sun possible. The reason that these lines have the values that they do lies in the axial tilt of the Earth with respect to the sun, which is 23° 26′ 21.41″.
The Arctic Circle and Tropic of Cancer are colatitudes, since the sum of their angles is 90° — similarly for the Antarctic Circle and Tropic of Capricorn.
Subdivisions
A degree is divided into 60 minutes. One minute can be further divided into 60 seconds. An example of a latitude specified in this way is 13°19'43″ N (for greater precision, a decimal fraction can be added to the seconds). An alternative representation uses only degrees and minutes, where the seconds are expressed as a decimal fraction of minutes: the above example would be expressed as 13°19.717' N. Degrees can also be expressed singularly, with both the minutes and seconds incorporated as a decimal number and rounded as desired (decimal degree notation): 13.32861° N. Sometimes, the north/south suffix is replaced by a negative sign for south (−90° for the South Pole).
Effect of latitude

A region's latitude has a great effect on its climate and weather. Latitude more loosely determines prevailing winds, and other physical characteristics of geographic locations. Auroral activity is common at high geomagnetic latitudes.
Some observers have noted a correlation between the latitude of a country and its economic activity; see North-South divide.
Elliptic parameters
Because most planets (including Earth) are ellipsoids of revolution, or spheroids, rather than spheres, both the radius and the length of arc varies with latitude. This variation requires the introduction of elliptic parameters based on an ellipse's angular eccentricity, 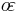 (which equals
(which equals 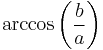 , where
, where 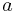 and
and 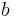 are the equatorial radius (6378137.0 m for Earth) and the polar radius (6356752.3142 m for Earth), respectively;
are the equatorial radius (6378137.0 m for Earth) and the polar radius (6356752.3142 m for Earth), respectively; 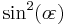 is the first eccentricity squared,
is the first eccentricity squared, 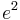 ; and
; and 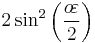 or
or 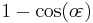 is the flattening,
is the flattening, 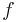 . Utilized in creating the integrands for curvature is the inverse of the principal elliptic integrand,
. Utilized in creating the integrands for curvature is the inverse of the principal elliptic integrand, 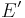 :
:
Degree length
On Earth, the length of an arcdegree of north–south latitude difference, 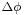 , is about 60 nautical miles, 111 kilometres or 69 statute miles at any latitude. The length of an arcdegree of east-west longitude difference,
, is about 60 nautical miles, 111 kilometres or 69 statute miles at any latitude. The length of an arcdegree of east-west longitude difference, 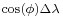 , is about the same at the equator as the north-south, reducing to zero at the poles.
, is about the same at the equator as the north-south, reducing to zero at the poles.
In the case of a spheroid, a meridian and its anti-meridian form an ellipse, from which an expression for the length of an arcdegree of latitude difference is:
This radius of arc (or "arcradius") is in the plane of a meridian, and is known as the meridional radius of curvature, 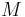 .[1][2]
.[1][2]
Similarly, an expression for the length of an arcdegree of longitude difference is:
The arcradius contained here is in the plane of the prime vertical, the east-west plane perpendicular (or "normal") to both the plane of the meridian and the plane tangent to the surface of the ellipsoid, and is known as the normal radius of curvature, 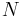 .[1][2]
.[1][2]
Along the equator (east-west), 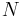 equals the equatorial radius. The radius of curvature at a right angle to the equator (north-south),
equals the equatorial radius. The radius of curvature at a right angle to the equator (north-south), 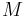 , is 43 km shorter, hence the length of an arcdegree of latitude difference at the equator is about 1 km less than the length of an arcdegree of longitude difference at the equator. The radii of curvature are equal at the poles where they are about 64 km greater than the north-south equatorial radius of curvature because the polar radius is 21 km less than the equatorial radius. The shorter polar radii indicate that the northern and southern hemispheres are flatter, making their radii of curvature longer. This flattening also 'pinches' the north-south equatorial radius of curvature, making it 43 km less than the equatorial radius. Both radii of curvature are perpendicular to the plane tangent to the surface of the ellipsoid at all latitudes, directed toward a point on the polar axis in the opposite hemisphere (except at the equator where both point toward Earth's center). The east-west radius of curvature reaches the axis, whereas the north-south radius of curvature is shorter at all latitudes except the poles.
, is 43 km shorter, hence the length of an arcdegree of latitude difference at the equator is about 1 km less than the length of an arcdegree of longitude difference at the equator. The radii of curvature are equal at the poles where they are about 64 km greater than the north-south equatorial radius of curvature because the polar radius is 21 km less than the equatorial radius. The shorter polar radii indicate that the northern and southern hemispheres are flatter, making their radii of curvature longer. This flattening also 'pinches' the north-south equatorial radius of curvature, making it 43 km less than the equatorial radius. Both radii of curvature are perpendicular to the plane tangent to the surface of the ellipsoid at all latitudes, directed toward a point on the polar axis in the opposite hemisphere (except at the equator where both point toward Earth's center). The east-west radius of curvature reaches the axis, whereas the north-south radius of curvature is shorter at all latitudes except the poles.
The WGS84 ellipsoid, used by all GPS devices, uses an equatorial radius of 6378137.0m and an inverse flattening, (1/f), of 298.257223563, hence its polar semi-axis is 6356752.3142m and its first eccentricity squared is 0.00669437999014.[3] The more recent but little used IERS 2003 ellipsoid provides equatorial and polar semi-axes of 6378136.6 and 6356751.9m, respectively, and an inverse flattening of 298.25642.[4] Lengths of degrees on the WGS84 and IERS 2003 ellipsoids are the same when rounded to six significant digits. An appropriate calculator for any latitude is provided by the U.S. government's National Geospatial-Intelligence Agency (NGA).[5]
| Latitude | N-S radius of curvature 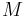 |
Surface distance per 1° change in latitude |
E-W radius of curvature 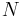 |
Surface distance per 1° change in longitude |
|
|---|---|---|---|---|---|
| 0° | 6335.44 km | 110.574 km | 6378.14 km | 111.320 km | |
| 15° | 6339.70 km | 110.649 km | 6379.57 km | 107.551 km | |
| 30° | 6351.38 km | 110.852 km | 6383.48 km | 96.486 km | |
| 45° | 6367.38 km | 111.132 km | 6388.84 km | 78.847 km | |
| 60° | 6383.45 km | 111.412 km | 6394.21 km | 55.800 km | |
| 75° | 6395.26 km | 111.618 km | 6398.15 km | 28.902 km | |
| 90° | 6399.59 km | 111.694 km | 6399.59 km | 0.000 km |
Types of latitude
With a spheroid that is slightly flattened by its rotation, cartographers refer to a variety of auxiliary latitudes to precisely adapt spherical projections according to their purpose.
For planets other than Earth, such as Mars, geographic and geocentric latitude are called "planetographic" and "planetocentric" latitude, respectively. Most maps of Mars since 2002 use planetocentric coordinates.
Common "latitude"
In common usage, "latitude" at a point refers to its geodetic or geographic latitude 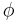 and is the angle between the equatorial plane and a line through the point that is normal to the reference ellipsoid, the slightly-squashed sphere chosen to approximate the shape of the sea-level surface of the earth. This value differs from the geocentric latitude, except that both are 0 at the equator and both are 90 degrees at the pole.
and is the angle between the equatorial plane and a line through the point that is normal to the reference ellipsoid, the slightly-squashed sphere chosen to approximate the shape of the sea-level surface of the earth. This value differs from the geocentric latitude, except that both are 0 at the equator and both are 90 degrees at the pole.
The expressions following assume elliptical polar sections and that all sections parallel to the equatorial plane are circular. Geographic latitude (with longitude) then provides a Gauss map. As defined earlier in this article, 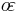 is the angular eccentricity of a meridian.
is the angular eccentricity of a meridian.
Reduced latitude
- On a spheroid, lines of reduced or parametric latitude,
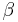 , form circles whose radii are the same as the radii of circles formed by the corresponding lines of latitude on a sphere with radius equal to the equatorial radius of the spheroid.
, form circles whose radii are the same as the radii of circles formed by the corresponding lines of latitude on a sphere with radius equal to the equatorial radius of the spheroid.
- Envision a sphere superimposed on the spheroid, with the two equators coinciding. A line perpendicular to their common equatorial plane passes thru the surface of each, intersecting the spheroid at latitude
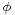 ; the point where it intersects the sphere has latitude
; the point where it intersects the sphere has latitude 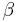 on the sphere, where
on the sphere, where 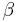 is the reduced latitude corresponding to
is the reduced latitude corresponding to 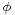 .
.
- It follows that the radius of a parallel of latitude on the spheroid is
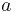 times
times 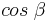 exactly (i.e. the radius of the parallel of latitude
exactly (i.e. the radius of the parallel of latitude 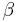 on the sphere of radius
on the sphere of radius 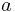 ).
).
Authalic latitude
- Authalic latitude,
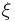 , gives an area-preserving transform to the sphere.
, gives an area-preserving transform to the sphere.
Rectifying latitude
- Rectifying latitude,
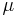 , is the surface distance from the equator, scaled so the pole is 90°, but involves elliptic integration:
, is the surface distance from the equator, scaled so the pole is 90°, but involves elliptic integration:
Conformal latitude
- Conformal latitude,
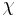 , gives an angle-preserving (conformal) transform to the sphere.
, gives an angle-preserving (conformal) transform to the sphere.
Geocentric latitude
- The geocentric latitude,
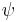 , is the angle between the equatorial plane and a line from the center of Earth.
, is the angle between the equatorial plane and a line from the center of Earth.
-
- It is the size of the central angle between the equator and the point of interest, as measured along a meridian. Except at the equator and at the pole, this value differs from the geographic latitude, as so:

Astronomical latitude
A fundamentally different measure of latitude is the astronomical latitude, which is the angle between the equatorial plane and the normal to the geoid (i.e. a plumb line). This is the only "latitude" that is not based on the spheroid being used to approximate the earth's surface. It differs from the geodetic latitude only slightly (usually not more than a few thousandths of a degree) due to the slight deviations of the geoid from the reference ellipsoid.
Astronomical latitude is not to be confused with declination, the coordinate astronomers use to describe the locations of stars north/south of the celestial equator (see equatorial coordinates), nor with ecliptic latitude, the coordinate that astronomers use to describe the locations of stars north/south of the ecliptic (see ecliptic coordinates).
Paleolatitude
Continents move over time, due to continental drift, taking whatever fossils and other features of interest they may have with them. Particularly when discussing fossils, it is often more useful to know where the fossil was when it was laid down, than where it is when it was dug up: this is called the paleolatitude of the fossil. The Paleolatitude can be constrained by paleomagnetic data. If tiny magnetisable grains are present when the rock is being formed, these will align themselves with Earth's magnetic field like compass needles. A magnetometer can deduce the orientation of these grains by subjecting a sample to a magnetic field, and the magnetic declination of the grains can be used to infer the latitude of deposition.
Comparison of selected types
The following plot shows the differences between the types of latitude. The data used are found in the table following the plot. Please note that the values in the table are in minutes, not degrees, and the plot reflects this as well. Also observe that the conformal symbols are hidden behind the geocentric due to being very close in value. Finally it is important to mention also that these differences don't mean that the use of one specific latitude will necessarily cause more distortions than the other (the real fact is that each latitude type is optimized for achieving a different goal).
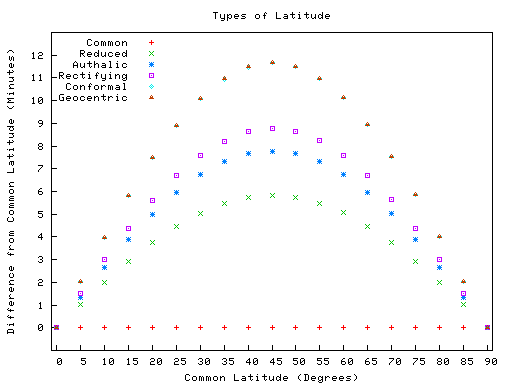
-
Approximate difference from geographic latitude ("Lat") Lat
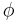
Reduced
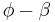
Authalic
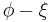
Rectifying
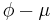
Conformal
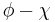
Geocentric
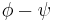
0° 0.00′ 0.00′ 0.00′ 0.00′ 0.00′ 5° 1.01′ 1.35′ 1.52′ 2.02′ 2.02′ 10° 1.99′ 2.66′ 2.99′ 3.98′ 3.98′ 15° 2.91′ 3.89′ 4.37′ 5.82′ 5.82′ 20° 3.75′ 5.00′ 5.62′ 7.48′ 7.48′ 25° 4.47′ 5.96′ 6.70′ 8.92′ 8.92′ 30° 5.05′ 6.73′ 7.57′ 10.09′ 10.09′ 35° 5.48′ 7.31′ 8.22′ 10.95′ 10.96′ 40° 5.75′ 7.66′ 8.62′ 11.48′ 11.49′ 45° 5.84′ 7.78′ 8.76′ 11.67′ 11.67′ 50° 5.75′ 7.67′ 8.63′ 11.50′ 11.50′ 55° 5.49′ 7.32′ 8.23′ 10.97′ 10.98′ 60° 5.06′ 6.75′ 7.59′ 10.12′ 10.13′ 65° 4.48′ 5.97′ 6.72′ 8.95′ 8.96′ 70° 3.76′ 5.01′ 5.64′ 7.52′ 7.52′ 75° 2.92′ 3.90′ 4.39′ 5.85′ 5.85′ 80° 2.00′ 2.67′ 3.00′ 4.00′ 4.01′ 85° 1.02′ 1.35′ 1.52′ 2.03′ 2.03′ 90° 0.00′ 0.00′ 0.00′ 0.00′ 0.00′
Corrections for altitude

When converting from geodetic ("common") latitude to other types of latitude, corrections must be made for altitude for systems which do not measure the angle from the normal of the spheroid. For example, in the figure at right, point H (located on the surface of the spheroid) and point H' (located at some greater elevation) have different geocentric latitudes (angles β and γ respectively), even though they share the same geodetic latitude (angle α). Note that the flatness of the spheroid and elevation of point H' in the image is significantly greater than what is found on the Earth, exaggerating the errors inherent in such calculations if left uncorrected. Note also that the reference ellipsoid used in the geodetic system is itself just an approximation of the true geoid, and therefore introduces its own errors, though the differences are less severe. (See Astronomical latitude, above.)
See also
- American Practical Navigator
- Cardinal direction
- Geographic coordinate system
- Geodetic system
- Geodesy
- Geographical distance
- Geotagging
- Great-circle distance
- Horse latitudes
- List of cities by latitude
- List of cities by longitude
- Longitude
- Natural Area Code
- Navigation
- World Geodetic System
- Orders of magnitude (length)
Footnotes
- ↑ 1.0 1.1 The Math Forum
- ↑ 2.0 2.1 John P. Snyder, Map Projections: A Working Manual (1987) 24-25
- ↑ NIMA TR8350.2 page 3-1.
- ↑ IERS Conventions (2003) (Chp. 1, page 12)
- ↑ Length of degree calculator - National Geospatial-Intelligence Agency
External links
- A Comprehensive Library of Cartographic Projection Functions (Preliminary Draft) at the Internet ArchivePDF (1.88 MB)
- GEONets Names Server, access to the National Geospatial-Intelligence Agency's (NGA) database of foreign geographic feature names.
- Look-up Latitude and Longitude
- Resources for determining your latitude and longitude
- Convert decimal degrees into degrees, minutes, seconds - Info about decimal to sexagesimal conversion
- Convert decimal degrees into degrees, minutes, seconds
- Latitude and longitude converter – Convert latitude and longitude from degree, decimal form to degree, minutes, seconds form and vice versa. Also included a farthest point and a distance calculator.
- Distance calculation based on latitude and longitude - JavaScript version
- Zoomable version of the mapPDF (3.47 MB)
- Determination of Latitude by Francis Drake on the Coast of California in 1579
|
|||||